пр. Примечания Необходимо
 Скачать 20.14 Kb. Скачать 20.14 Kb.
|
|
Практические задания Примечания:Необходимо решить ВСЕ задачи. Работа должна быть оформлена в ОДНОМ файле. При загрузке работы НЕ ИСПОЛЬЗУЙТЕ архиваторы. 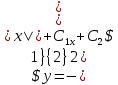 Задачи:Методом изоклин построить интегральные кривые уравнения  1.1. 𝑑𝑦 = 2𝑥(1 − 𝑦) 𝑑𝑥 Решить уравнение, допускающее понижения порядка: 𝑥2𝑦’’ = 𝑦’2 Решить систему уравнений   𝑑𝑥 = 𝑡 𝑑𝑥 = 𝑡3.1./ 𝑑𝑡 𝑦   𝑑𝑦 = − 𝑡 𝑑𝑦 = − 𝑡𝑑𝑡 𝑥 Вероятность появления события в каждом испытании равна 0,7. Сколько нужно провести испытаний, чтобы наивероятнейшее число появлений события равнялось 10? Задача №1 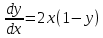 Решим уравнение методом разделения переменных: dy/(1-y) = 2x dx Проинтегрируем обе части: -ln|1-y| = x^2 + C где C - произвольная постоянная. Выразим y: 1-y = e^(-x^2 - C) y = 1 - e^(-x^2 - C) Для построения интегральных кривых заданного уравнения можно использовать метод изоклин: 1) Найдем изоклины, т.е. кривые, на которых значение произведения 2x(1-y) постоянно: 2x(1-y) = C y = 1 - x^2/C 2) Построим графики изоклин и найдем, как изменяется знак произведения 2x(1-y) на каждой из них. На тех участках изоклин, где произведение положительно, интегральные кривые должны идти вправо, на тех, где отрицательно, - влево. 3) Нарисуем на графике несколько интегральных кривых, используя полученное выражение для y. Пример построения интегральных кривых уравнения dy/dx=2x(1-y): Задача №2 Пусть $u=y'$, тогда $u'=\frac{d(u)}{dx}=\frac{d(y')}{dx}=y''$, а уравнение примет вид: $x^2 u' = u^2$ Переносим $u^2$ в левую часть: $x^2 u' - u^2 = 0$ Это уравнение Эйлера-Лагранжа, поэтому делаем замену $u=x^m$: $x^2 \cdot m x^{m-1} - x^{2m} = 0$ $x^{m+1} \cdot (m - x^m) = 0$ Получаем два уравнения: $x^{m+1}=0$ и $m-x^m=0$ Решение первого уравнения: $m=-1$, тогда $u = \frac{y'}{x}=-\frac{1}{x}$. Решение второго уравнения: $m=1$, тогда $u=x$. Перейдем обратно к $y''$: $u = y' = -\frac{1}{x},\ y'=-\ln(|x|)+C_1$ $u = y' = x,\ y=\frac{1}{2}x^2+C_2$. Ответ: $y=-\frac{1}{2}\ln^2(|x|)+C_1x+C_2$. $y=−12ln2(|x|)+C1x+C2$ Задача №3 Дана следующая система дифференциальных уравнений:  Решение: Мы можем выразить x и y через t и константы, используя методы решения дифференциальных уравнений. Дифференцируя первое уравнение по t и подставляя второе уравнение, получаем: d^2x/dt^2 = -(y/x) * dx/dt - t/y * dy/dt Заменяя dx/dt и dy/dt на их соответствующие значения, получаем: d^2x/dt^2 = -t/x * (-t/x) - t/y * (t/y) = t^2 * (1/x^2 + 1/y^2) Теперь дифференцируем второе уравнение по t и подставляем первое уравнение: d^2y/dt^2 = (-x/y) * dy/dt + t/x * dx/dt Заменяя dx/dt и dy/dt на их соответствующие значения, получаем: d^2y/dt^2 = -t/x * (-t/y) - t/y * (t/x) = 0 Таким образом, мы получили два дифференциальных уравнения. Второе уравнение говорит о том, что вторая производная y равна нулю, что означает, что y является линейной функцией от t. Поэтому мы можем записать: y = c1 + c2 * t где c1 и c2 - произвольные постоянные. Теперь мы можем перейти к первому уравнению. Подставляя y = c1 + c2 * t, получаем: dx/dt = t / (c1 + c2 * t) Сделаем замену переменных: x = u * (c1 + c2 * t) dx/dt = du/dt * (c1 + c2 * t) + u * c2 Подставляем эти выражения в первое уравнение и упрощаем: du/dt = 1 / (c1 + c2 * t)^2 Мы можем интегрировать это уравнение по t, чтобы получить u: u = -1 / (c2 * (c1 + c2 * t)) + c3 где c3 - произвольная постоянная. Теперь мы можем выразить x, используя y и u: x = u * (c1 + c2 * t) = (-1 / (c2 * (c1 + c2 * t)) + c3) * (c1 + c2 * t) Таким образом, решение этой системы дифференциальных уравнений будет выглядеть как: x = (-t + c1 / t) * (c2 + c3 * t) y = c1 + c2 * t где c1, c2 и c3 - произвольные постоянные. Задача №4 Для решения задачи необходимо использовать биномиальное распределение, которое задается формулой: P(X=k) = C(n,k) * p^k * (1-p)^(n-k) где X - число появлений события в n испытаниях, k - количество появлений события, p - вероятность появления события в каждом испытании, C(n,k) - количество сочетаний из n по k. Для наивероятнейшего числа появлений события необходимо найти такое n, при котором значение P(X=k) будет максимальным. Для этого можно воспользоваться формулой для нахождения моды биномиального распределения: mode = (n+1) * p С учетом того, что необходимо получить 10 появлений события, получим: 10 = (n+1) * 0.7 n = (10/0.7) - 1 n ≈ 13.1 Ответ: необходимо провести 14 испытаний, чтобы наивероятнейшее число появлений события равнялось 10. |
