1. Определение вероятности (классическое, статистическое, геометрическое) в классической
 Скачать 0.52 Mb.
|
|
1. Определение вероятности (классическое, статистическое, геометрическое) В классической модели вероятность любого события А равна отношению числа М случаев, благоприятствующих этому событию, к общему числу N всех случаев: 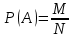 .Отношение числа появлений m события А к общему числу испытаний n называется относительной частотой события А: 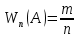 . При однотипных массовых испытаниях во многих случаях наблюдается устойчивость относительной частоты события, т. е. 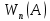при числе испытаний n относительная частота  события А колеблется около некоторого постоянного числа p, причем эти отклонения тем меньше, чем больше произведено испытаний, если не учитывать отдельные неудачные испытания. Статистической вероятностью события А называют число p, возле которого колеблется относительная частота события А при n .Геометрическая вероятность – вероятность попадания точки в область (отрезок, часть плоскости и т. д.). 2. Элементы комбинаторики (сочетание, размещение, перестановка (без схем с повторениями)) Размещениями из n элементов по m называются такие соединения, которые различаются самими элементами или их порядком. Число всех размещений из n элементов по m равно: 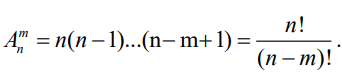 Перестановками из n элементов называются их соединения, различающиеся только порядком входящих в них элементов. Число всех перестановок из n различных элементов равно:  Сочетаниями из n элементов по m называются такие их соединения, которые различаются только своими элементами. Число сочетаний из n элементов по m равно:  3. Формула полной вероятности/Байеса (определение, ч. т. условная вероятность и т. д.) Вероятность события А при условии, что произошло событие В, называется условной вероятностью события А и обозначается: 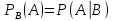 Случайные события образуют полную группу, если они попарно несовместны и, если при каждом повторении испытания должно произойти хотя бы одно из них. Пусть событие A может произойти в результате появления одного и только одного события Hi ( i 1 , 2 , ... , n )) из некоторой полной группы несовместных событий H1 , H2 , ..., H n . События этой группы обычно называются гипотезами. Вероятность события A равна сумме произведений вероятностей всех гипотез, образующих полную группу, на соответствующие условные вероятности данного события A , т. е.:  Формула выше называется формулой полной вероятности. Одно из интересных применений формулы полной вероятности связано с формулами Байеса (Бейеса). Если в выражении для условной вероятности 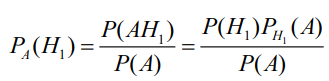 заменить вероятность P(A) по формуле полной вероятности, можно получить формулу Байеса 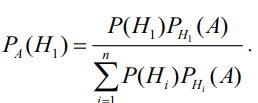 Эта формула применяется для вычисления условной вероятности PA(H1) гипотезы H1 после испытания, при котором произошло событие A. Аналогичные формулы имеют место для условных вероятностей PA(Hk) всех гипотез Hk: 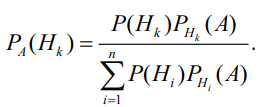 Другими словами формулы Байеса позволяют переоценить вероятности гипотез, принятые до испытания (априорные), по результатам уже произведенного испытания. 4. Схема Бернулли (формула) Два события А и В называются независимыми, если вероятность каждого из них не зависит от появления или непоявления другого. Если производится n независимых испытаний, в каждом из которых событие А появляется с вероятностью р и не появляется с вероятностью q, то вероятность наступления события А m раз в этих n испытаниях вычисляется по формуле Бернулли:  5. Предельные теоремы в схеме Бернулли (где применяются) 1) Формула Пуассона Предположим, что произведение np является постоянной величиной, когда n неограниченно возрастает. Обозначим np . Тогда для любого фиксированного :  2) Теорема Муавра-Лапласа (локальная и интегральная) Локальная теорема Муавра-Лапласа: если число испытаний велико, а вероятность наступления события отлична от 0 и 1, то вероятность наступления события m раз в n испытаниях вычисляют по формуле: 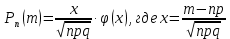 Интегральная теорема Муавра-Лапласа: если вероятность наступления события в испытаниях постоянна и отлична от 0 и 1, то вероятность того, что событие Pn(k1≤m≤k2) наступит вычисляется по формуле: 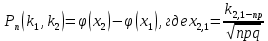 6. Определение случайной величины. Многоугольник распределения Величина называется случайной, если она принимает свои значения в зависимости от исходов некоторого испытания, причем для каждого элементарного исхода она имеет единственное значение. Графически дискретная случайная величина может быть представлена в виде многоугольника распределения 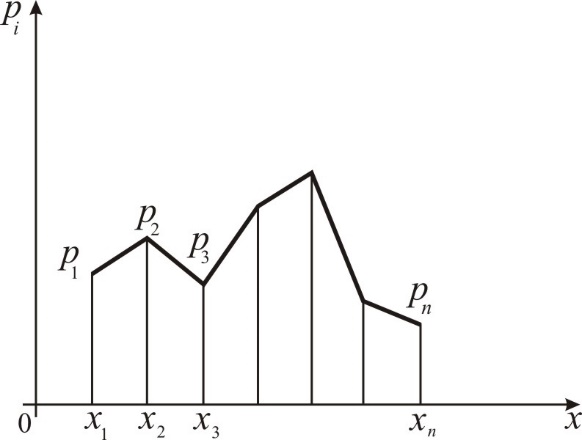 7. Функция распределения (определение и смысл), плотность распределения (как связаны), их свойства Соответствие между всеми возможными значениями дискретной случайной величины и их вероятностями называется законом распределения данной случайной величины. 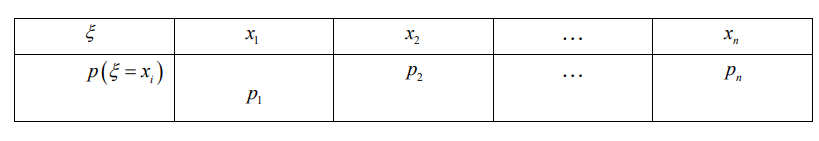 Функцией распределения случайной величины ξ называется функция:  Функцией распределения случайной величины ξ называют функцию F(x), определяющую вероятность того, что случайная величина ξ в результате испытания примет значение, меньшее x, т. е. F(x)=P(ξ Свойства функции распределения Свойство 1. F(x) – неубывающая функция. Свойство 2. F(−∞)=0, F(+∞)=1. Свойство 3. Функция F(x) непрерывна слева. Свойство 4. Для любых a  Свойство 5. 0≤F(x)≤1. Плотностью распределения случайной величины ξ называется производная от функции распределения f(x)=F′(x). Свойства плотности вероятности Свойство 1. Плотность распределения есть функция неотрицательная: f(x)≥0. Свойство 2. 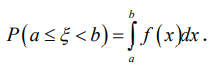 Следствие 1. 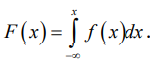 Следствие 2.  8. НСВ, ДСВ (непрерывная и дискретная случайная величина), их определение Случайная величина называется дискретной, если множество всех возможных значений ее конечно. Случайная величина называется непрерывной, если множество всех возможных значений её бесконечно. 9. Числовые характеристики: математическое ожидание, дисперсия, среднеквадратическое отклонение, мода, медиана. Нарисовать картинки Математическим ожиданием дискретной случайной величины называют сумму произведений всех её возможных значений на их вероятности: 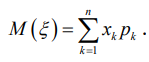 Математическое ожидание приблизительно равно среднему арифметическому наблюдаемых значений случайной величины. Математическим ожиданием непрерывной случайной величины ξ называется число: 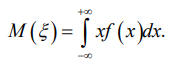 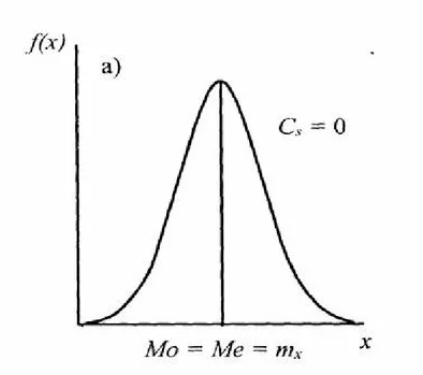 Дисперсией случайной величины ξ называется математическое ожидание квадрата отклонения случайной величины от своего математического ожидания:  Среднее квадратичное отклонение – корень из дисперсии. 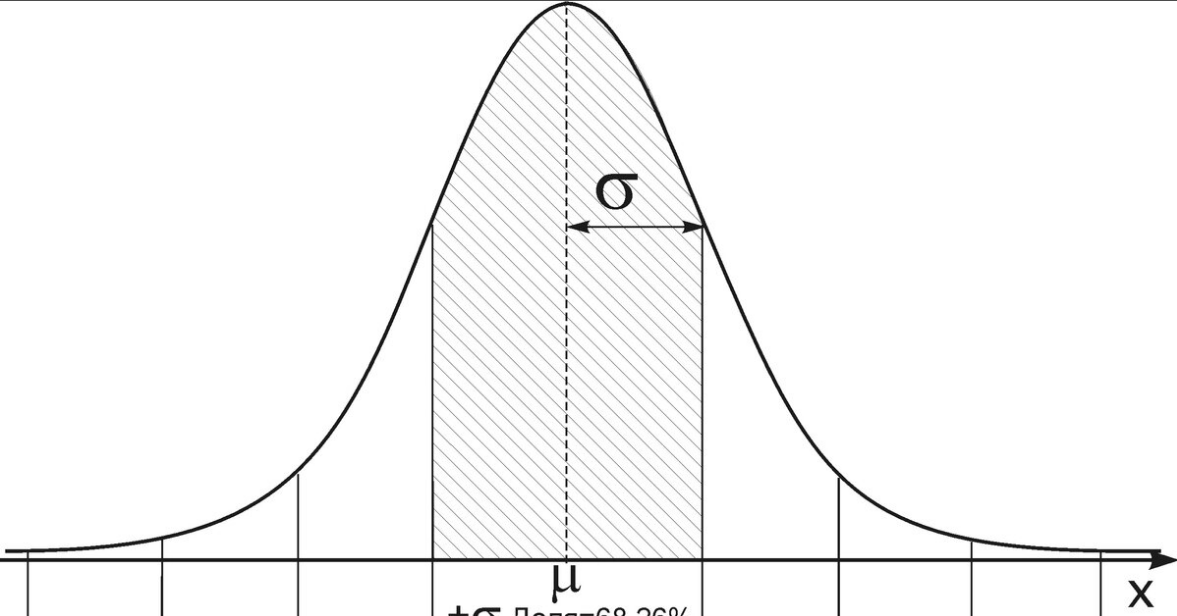 Модой M0x случайной величины называют значение этой случайной величины, наибольшее по сравнению с двумя соседними значениями, т. е. некоторый локальный максимум. 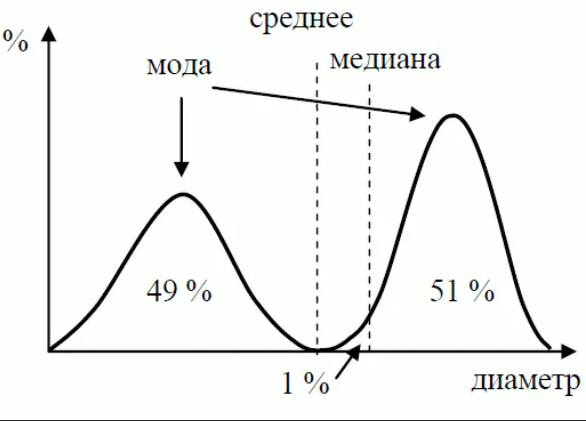 Медианой Mеx называют значение случайной величины xp , что выполняет равенство: p{x 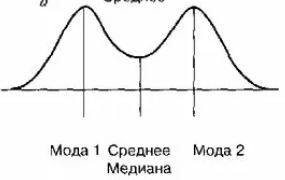 10. Законы распределения - понимание, что это такое, формулы учить необязательно (7 штук) 1. Биномиальное распределение. Дискретная случайная величина имеет биномиальный закон распределения с параметрами n и p, если она принимает значения 0, 1, 2…, k с вероятностями:  2. Распределение Пуассона. Дискретная случайная величина имеет распределение Пуассона с параметром >0, если она принимает значения 0, 1, 2…, m с вероятностями:  Распределение Пуассона часто встречается в задачах, связанных с простейшим потоком событий. Под потоком событий следует понимать последовательность событий, наступающих одно за другим в случайные моменты времени. Примерами могут служить: поток вызовов на телефонной станции, поток заявок в системе массового обслуживания, последовательность радиоактивного распада частиц. 3. Геометрическое распределение. Дискретная случайная величина имеет геометрическое распределение с параметром p, если она приминает значения 0, 1, 2…, k с вероятностями:  4. Гипергеометрическое распределение. Дискретная случайная величина имеет гипергеометрическое распределение с параметрами n, M, N, если она принимает значения 0, 1, 2…, m… min(n, M) с вероятностями: 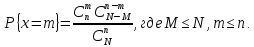 5. Нормальное распределение (Гаусса). Непрерывная случайная величина имеет нормальное распределение, если ее плотность распределения имеет вид: 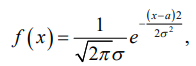 где a и некоторые постоянные, называемые параметрами распределения. 6. Равномерное распределение. Непрерывная случайная величина имеет равномерное распределение на интервале [a, b], если плотность её вероятности на этом отрезке постоянна и имеет вид: 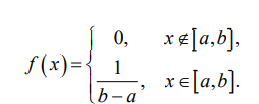 7. Показательное (экспоненциальное) распределение. Непрерывная случайная величина имеет показательное распределение с параметром >0, если плотность её вероятности имеет вид: 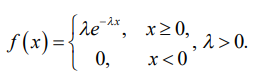 |