Высшая математика контрольная работа. математика 3 сем. 1. Определить тип и решить дифференциальное уравнение
 Скачать 250.12 Kb. Скачать 250.12 Kb.
|
|
Минобрнауки России Федеральное Государственное бюджетное образовательное учреждение высшего образования Тульский государственный университет Интернет-Институт Контрольная работа 3 семестр по дисциплине «Математика» Вариант № 1 Выполнил: Иванцов Владимир Проверила: Соколова Марина Юрьевна Тула 2018 1. Определить тип и решить дифференциальное уравнение: 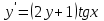 . .Решение Имеем дифференциальное уравнение с разделяющимися переменными. 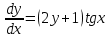 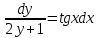 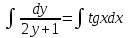 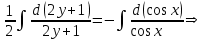 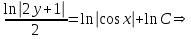 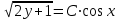 , , C – некоторая постоянная. 2. Определить тип и решить дифференциальное уравнение: 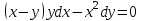 . .Решение Имеем: 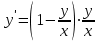 . .Имеем однородное линейное дифференциальное уравнение Замена: 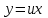 , тогда , тогда 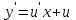 , где , где 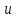 - некоторая функция от - некоторая функция от 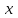 . Сделаем подстановку: . Сделаем подстановку: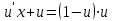 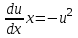 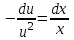 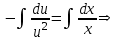 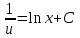 , С – некоторая постоянная. , С – некоторая постоянная.Сделаем обратную подстановку: 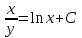 или или 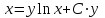 . .3. Определить тип и решить дифференциальное уравнение: 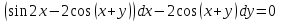 . .Решение Имеем 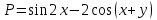 и и 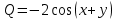 . Так как . Так как 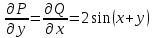 , то имеем уравнение в полных дифференциалах. , то имеем уравнение в полных дифференциалах.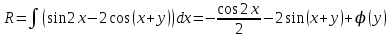 Дифференцируем 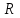 по по 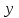 и приравниваем к и приравниваем к 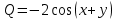 . .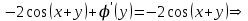 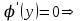 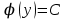 . .Следовательно, решение имеет вид 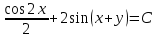 . .4. Найти решение задачи Коши: 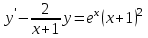 , , 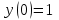 . .Решение Замена: 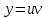 , тогда , тогда 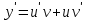 , где , где 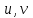 - некоторые функции от - некоторые функции от 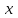 . Сделаем подстановку: . Сделаем подстановку: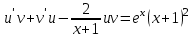 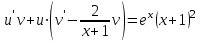 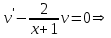 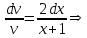 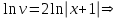 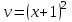 . .Найдем 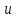 : :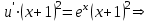 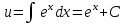 . .Тогда функция 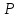 будет равна: будет равна: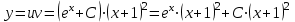 , С – некоторая постоянная. , С – некоторая постоянная.Используем начальные условия и найдем С. 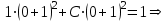 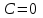 . .Окончательно, имеем решение 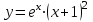 . .5. Найти решение задачи Коши: 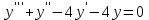 , , 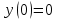 , , 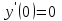 , , 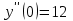 . .Решение Составим и решим характеристическое уравнение:   и и  . .Однородное решение (в данном случае и общее решение) имеет вид  , ,  - некоторые постоянные. - некоторые постоянные.Используем начальные условия и найдем  . .      . .Окончательно, имеем: 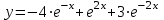 . .6. Запишите вид частного решения уравнения: 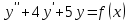 , если , если1) 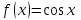 ; 2) ; 2) 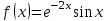 ; 3) ; 3)  ; 4) ; 4)  ; 5) ; 5)  ; ;Решение Составим и решим характеристическое уравнение:   . .Однородное решение имеет вид  , ,  - некоторые постоянные. - некоторые постоянные.1)  ; ; Частное решение будем искать в виде: 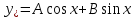 . .2) 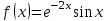 ; ; Частное решение будем искать в виде: 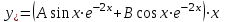 . .3) 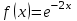 ; ; Частное решение будем искать в виде: 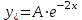 . .4) 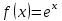 ; ; Частное решение будем искать в виде: 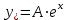 . .5) 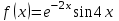 ; ;Частное решение будем искать в виде:  . .7. Найти общее решение уравнения:  . .Решение Составим и решим характеристическое уравнение:   и и 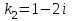 . .Однородное решение имеет вид 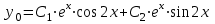 , , 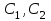 - некоторые постоянные. - некоторые постоянные.Частное решение будем искать в виде: 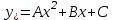 . Тогда . Тогда  и и  . . Подставим полученные производные:   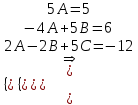 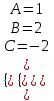 . .Тогда частное решение имеет вид 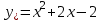 , следовательно, общее решение имеет вид , следовательно, общее решение имеет вид 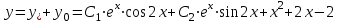 . .8. Решить систему уравнений:  . .Решение Продифференцируем второе уравнение системы:  Вместо  подставим первое уравнение системы: подставим первое уравнение системы: 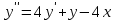 (*) (*)Из второго уравнения системы выразим 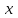 и подставим в выражение (*): и подставим в выражение (*):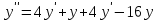 или или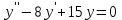 Составим и решим характеристическое уравнение:   и и  . .Однородное решение (в данном случае и общее) имеет вид  , ,  - некоторые постоянные. - некоторые постоянные.Найдем  , для этого подставим , для этого подставим  во второе уравнение системы: во второе уравнение системы: , следовательно , следовательно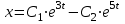 . .Ответ: 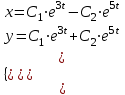 , , 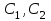 - некоторые постоянные. - некоторые постоянные.9. Исследовать на сходимость ряд 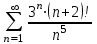 . .Решение Применим признак сходимости Даламбера:  . .Так как  , то согласно принципа сходимости Даламбера, заданный ряд расходится. , то согласно принципа сходимости Даламбера, заданный ряд расходится.10. Исследовать на сходимость ряд  . .Решение Применим радикальный признак сходимости Коши:  Так как 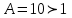 , то согласно радикального принципа сходимости Коши, заданный ряд расходится. , то согласно радикального принципа сходимости Коши, заданный ряд расходится.11. Исследовать на абсолютную и условную сходимость знакочередующийся ряд 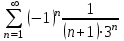 . .Решение Проверим выполнение признака сходимости Лейбница. 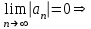 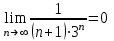 - выполняется. - выполняется. - выполняется. - выполняется.Что бы установить абсолютную или условную сходимость, исследуем знакопостоянный ряд  . .Применим признак сходимости Даламбера:  . .Так как  , то согласно принципа сходимости Даламбера, ряд , то согласно принципа сходимости Даламбера, ряд 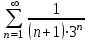 сходится. сходится.Следовательно, заданный ряд 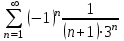 сходится абсолютно. сходится абсолютно.12. Найти область сходимости ряда 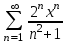 . .Решение Применим признак сходимости Даламбера: 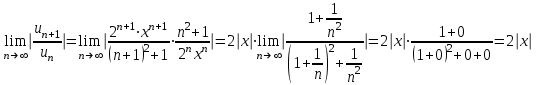 . .  . .Исследуем крайние точки. При  имеем ряд имеем ряд  . По признаку Лейбница, ряд сходится абсолютно, так как . По признаку Лейбница, ряд сходится абсолютно, так как 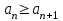 для всех для всех 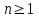 и и 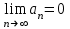 , а ряд , а ряд 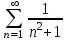 сходится по предельному признаку сходимости (сравниваем со сходящимся рядом сходится по предельному признаку сходимости (сравниваем со сходящимся рядом  ). ).При  имеем ряд имеем ряд  , который сходится по предельному признаку сходимости (сравниваем со сходящимся рядом , который сходится по предельному признаку сходимости (сравниваем со сходящимся рядом  ). ).Следовательно, область сходимости заданного функционального ряда равна  . .13. Разложить в ряд по степеням  функцию функцию  . .Решение Воспользуемся табличным разложением:  , ,  . .Получим:  Ответ:  . .14. Разложить в ряд Фурье функцию, заданную на полупериоде  графиком, приведенном на рисунке, если даны значения графиком, приведенном на рисунке, если даны значения  , ,  , ,  , ,  , и функция нечетная. Построить графики первых трех гармонических приближений функции. , и функция нечетная. Построить графики первых трех гармонических приближений функции. Решение Согласно приведенным данным, имеем следующий график:  Запишем аналитическое выражение для функции заданной графически.  Для того чтобы разложить заданную функцию в ряд Фурье по синусам, необходимо доопределить ее на полуинтервале  как нечетную. Таким образом, коэффициенты как нечетную. Таким образом, коэффициенты  и и  равны нулю. Вычислим коэффициент равны нулю. Вычислим коэффициент  . .Период равен  , полупериод , полупериод 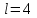 . .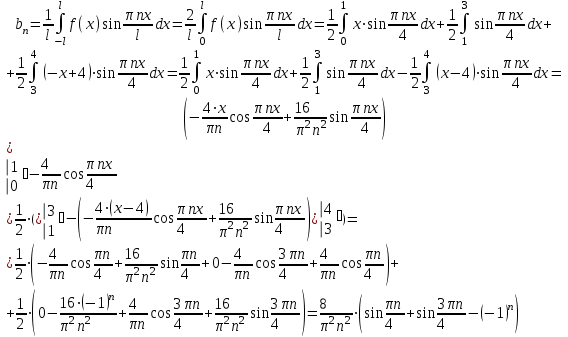 В итоге имеем: 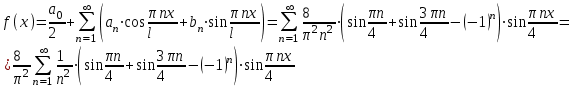 Полагая последовательно 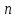 равным 1, затем 2 и 3, находим равным 1, затем 2 и 3, находим , ,  , ,  . . , , 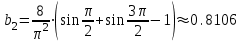 , , 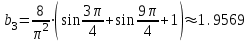 . .Амплитудный спектр будет 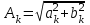 : :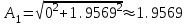 ; ;  , ,  . .Строим амплитудный спектр:  |
