С2, координатный метод. 1. Определитель второго порядка
 Скачать 188.26 Kb. Скачать 188.26 Kb.
|
|
С2 1. Определитель второго порядка 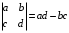 . .2. Определитель третьего порядка 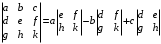 . Каждый из полученных определителей второго порядка вычисляется по формуле 1. . Каждый из полученных определителей второго порядка вычисляется по формуле 1.3. Координаты вектора Если 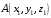 и и 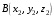 , то , то 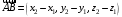 . .4. Длина вектора Если 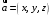 , то , то 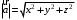 . .5. Скалярное произведение векторов Если 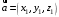 , , 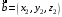 , то , то 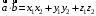 . .6. Векторное произведение векторов Если 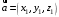 , , 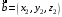 , то , то 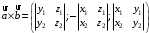 . .7. Смешанное произведение векторов Если 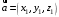 , , 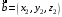 , , 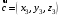 , то , то 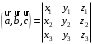 . .8. Координаты вершин правильного треугольника 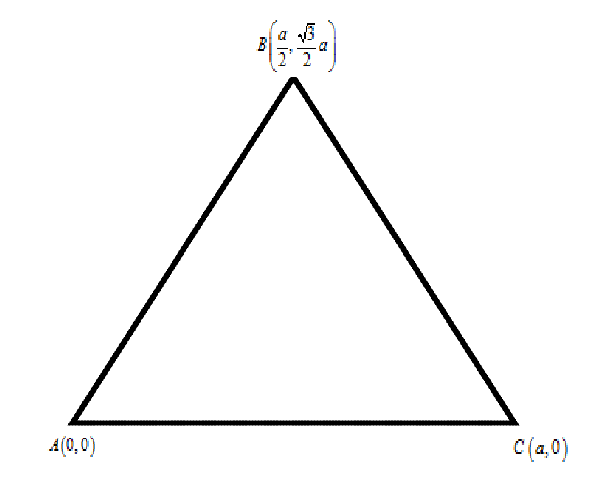 9. Координаты вершин правильного шестиугольника 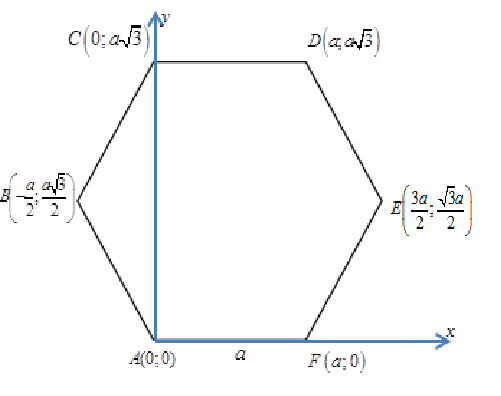 10. Координаты вершины правильной треугольной пирамиды 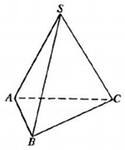 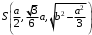 , где , где  - длина стороны основания, - длина стороны основания, 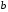 - длина боковой стороны. - длина боковой стороны.11. Координаты вершины правильной четырехугольной пирамиды 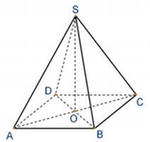 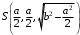 , где , где  - длина стороны основания, - длина стороны основания, 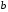 - длина боковой стороны. - длина боковой стороны.12. Координаты вершины правильной шестиугольной пирамиды 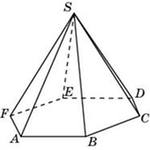 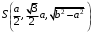 , где , где  - длина стороны основания, - длина стороны основания, 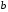 - длина боковой стороны. - длина боковой стороны.13. Уравнение плоскости Если 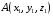 , , 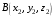 , , 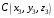 , то уравнение плоскости , то уравнение плоскости 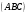 : :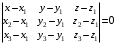 . Уравнение приводится к виду . Уравнение приводится к виду 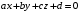 , где вектор , где вектор 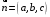 называется вектором нормали (он перпендикулярен плоскости). называется вектором нормали (он перпендикулярен плоскости).14. Расстояние от точки 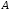 до точки до точки 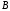 . .1) Пишем координаты точек (формулы 8-12). 2) Находим координаты вектора 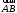 (формула 3). (формула 3).3) Находим длину вектора 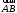 (формула 4). (формула 4).15. Расстояние от точки 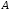 до прямой до прямой 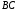 1) Пишем координаты точек (формулы 8-12). 2) Находим координаты векторов 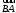 и и 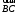 (формула 3). (формула 3).3) Находим векторное произведение 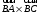 (формула 6). (формула 6).4) Находим длину векторного произведения 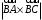 (формула 4). (формула 4).5) Находим длину вектора 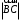 (формула 4). (формула 4).6) Искомое расстояние 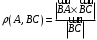 . .16. Расстояние от точки 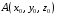 до плоскости до плоскости 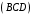 1) Пишем координаты точек (формулы 8-12). 2) Пишем уравнение плоскости 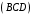 (формула 13). Приводим уравнение к виду (формула 13). Приводим уравнение к виду 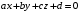 . .3) Искомое расстояние 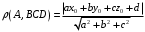 . .17. Расстояние между прямыми 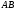 и и 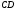 1) Пишем координаты точек (формулы 8-12). 2) Находим координаты векторов 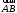 , , 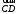 и и 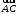 (формула 3). (формула 3).3) Находим векторное произведение 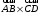 (формула 6). (формула 6).4) Находим длину векторного произведения 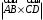 (формула 4). (формула 4).5) Находим смешанное произведение 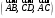 (формула 7). (формула 7).6) Искомое расстояние 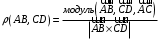 . .18. Угол между прямыми 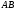 и и 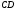 1) Пишем координаты точек (формулы 8-12). 2) Находим координаты векторов 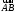 и и 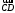 (формула 3). (формула 3).3) Находим скалярное произведение векторов 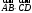 (формула 5). (формула 5).4) Находим длины векторов 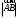 и и 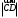 (формула 4). (формула 4).5) 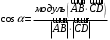 . .19. Угол между прямой 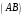 и плоскостью и плоскостью 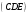 1) Пишем координаты точек (формулы 8-12). 2) Находим координаты вектора 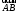 (формула 3). (формула 3).3) Находим уравнение плоскости 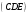 (формула 13). Получаем вектор (формула 13). Получаем вектор 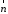 . .4) Находим скалярное произведение векторов 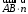 (формула 5). (формула 5).5) Находим длины векторов 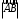 и и 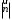 (формула 4). (формула 4).6) 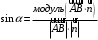 . .20. Угол между плоскостями 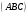 и и 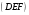 1) Пишем координаты точек (формулы 8-12). 2) Находим уравнение плоскости 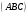 (формула 13). Получаем вектор (формула 13). Получаем вектор 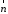 . .3) Находим уравнение плоскости 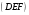 (формула 13). Получаем вектор (формула 13). Получаем вектор 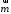 . .4) Находим скалярное произведение векторов  (формула 5). (формула 5).5) Находим длины векторов  и и  (формула 4). (формула 4).6) 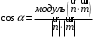 . . |
