ТФКП. 1. Построить данные числа, найти их аргументы и модули, записать в тригонометрической форме
 Скачать 84.03 Kb. Скачать 84.03 Kb.
|
|
1. Построить данные числа, найти их аргументы и модули, записать в тригонометрической форме: 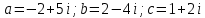 1. a = 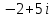 Изобразим на плоскости число: 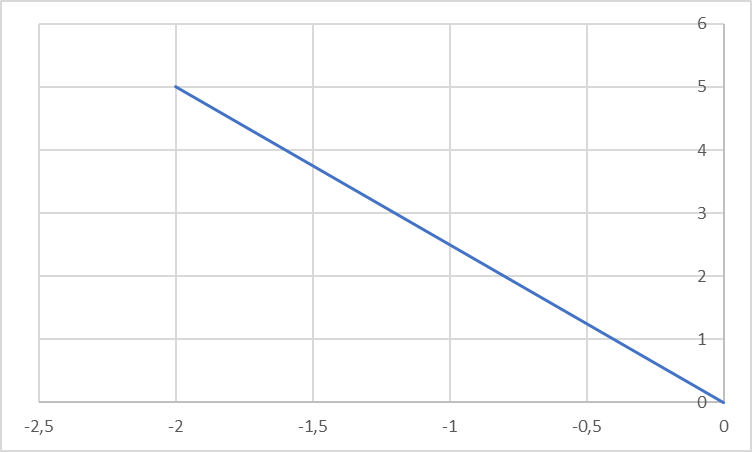 Вычислим модуль числа а: 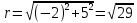 Аргумент числа а: 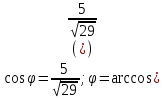 Тригонометрическая форма: 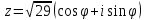 , где , где 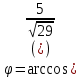 2. 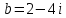 Изобразим на плоскости число:  Вычислим модуль числа а: 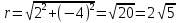 Аргумент числа а: 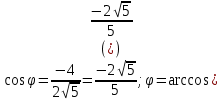 Тригонометрическая форма: 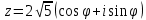 , где , где 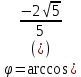 3. 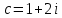 Изобразим на плоскости число: 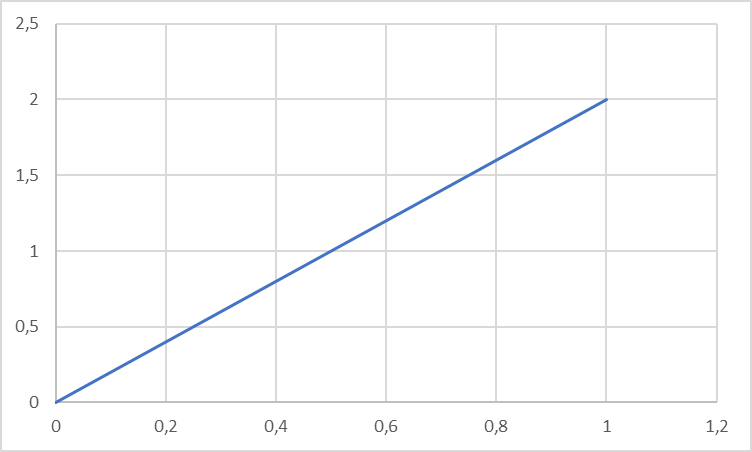 Вычислим модуль числа а:  Аргумент числа а: 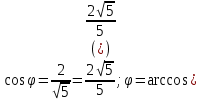 Тригонометрическая форма: 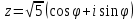 , где , где 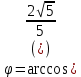 2. Вычислить, используя формулы Моавра. Показать на тригонометрическом круге особенность расположения корней: 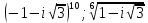 1. Комплексное число  находится в 3 четверти, поэтому: находится в 3 четверти, поэтому: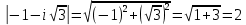  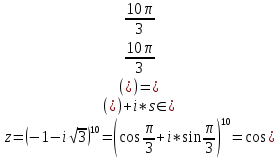 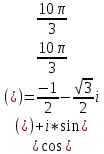 2. Комплексное число 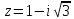 находится в 4 четверти, поэтому: находится в 4 четверти, поэтому: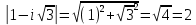 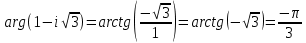 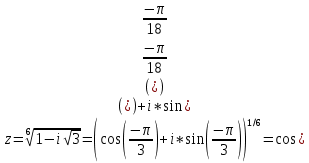 3. Изобразить на плоскости множество точек z, удовлетворяющих условию: 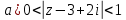 Преобразуем выражение:  Тогда: 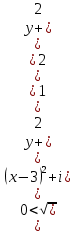 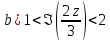 Так как 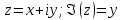 Преобразуем выражение: 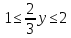 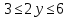 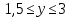 4. Найти предел последовательности или доказать ее расходимость: 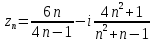 По условию: 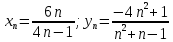 Найдем пределы последовательностей действительных чисел: 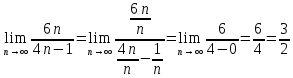 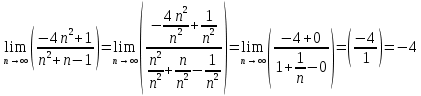 То есть а = 1,5; 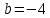 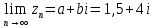 Ряд сходится. 5. Исследовать ряд на сходимость и абсолютную сходимость: 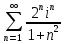 Составим ряд из модулей членов данного ряда: 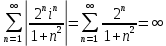 Значит, ряд не сходится. 6. Найти радиус и круг сходимости степенного ряда, изобразить круг сходимости: 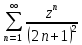 Применим признак Коши: 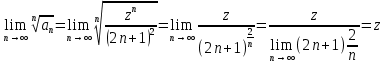 При 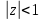 ряд сходится, а при ряд сходится, а при 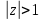 расходится. расходится.Следовательно, 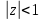 является кругом сходимости с центром в точке z0 = 0 и радиуса 1 является кругом сходимости с центром в точке z0 = 0 и радиуса 1Изобразим круг сходимости: 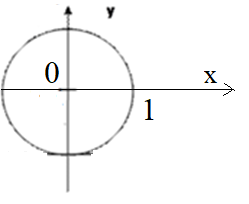 7. Выделить действительную и мнимую части данной функции. Найти образы точек z1= -i, z2 = 1 – i, z3 = 1 при отображении заданной функции. Исследовать функцию на непрерывность. 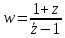 Преобразуем: 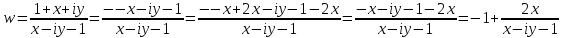 Следовательно, равенство 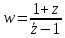 равносильно двум равенствам: равносильно двум равенствам: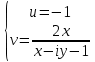 Функция имеет разрыв в точке (1; 0). Найдем образы точек: 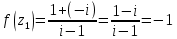 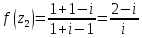 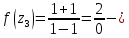 не существует, z = 1 – точка разрыва не существует, z = 1 – точка разрыва 8. В какой угол перейдет вектор а после поворота на угол α? β? Записать функцию, осуществляющую указанное отображение.  Построим комплексное число 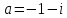 : :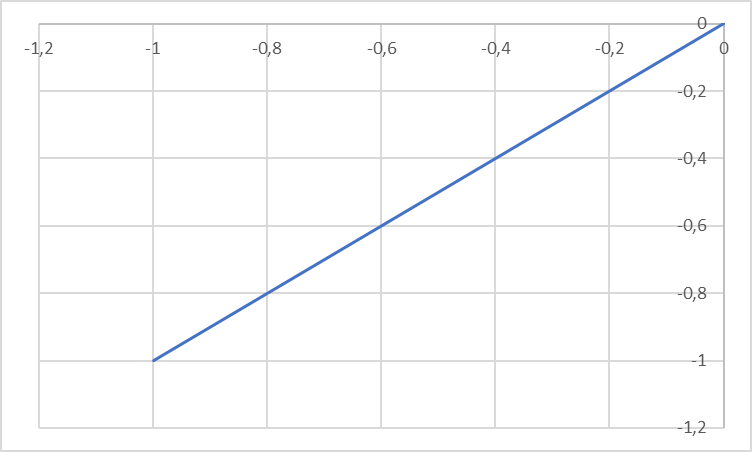 Угол поворота равен 210°. При повороте на 60° по часовой стрелке угол поворота равен 270°. При повороте на -60° угол поворота равен 150°. 9. Исследовать функцию на дифференцируемость и аналитичность: 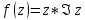 Пусть w = 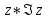 , так как z = x + iy, то , так как z = x + iy, то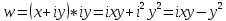 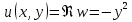 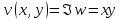 Значит, 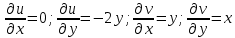 Условия Коши-Римана: 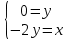 Значит, функция дифференцируема и аналитична на всей числовой прямой. 10. Восстановить аналитическую функцию w = u + iv по ее действительной или мнимой части. Вычислить производную полученной функции. a) 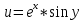 Функция аналитическая, поэтому дифференцируема в каждой точке области аналитичности; т.е. выполняются условия Коши-Римана:  По известной действительной части находим: 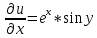  Тогда: 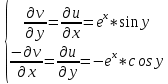 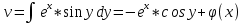 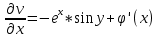 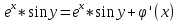 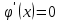 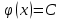 Значит:  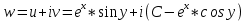 b) 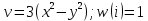 Функция аналитическая, поэтому дифференцируема в каждой точке области аналитичности; т.е. выполняются условия Коши-Римана:  По известной мнимой части находим: 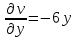 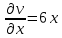 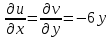 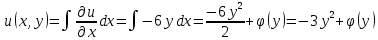 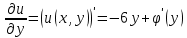 По условиям Коши-Римана: 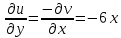 Поэтому 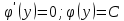 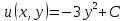 Значит: 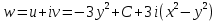 11. Вычислить следующие интегралы: 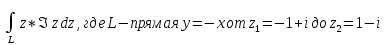 По определению: 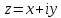 Перепишем подынтегральную функцию в виде:  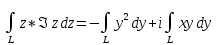 Так как y = 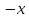 , значит, dy = -dx: , значит, dy = -dx: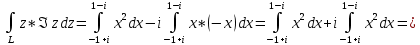 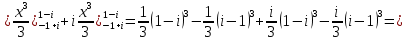 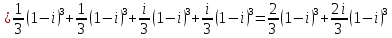 12. Вычислить следующие интегралы: а) 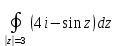 Функция аналитическая всюду в 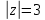 : :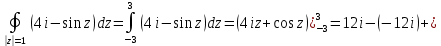 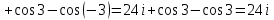 b)  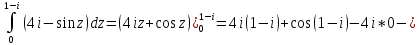 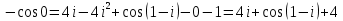 13. Вычислить, используя интегральную формулу Коши: 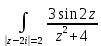 Знаменатель обращается в ноль при z1 = 2i; z2 = -2i. В круге 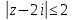 лежит одна точка, в которой знаменатель обращается в 0: z1 = 2i. лежит одна точка, в которой знаменатель обращается в 0: z1 = 2i. 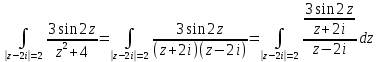 Функция 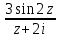 является аналитической в круге является аналитической в круге 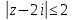 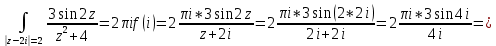 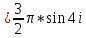 14. Вычислить, найти модуль и аргумент: 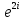 Воспользуемся формулой Эйлера: 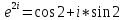 Так как 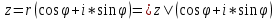 , , то модуль комплексного числа |z| = 1 15. Вычислить Ln и ln следующих чисел: 4i / 5; 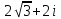 ; ; 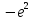 1. z = 4i/5 |z| = 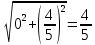 arg (z) = 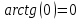 Тогда: ln z = ln 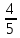 + 0i = ln + 0i = ln 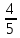 2. z = 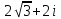 |z| = 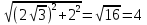 arg (z) = 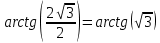 Тогда: ln z = ln 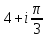 Ln z = ln 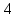 + i + i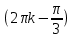 3. z = 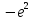 |z| =  arg (z) = 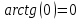 Тогда: ln z = ln 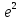 + 0i = 2 + 0i = 216. Вычислить, найти модуль: sin(1+4i); cos(-2i) 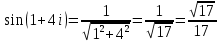 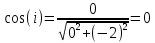 |
