1. Предельный момент для сечения при изгибе
 Скачать 32.83 Mb.
|
                    1.Предельный момент для сечения при изгибеПусть материал по-разному работает на растяжение и сжатие, и  -предел текучести при растяжении, а  - предел текучести при сжатии.Рассмотрим сечение, полностью перешедшее в пластическое состояние. Положение нейтральной оси (  ) в предельном состоянии найдем из равенства нулю проекций сил, действующих в сечении на ось балки:  если материал одинаково работает на растяжение и сжатие, то   и условие выглядит:  Предельный момент в сечении равен  , где  и  статические моменты растянутой и сжатой зоны сеченияотносительно оси  .Если материал одинаково работает на растяжение и сжатие, то   Величину  называется пластическим моментом сопротивления.Если ось  - ось симметрии, то нейтральная ось совпадает с ней и  где  - статический момент половины сечения относительно нейтральной оси. 2. Расчет балок по методу предельных нагрузок Состояние балки станет предельным в том случае, когда в ней появится столько пластических шарниров, что система станет кинематически изменяемой. Когда момент в сечении достигает предельного значения, то сечение не способно воспринимать возрастающую нагрузку и ведет себя как шарнир, называемый пластическим шарниром. Этот шарнир характерен следующим: а) Он односторонний и при уменьшении нагрузки закрывается. б) В нем действуют две противоположно направленные пары с моментами равными  Введение пластического шарнира означает идеализацию картины распространения пластических деформаций в балке при поперечном изгибе. Пластическая зона распространяется по длине балки Нагрузка, соответствующая предельному состоянию называется предельной нагрузкой. Во многих случаях мы будем опираться на кинематический экстремальный принцип, выдвинутый в 1938 г. А.А.Гвоздевым: Истинной форме перехода в предельное состояние соответствует минимальное значение предельной нагрузки. Суть состоит в том, что мы перебираем все кинематически возможные механизмы перехода в предельное состояние, определяем для каждого из них предельную нагрузку и останавливаемся на минимальной по величине предельной нагрузке. 3.Напряжение. Понятие напряженного состояния 4.Тензор напряжений. Закон парности касательных напряжений. 4.Определение напряжений по произвольной площадке в случае, когда задан тензор напряжений.  (1) 5.Главные площадки и главные напряжения. Определение главных напряжений в общем случае 6.Инварианты напряженного состояния Инвариантами напряжённого состояния-скалярные величины, не зависящие от выбора исходных трёх взаимно перпендикулярных площадок. Они определяются следующим образом  линейный инвариант. квадратичный инвариант, равный сумме миноров элементов, стоящих на главной диагонали. кубический инвариант, равный определителю матрицы7.Определение напряжения по площадкам, параллельным направлению одного из главных напряжений. Круговая диаграмма Мора. Рассмотрим элемент в виде прямоугольного параллелепипеда, грани которого являются главными площадками (Рис.6). Рассмотрим семейство площадок, параллельных направлению главного напряжения  . Выделим из параллелепипеда плоскостью, наклонённой под углом  к вертикальной грани, треугольную призму (Рис.6). На наклонной грани призмы действуют нормальное напряжение  и касательное напряжение  . Выразим их через главные напряжения. Составим уравнения равновесия для призмы. Рис.6 Проектируя на направление нормали к площадке, получим  .Проектируя на направление  , имеем .После очевидных сокращений и перехода к функциям аргумента  получим: (1.7) Если рассматривать и  как координаты соответствующей координатной плоскости, то можно обнаружить, что (7) представляют собой параметрические уравнения окружности. На самом деле:   .Последнее соотношение представляет собой уравнение окружности, центр которой лежит на оси  и имеет координату  . Радиусом окружности  .  Полученный круг называется круговой диаграммой Мора. Если не принимать во внимание знак касательного напряжения, то можно ограничиться построением только верхней половины круга Мора.Построенная диаграмма имеет следующий смысл: каждой площадке параллельной направлению напряжения  соответствует точка на окружности.Можно построить круговые диаграммы и для площадок параллельных направлению главных напряжений  и . См. рисунок.Площадкам общего положения, не параллельным ни одному из главных напряжений, соответствуют точки расположенные в заштрихованной области.   Наложим круговые диаграммы на один чертеж 8.Определение главных напряжений в случае, когда известно положение одной из главных площадок. Пусть  главное напряжение (Рис.11). Требуется найти два другие главные напряжения. Воспользуемся круговой диаграммой Мора. Площадкам 1 и 2 соответствуют точки на координатной плоскости  . Нанесём их и проведём окружность, проходящую через эти точки, центр которой лежит на оси  . Точки пересечения окружности и оси  дадут значения главных напряжений  и  . Найдём их. Координата центра окружности равна Радиус окружности: .  Тогда    .Мы получили нам уже знакомую формулу, выведенную для случая плоского напряжённого состояния. Напряжение  не влияет на два других главных напряжения. Сопоставляя  ,  и  , устанавливаем  .9.Классификация напряженных состояний В зависимости от числа главных напряжений отличных от нуля напряжённые состояния бывают: 1.1) Трёхосные или объёмные напряжённые состояния – случай, когда ни одно из главных напряжений не равно нулю. 1.2) Напряжённое состояние называется двухосным или плоским, если только два главных напряжения отличны от нуля. В этом случае кубический инвариант  равен нулю. Характеристическое уравнение принимает вид  Одно из главных напряжений равно нулю, а два других определяются из решения приведенного выше квадратного уравнения. Если напряженное состояние задано напряжениями по площадкам, одна из которых, например, с внешней нормалью  , является той главной площадкой, по которой главное напряжение равно нулю, то тензор напряжений принимает вид Инварианты напряжённого состояния примут вид:  ,  . Подставляя это в выражение для главных напряжений, получим формулу .(1.6) 1.3) Если кубический  и квадратичный инвариант одновременно равны нулю, то лишь одно главное напряжение отлично от нуля. Оно называется одноосным или линейным и возникает, например, при растяжении и сжатии при чистом изгибе.В зависимости от знаков главных напряжений: 2.1:Трёхосные растяжения, когда ни одно из главных напряжений не является сжимающим. 2.2:Трёхосные сжатия, когда ни одно из главных напряжений не является растягивающим. 2.3:Смешанные напряжённые состояния, когда  и  имеют разные знаки.10. Тензор деформаций. Связь между компонентами тензора деформаций и компонентами вектора перемещений.  Деформированное состояние в точке определено, т.е. можно вычислить удлинение по любому направлению, проходящему через данную точку, если задан тензор деформаций. Тензор деформаций - совокупность удлинений по трём взаимно перпендикулярным направлениям и углов сдвига в плоскостях трёх площадок, нормальных к данным направлениям. Он имеет видЗдесь:  деформации относительного удлинения в направлении соответствующих осей;  деформации сдвиг в соответствующих координатных плоскостях. Тензор деформаций симметричен. Теория деформированного состояния аналогична теории напряжённого состояния. Рассмотрим малый элемент, который в процессе деформации изменил свою конфигурацию. Деформация в направлении оси   .  . ;  ;  ; ;  ;  .11. Обобщенный закон Гука Между компонентами тензора напряжений и компонентами тензора деформаций существует связь, которая может быть установлена только экспериментальным путём. Для большинства материалов при умеренных напряжениях эта связь может быть принята линейной, т.е. может быть принят закон Гука, который для одноосного состояния запишется  .Воспользуясь этим соотношением и принципом независимости действия сил, получим закон Гука для трёхосного напряженного состояния. Рассмотрим малый элемент параллелепипеда. Пусть на элемент действует только напряжение  , а  , тогда деформации в направлении координатных осей будут равны ;  .При  ,  :  ;  .При  ,  : ;  .Деформация удлинения в направлении оси  при совместном действии всех напряжений будет равна .Аналогичным образом определятся деформации в направлении других координатных осей. Подставляя выражения для  , после очевидных преобразований получим три уравнения , , .Добавим к этим уравнениям ещё три соотношения, вытекающие из закона Гука при чистом сдвиге  ;  ;  .Три упругие постоянные: модуль упругости  , модуль сдвига  и коэффициент Пуассона  не являются независимыми. Они связаны между собой соотношением .Шесть полученных уравнений, связывающих между собой компоненты тензоров напряжений и деформации, составляют так называемый обобщённый закон Гука. 12. Понятие о предельном напряженном состоянии (критерии пластичности и разрушения). Эквивалентное напряжение. Напряженное состояние, при котором происходит коренное изменение механического состояния материала в точке, называется предельным напряженным состоянием. Два вида предельных напряженных состояний: 1) Переход материала в данной точке в пластическое состояние. 2) Наступление стадии разрушения.  Где:  - коэффициент запаса по текучести,  - предел текучести при растяжен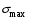ии,  - напряжение в наиболее опасной точке конструкции.Под коэффициентом запаса будем понимать число, в которое надо увеличить одновременно все компоненты напряженного состояния чтобы оно стало предельным. Различные напряженные состояния, имеющие одинаковые коэффициенты запаса, т.е. одинаково близкие к предельному напряженному состоянию, будем называть равноопасными. Эквивалентное напряжение – напряжение, которое надо создать в растянутом образце, чтобы его напряженное состояние было равноопасно заданному сложному напряженному состоянию. Величина эквивалентного напряжения устанавливается с помощью соответствующей теории (гипотезы) предельного напряженного состояния. Величина коэффициента запаса по текучести определяется через эквивалентное напряжение следующим образом:   13. Теория наибольших касательных напряжений (Треска – Сен-Венана). Согласно этой теории считается, что критерием перехода в пластическое состояние является величина наибольшего касательного напряжения. Так как оба состояния равноопасны, а критерием перехода в предельное состояние является величина наибольшего касательного напряжения, то естественно считать, что наибольшие касательные напряжения в обоих случаях можно считать равными   23. Критерий Гриффитса. 18. Расчет цилиндрических и сферических оболочек, находящихся под действием внутреннего давления. |