1. Расчет линейной электрической цепи постоянного тока
 Скачать 246.55 Kb. Скачать 246.55 Kb.
|
|
Изм. Лист № документа Подпись Дата Лист КР.2015.2-360331.11С.30 1.Расчет линейной электрической цепи постоянного тока.Рассчитать токи в ветвях электрической цепи используя метод преобразования электрической цепи при определении  приведённой схемы промежуточного преобразования. приведённой схемы промежуточного преобразования.Вычислить мощность источника и суммарную мощность приемника. Составить баланс мощностей. Числовые параметры схемы эл. Цепи постоянного тока
Схема электрической цепи  Решение 1.1.1.Определяем направление тока в цепи 1.1.2.Находим сопротивление R45 где R4 и R5 соединены параллельно. Схема приобретает следующий вид:  R45=R4+R5=150+400=550Ом R45=R4+R5=150+400=550Ом1.1.3. Находим сопротивление R23, где R2иR3соединены последовательно. Схема преобразуется в следующий вид:  R23=R2+R3=140+60=200Ом R23=R2+R3=140+60=200Ом1.1.4.Находим сопротивление R456,где R45иR6соединены параллельно. Схема приобретает следующий вид: 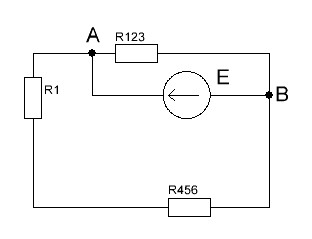  1.1.5 Находим сопротивления R123,где R1 и R23 соединены последовательно. Схема преобразует следующий вид: R123=R1+R23= 5+200=84,6Ом 1.1.6Находим сопротивление Rэкв, которое представляет собой параллельное соединение R123иR456, При этом схема имеет следующий вид: 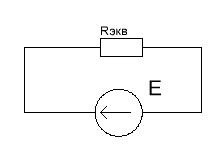  1.1.7. Находим ток всей цепи по закону Ома 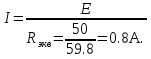 1.1.8.Находим напряжение на участках UАВ 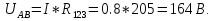 1.1.9. Находим ток на втором и третьем участке цепи  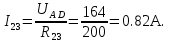 1.1.10. Находим напряжение на участке CD. 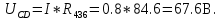 1.1.11.Находим ток на 4и5 участке цепи   Находим тока на 1и6участке цепи 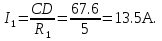  1.2.1.Определяем мощность источника  1.2.2.Находим мощность на каждом электро приёмнике   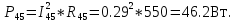  1.2.3. Определяем суммарную мощность эл. приёмников цепи. ��P=P1+P23+P45+P6=911.2+134.4+40.2+44.8=1136.6ВT. 1.2.4.Составляем баланс мощностей. Сравниваем мощность источника и суммарную мощность приёмников. В процентном соотношении погрешность ∆ 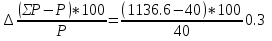 2.Анализ электрического состояния линейной электрической цепи постоянного тока. Расчет линейных электрических цепей постоянного тока.Для электрической цепи заданного варианта выполнить следующее: 2.1.Определить токи во всех ветвях схемы, используя метод узлового и контурного уравнения. 2.2.Определить токи во всех ветвях схемы, используя метод контурных токов. 2.3.Определить токи во всех ветвях схемы, используя метод наложения. Составить баланс мощностей для заданной схемы. Результаты расчетов по пунктам 2.1.-2.3. представить в виде таблицы. 2.4.Определить токи в одной из ветвей, используя метод эквивалентного генератора напряжения. 2.5.Построить потенциальную диаграмму для любого замкнутого контура включающего ЭДС 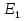 и и 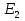 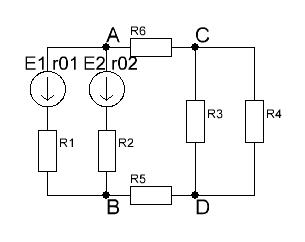
2.1.1.Определить токи во всех ветвях схемы, используя метод узлового и контурного уравнения.2.1.2 Составляем систему уравнений для трёх узлов А.В.С, для контура с ЭДС и для контура без ЭДС. Для узлов уравнений составляем по первому закону Кирхгофа, для контуров по второму закону Кирхгофа.  2.2.2Расчёт эл. цепи методом контурных токов. Суть метода состоит в том, что в ветви протекает один контурный ток, то действительный ток будет равен этому контурному току. Если же больше одного то действительный ток равен алгебраичной сумме контурных токов, протекающих в этой ветви.    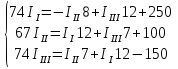 Далее  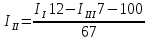    Находим значение токов с помощью матрицы 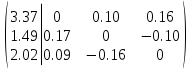 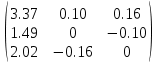 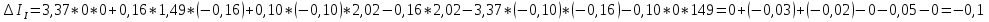 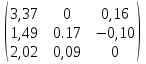 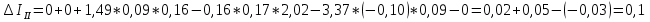 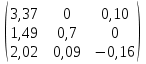 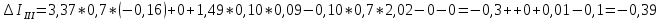 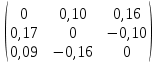  2.2.3. Определяем токи 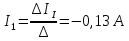 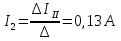 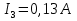 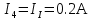 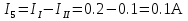  2.3.1. Определяем направление токов  2.3.2.Приобазовываем схему и вычисляем сопротивление  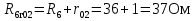 2.3.3.Преобразовываем схему и рассчитываем неизвестное сопротивление  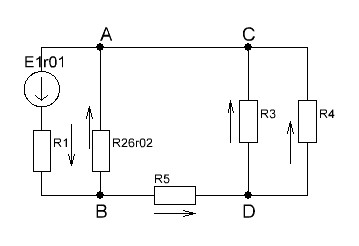  2.3.4.Преобразовываем схему и рассчитываем сопротивление 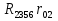 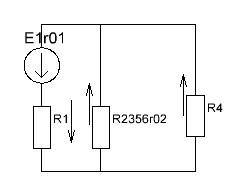 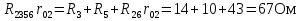 2.3.5.Преобразовываем схему и рассчитываем сопротивление  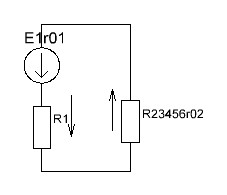 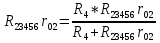 = = 2.3.6. Преобразовываем схему и рассчитываем сопротивление   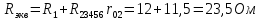 2.3.7.Находим токи от второго ЭДС 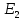  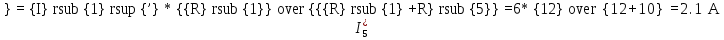    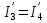 2.3.8.Преобразовываем схему и находим сопротивление цепи ЭДС Е1   2.3.9.Находим сопротивление  и схема приобретает следующий вид и схема приобретает следующий вид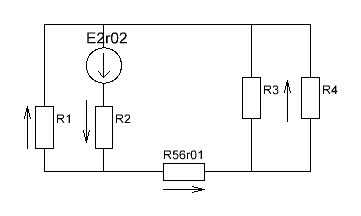 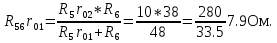 2.3.10. Находим сопротивление 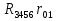 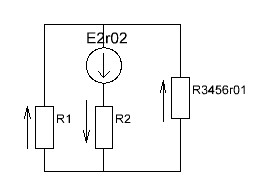  2.3.11. Находим сопротивление 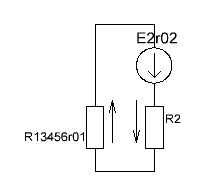  2.3.12. Находим  , схема имеет такой вид , схема имеет такой вид   2.3.13.Находим токи от первого ЭДС     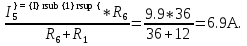  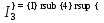 2.3.14.Находим токи во всех участках цепи 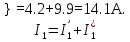   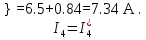 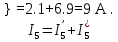 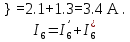 Составим таблицу результатов вычислений по пунктам 2.1.-2.3.
2.4. Определить ток в ветви с с сопротивлением эквивалентного генератора  2.4.1. Определить направление тока холостого хода в цепи и I1 2.4.2. Произвести разрыв цепи вместо R1(а,в) 2.4.3. Определить ток холостого хода цепи  2.4.4. Определяем пошагово сопротивление 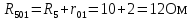    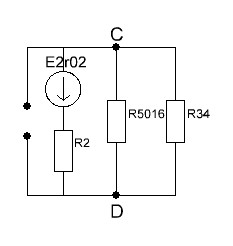 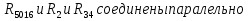  Находим  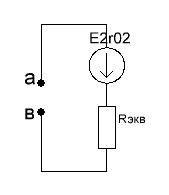 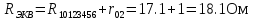 2.4.5. Определить потенциалы в точках а и в 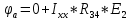  2.4.6. Определить напряжение 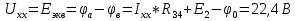 2.4.7. Определить ток в ветви сопротивления R2  2.5. Построим потенциальною диаграмму диаграмму 2.5.1.Чертим схему в которой выбираем защитный контур с ЭДС Е2. 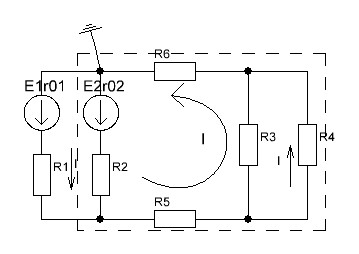 2.5.2.Определяем направление токов 2.5.3. Находим потенциалыв точках Принимаем ��0=0  Потенциалы в точкеВ��в=0 Потенциалы в точке  Потенциалы в точке 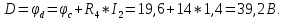  2.5.4.Строим диаграмму замкнутого контура с ЭДС 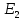 |

 , A
, A , A
, A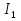 , A
, A , A
, A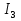 , A
, A , A
, A , A
, A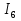 A
A