1. расчет статически определимого стержня
 Скачать 279.74 Kb. Скачать 279.74 Kb.
|
|
1. РАСЧЕТ СТАТИЧЕСКИ ОПРЕДЕЛИМОГО СТЕРЖНЯ 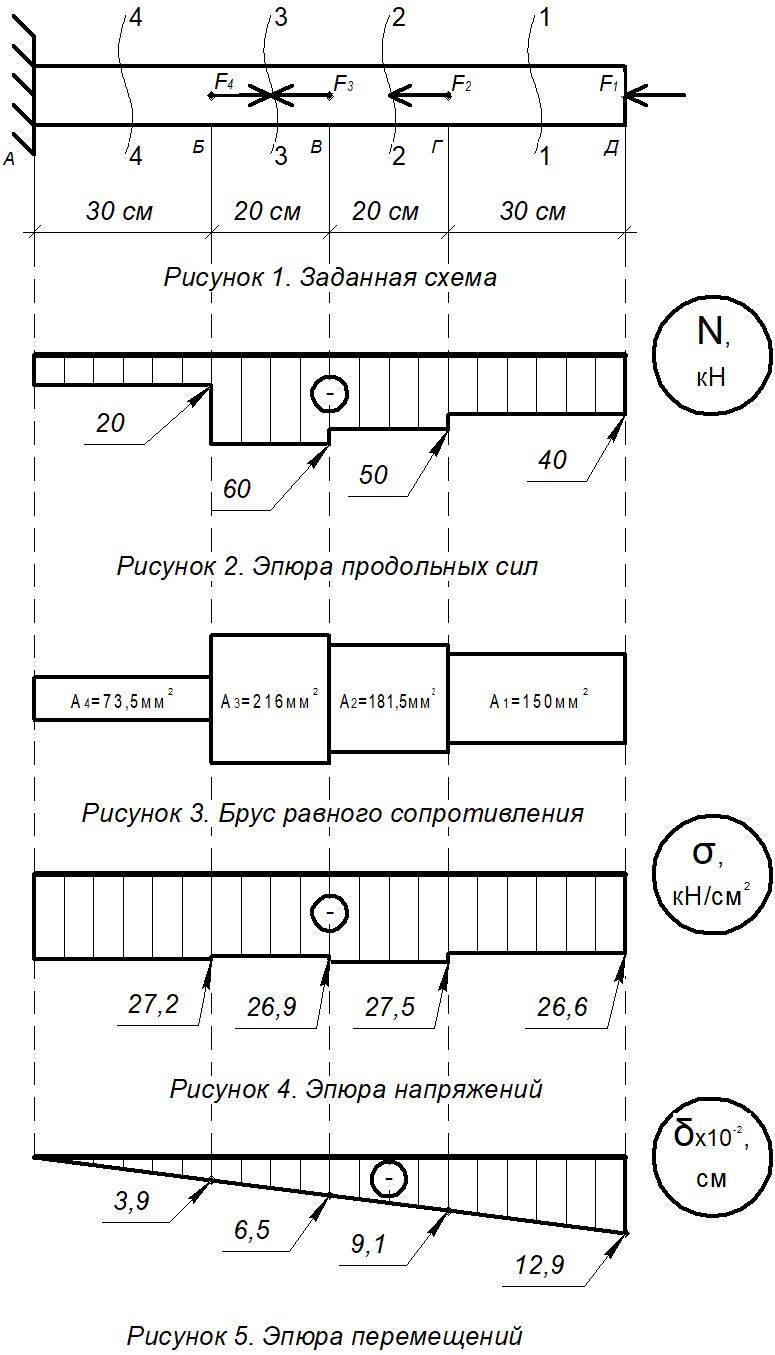 Исходные данные: Из табл. 3.1 принимаем исходные данные 6-ого варианта.  Для Ст35: Е=2.1*104 кН/см2, [Ơp]=18 кН/см2, [Ơсм]=27 кН/см2 Решение: 1) Разбиваем стержень по длине на участки, начиная от заделки. Вычисляем продольные усилия N по методу сечений: разбиваем стержень на сечения по участкам, составляем уравнение суммы всех на ось Z и вычисляем продольные усилия: ∑F(z)=0; Сечение 1-1: N1=-F1=-40 кН (смятие); Сечение 2-2: N2=-F1-F2=-50 кН (смятие); Сечение 3-3: N3=-F1-F2-F3=-60 кН (смятие); Сечение 4-4: N4=-F1-F2-F3+F4=-20 кН (смятие); Строим эпюру продольных сил. 2) Проектный расчет. На основании условия прочности раст/сж Ơi=  ≤ [Ơ], определяем поперечные сечения участков (прямоугольник) Ai=Ni/[Ơ], т.к. А=b*h=b*1.5b=1.5b2, то сторона b прямоугольника будет равна bi= ≤ [Ơ], определяем поперечные сечения участков (прямоугольник) Ai=Ni/[Ơ], т.к. А=b*h=b*1.5b=1.5b2, то сторона b прямоугольника будет равна bi= . .Сечение 1-1: b1=  - прим. по ГОСТ 10мм - прим. по ГОСТ 10ммСечение 2-2: b2=  - прим. по ГОСТ 11мм - прим. по ГОСТ 11ммСечение 3-3: b3=  - прим. по ГОСТ 12мм - прим. по ГОСТ 12ммСечение 4-4: b4=  -прим. по ГОСТ 7 мм -прим. по ГОСТ 7 ммТогда площади Ai по ГОСТу будут равны: А1=1,5*12=1,5см2, А2=1,5*1,12=1,815см2, А3=1,5*1,22=2,16см2, А4=1,5*0,72=0,735см2; Определяем погрешность ΔАi= 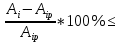 +-5% - для инженерных расчетов допускается погрешность в 5%. +-5% - для инженерных расчетов допускается погрешность в 5%.ΔА2=  +-5% (норма) +-5% (норма)ΔА2=  +-5% (норма) +-5% (норма)ΔА3=  +-5% (норма) +-5% (норма)ΔА4= 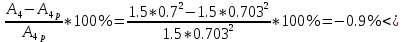 +-5% (норма) +-5% (норма)Вычерчиваем брус равного сопротивления. 3) Проверочный расчет. Расчет производим из условия прочности при раст/сж: Сечение 1-1: Ơ1=  < [Ơсм]= 27 < [Ơсм]= 27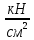 (недогрузка); (недогрузка);Сечение 2-2: Ơ2= 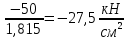 > [Ơсм]= 27 > [Ơсм]= 27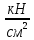 (перегрузка); (перегрузка);Сечение 3-3: Ơ3=  < [Ơсм]= 27 < [Ơсм]= 27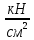 (недогрузка); (недогрузка);Сечение 4-4: Ơ4= 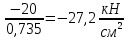 > [Ơсм]= 27 > [Ơсм]= 27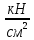 (перегрузка); (перегрузка);Определяем погрешность ΔƠi=  +-5%: +-5%:ΔƠ1=  = =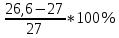 = -1,5 < +-5% (прочность обеспечена); = -1,5 < +-5% (прочность обеспечена);ΔƠ2=  = = = 1,9 < +-5% (прочность обеспечена); = 1,9 < +-5% (прочность обеспечена);ΔƠ3=  = = = -0,4 < +-5% (прочность обеспечена); = -0,4 < +-5% (прочность обеспечена);ΔƠ4=  = = = 0,8 < +-5% (прочность обеспечена); = 0,8 < +-5% (прочность обеспечена);Строим эпюру нормальных напряжений. 4) Построение эпюры продольных перемещений δ. Найдем деформации участков стержня по з-ну Гука Δli=Ơi*li/E: Участок А-Б: ΔlАБ=Ơ4*lАБ/E = -27,2*30/21000 = -0,039 см; Участок Б-В: ΔlБВ=Ơ3*lБВ/E = -26,9*20/21000 = -0,026 см; Участок В-Г: ΔlВГ=Ơ2*lВГ/E = -27,5*20/21000 = -0,026 см; Участок Г-Д: ΔlГД=Ơ1*lГД/E = -26,6*30/21000 = -0,038 см; Найдем перемещения по сечениям стержня, для этого воспользуемся формулой δi= δi-1+ Δli-ого участка. Учитывая, что в заделке перемещения δА=0, имеем: Сечение 1-1: δБ= δА+ ΔlАБ = 0 – 0,039 = -0,039 см; Сечение 2-2: δВ= δБ+ ΔlБВ = -0,039 – 0,026 = -0,065 см; Сечение 3-3: δГ= δВ+ ΔlВГ = -0,065 – 0,026 = -0,091 см; Сечение 4-4: δД= δГ+ ΔlГД = -0,091 – 0,038 = -0,129 см; По полученным результатам строим эпюру перемещений. |
