Вариант 550502-8 (E5-МЭГ4). 1. Расшифруем задание согласно исходному варианту 5505028 Определим полные комплексные сопротивления ветвей
 Скачать 0.55 Mb. Скачать 0.55 Mb.
|
|
1. Расшифруем задание согласно исходному варианту 550502-8: 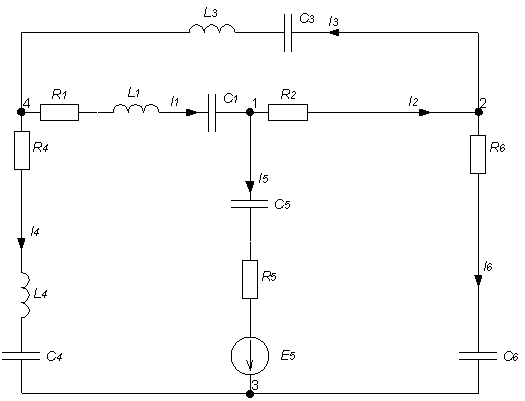 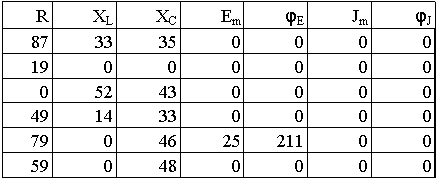 Определим полные комплексные сопротивления ветвей: 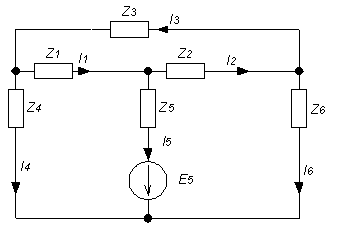 2. Рассчитаем методом эквивалентных преобразований токи во всех ветвях заданной цепи. Преобразуем треугольник Z1, Z2, Z3 в звезду: 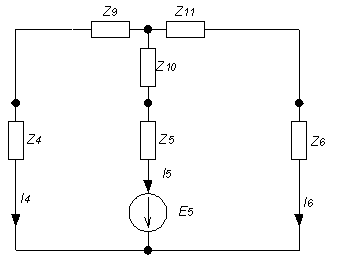 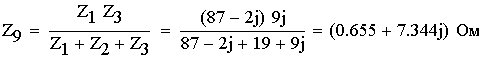 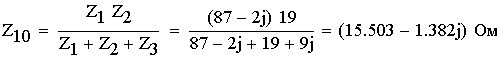 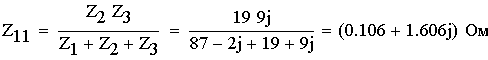 Преобразуем схему: 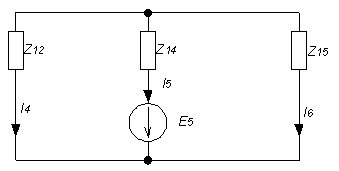 Преобразуем схему к одноконтурной: 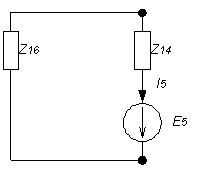 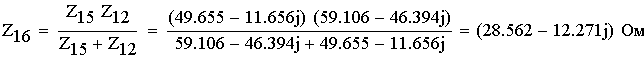 Разворачивая схему в обратном порядке определим токи во всех ветвях: 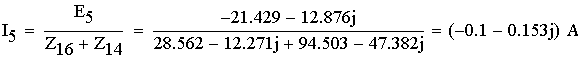 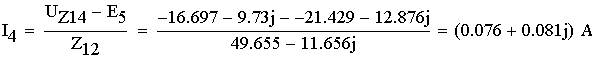 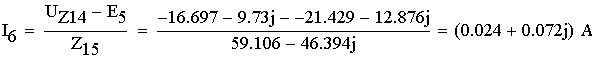 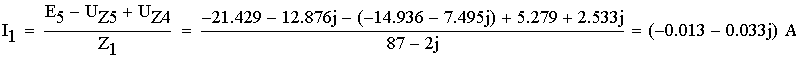 3. Составим баланс мощностей: 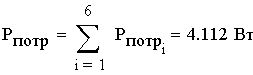 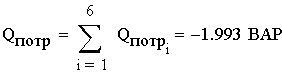 4. Определим токи в ветвях исходной схемы методом законов Кирхгофа при помощи решения СЛАУ в программе MatCAD14. 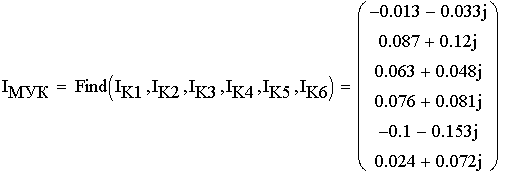 Сравним данные, рассчитанные ранее и полученные путем решения в MathCAD - как видно они практически идентичны: 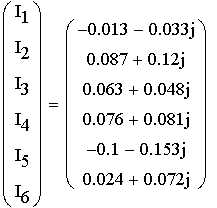 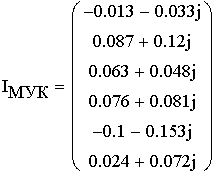 5. Определим токи в ветвях исходной схемы методом контурных токов при помощи решения СЛАУ в программе MatCAD14. 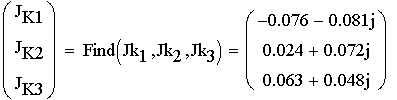 Определим токи в ветвях схемы через рассчитанные значения контурных токов: 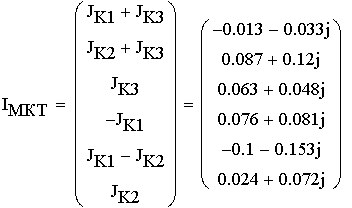 Сравним данные, рассчитанные ранее и полученные путем решения в MathCAD - как видно они практически идентичны: 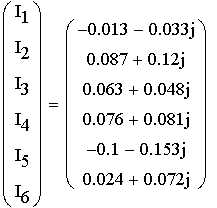 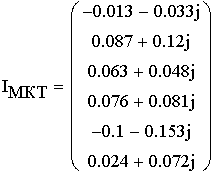 6. Определим токи в ветвях исходной схемы методом узловых потенциалов при помощи решения СЛАУ в программе MatCAD14. Положим потенциал узла №3 равным нулю: 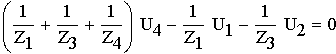    Определим токи в ветвях схемы через рассчитанные значения узловых напряжений:  Сравним данные, рассчитанные ранее и полученные путем решения в MathCAD - как видно они практически идентичны:   7. Определим методом эквивалентного генератора напряжения ток в ветви №4: Удалим из схемы источник ЭДС считая его сопротивление равным 0:  Определим сопротивление эквивалентного генератора Zг, для этого преобразуем треугольник Z2, Z5, Z6 в звезду:     Пересчитаем последовательно включенные сопротивления:  Сопротивление генератора Zг равно:  Определим напряжение генератора UГ методом контурных токов:  Выражения для сопротивлений контуров имеют вид: Выражения для сопротивлений связи между контурами имеют вид: Выражения для контурных ЭДС имеют вид: Система уравнений, составленная по методу контурных токов, имеет вид:  Решив систему уравнений, найдем значения контурных токов:   Зная значение контурных токов, определим напряжение эквивалентного генератора: Определим значение тока в ветви №4:  По полученному результату можно сказать, что расчет произведен верно, так как расcчитанное значение тока совпадает с полученным ранее. 8. Занесем полученные данные в таблицу: 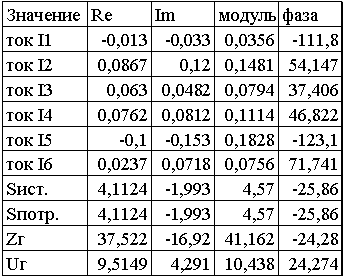 9. Построим векторную диаграмму токов и напряжений: 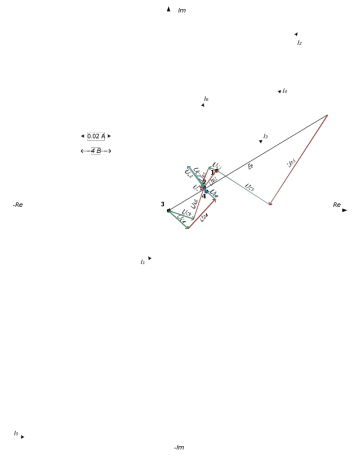 |
