конспект ТОЕ. Конспект ТОЕ У частина. 1. Трифазний генератор З'єднання в зірку й трикутник, фазні й лінійні величини
 Скачать 1.93 Mb. Скачать 1.93 Mb.
|
Трифазні ланцюги. Симетрична трифазна система ЕРС. Схеми з’єднання обмоток генератораПлан 1.Трифазний генератор2.З'єднання в зірку й трикутник, фазні й лінійні величиниТрифазні ланцюги знайшли широке поширення в електропостачанні промисловості, транспорту й сільського господарства внаслідок їх економічних і енергетичних достоїнств. Під трифазним ланцюгом (системою) розуміють сукупність трифазного джерела (генератора), навантаження й сполучних проводів. Трифазний генераторВідомо, що при обертанні провідника в рівномірному магнітному полі в ньому наводиться ЭДС З 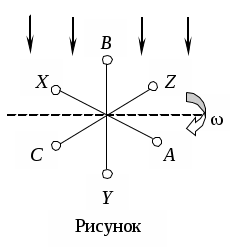 акріпимо жорстко на одній осі три однакові котушки (обмотки), зміщені відносно один одного в просторі на акріпимо жорстко на одній осі три однакові котушки (обмотки), зміщені відносно один одного в просторі на При цьому в котушці A буде наводитися Такого ж значення ЭДС виникнуть у котушках B і C, але відповідно через 120 і 240 після початку обертання, тобто Сукупність трьох котушок (обмоток), що обертаються на одній осі з кутовою швидкістю , у яких наводяться ЕРС, рівні по модулі й зрушені друг від друга на кут 120 називають симетричним трифазним генератором. Кожна котушка генератора – це фаза генератора. У генераторі на рисунку фаза B «треба» за фазою A, фаза C – за фазою B. Така послідовність чергування фаз називається прямою послідовністю. При зміні напрямку обертання генератора буде мати місце зворотна послідовність чергування фаз. Прямої послідовності на підставі співвідношень (2, 3) відповідає векторна діаграма ЕРС, зображена на рисунку, а, для зворотної - векторна діаграма ЕРС нарисунку. Надалі всі міркування з розрахунку трифазних ланцюгів будуть стосуватися тільки трифазних систем із прямою послідовністю проходження генераторних ЕРС. П 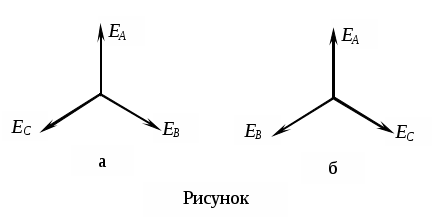 ерейдемо від миттєвих значень ЕРС до їхніх комплексів: 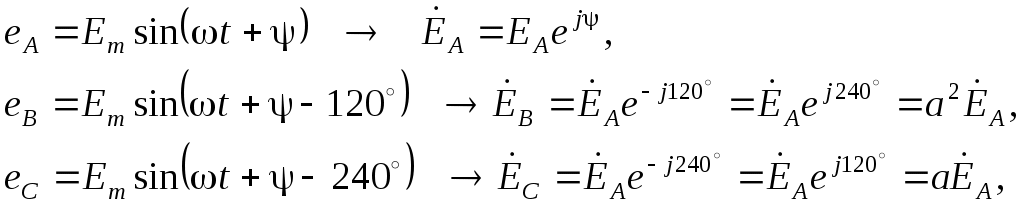 де оператор повороту Сумі миттєвих ЕРС відповідає сума комплексів цих ЭДС. Г 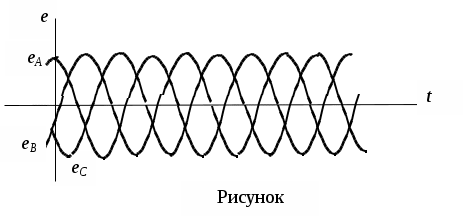 рафік зміни миттєвих значень ЕРС при = 90 представлений на рисунку щомиті алгебраїчна сума ЕРС дорівнює нулю. Крайним точкам котушок (обмоток) дають назва кінець і початок. Початку котушок позначають A, B, C, кінці відповідно X, Y, Z (рисунок, а). Фазні обмотки трифазного генератора можуть бути зображені у вигляді джерел ЕРС З 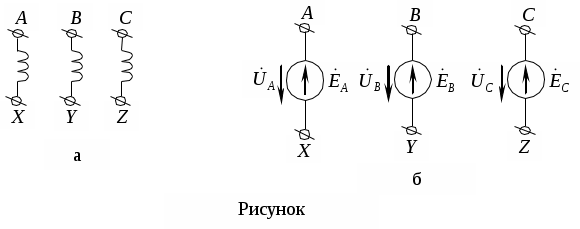 'єднання в зірку й трикутник, фазні й лінійні величини У трифазних ланцюгах застосовують два види з'єднань генераторних обмоток - у зірку й трикутник (рисунок) П 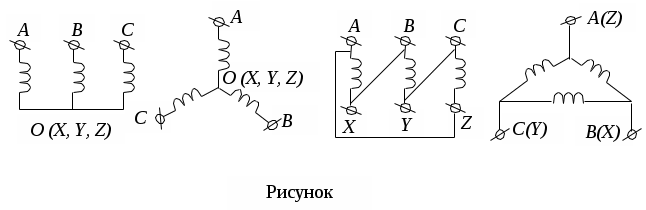 ри з'єднанні в зірку всі кінці фазних обмоток з'єднують в один вузол, називаний нейтральною або нульовою крапкою, і позначають, як правило, буквою O. При з'єднанні в трикутник обмотки генератора з'єднують так, щоб початок однієї з'єднувалося з кінцем іншої. ЕРС у котушках у цьому випадку позначають відповідно У 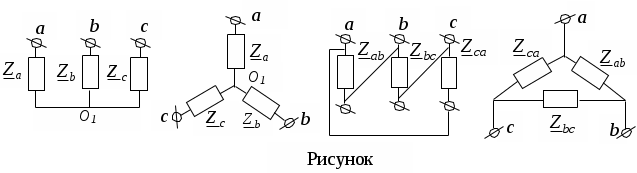 зірку й трикутник включаються й опору навантаження так, як показано на рисунку. Фазні опори Існує п'ять видів з'єднання генераторів з навантаженням: зірка – зірка з нульовим проведенням, зірка – зірка без нейтрального проведення, трикутник – трикутник, зірка – трикутник і трикутник – зірка (рисунок). Сполучні проведення між початками фаз навантаження й початками фаз генератора називають лінійними проводами. Як правило, початку фаз генераторів позначають заголовними буквами, а навантаження – прописними. Проведення, що з'єднує нульові крапки генератора й навантаження, називають нульовим або нейтральним проведенням. Напрямок струмів у лінійних проводах прийнято вибирати від генератора до навантаження, а в нульовому – від навантаження до генератора. На рисунку Лінійні напруги (напруги між лінійними проводами) - це різниця відповідних фазних напруг Лінійні струми при прийнятих напрямках струмів (рисунок) визначаються по першому законі КІрхгофа Таким чином, фазні напруги на генераторі – це напруги, прикладені до обмоток генератора Сукупність відповідної фази генератора, сполучного проведення й фази навантаження називають фазою трифазного ланцюга. (Не плутати з початковою фазою гармонійної функції!). 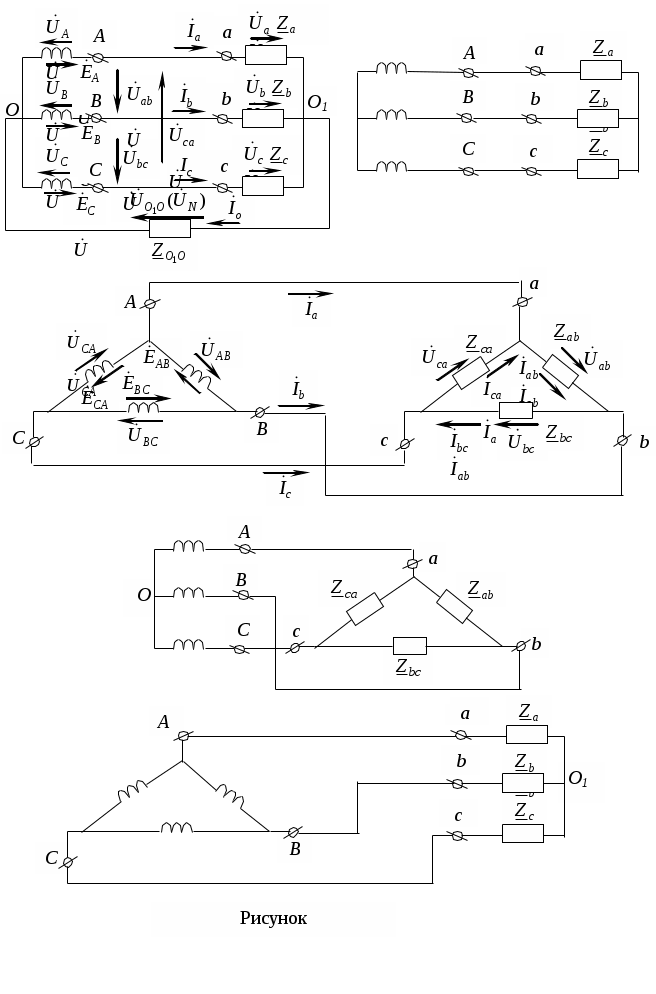 Тема: Розрахунок параметрів трифазних ланцюгівРозглянемо розрахунок трифазного ланцюга зірка – зірка з нейтральним проведенням (мал. 1.7). Розрахунок такого ланцюга можна робити всіма відомими методами розрахунку розгалужених ланцюгів. Найчастіше раціонально застосовувати метод вузлових потенціалів, тому що в цій схемі два вузли O і O1, ідля визначення невідомих струмів і напруг потрібно скласти одне рівняння. Приймемо потенціал крапки Про рівний нулю, тоді напруга нейтрали Тут Напруга на фазах навантаження 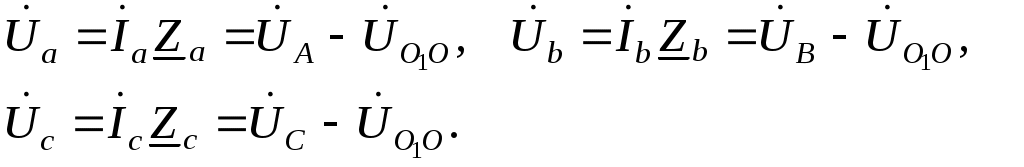 Струми у фазах: Розглянемо кілька приватних випадків. Відсутнє опір у нейтральному проведенні Опору навантаження однакові Векторні діаграми напруг на навантаженні й на генераторі збігаються й мають вигляд, представлений на рисунку, а. П 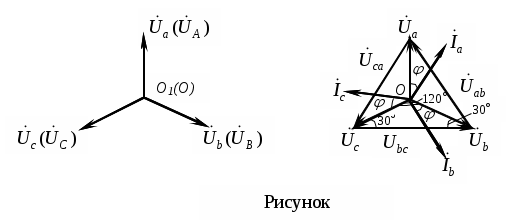 ри активно-індуктивному характері навантаження >0, векторні діаграми струмів і напруг на навантаженні показані на рисунку, б. З огляду на співвідношення між фазними й лінійними напругами, одержимо, з'єднуючи відповідні крапки aз b,bзc,cз a,лінійні напруги Розрахувавши трикутник, утворений, наприклад, фазними напругами Тут Нейтральне проведення відсутній, що відповідає схемі «зірка – зірка без нейтрального проведення». Розрахунок виконується по формулах з обліком того, що Зауваження. У схемі «зірка - зірка без нейтрального проведення» із симетричним генератором і несиметричним навантаженням у випадку рівності комплексних опорів тільки у двох фазах напруга нейтрали можна визначити зі співвідношень 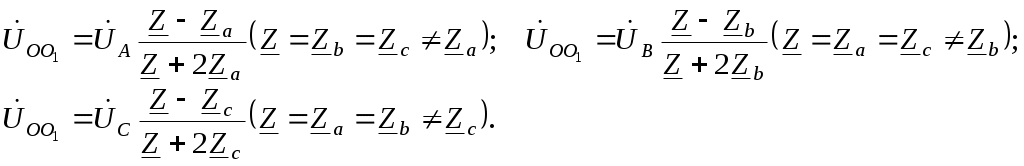 Покажемо справедливість цих формул на прикладі 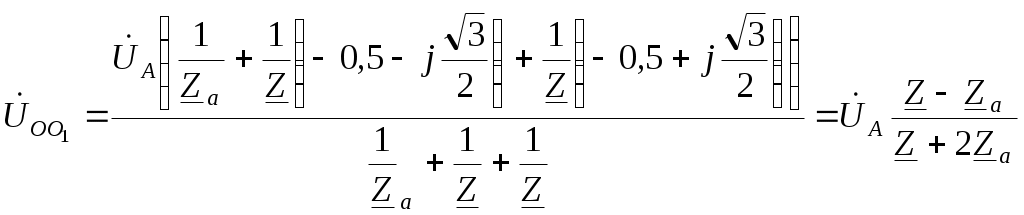 При з'єднанні навантаження в трикутник струми в його фазах визначаються за законом Ома Лінійні струми знаходять по першому законі Кірхгофа О 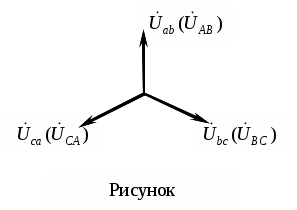 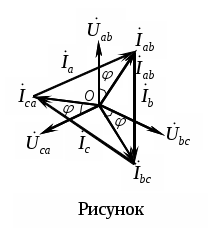 скільки лінійні напруги на навантаженні дорівнюють лінійним напругам на генераторі, які у свою чергу рівні відповідної ЕРС на обмотках генератора, векторна діаграма лінійних напруг на навантаженні (рисунок) повністю збігається з векторною діаграмою генераторних ЕРС, наведених на рисунку. скільки лінійні напруги на навантаженні дорівнюють лінійним напругам на генераторі, які у свою чергу рівні відповідної ЕРС на обмотках генератора, векторна діаграма лінійних напруг на навантаженні (рисунок) повністю збігається з векторною діаграмою генераторних ЕРС, наведених на рисунку.Нехай навантаження симетричне й носить активно-індуктивний характер, тоді векторні діаграми напруг, фазних і лінійних струмів мають вигляд, представлений нарисунку. За допомогою отриманої діаграми можна визначити, що модулі лінійних струмів рівні (вони є сторонами рівностороннього трикутника) 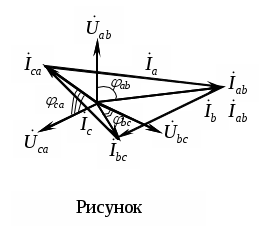 . .З розрахунку трикутників, утворених двома фазними струмами (бісектриси рівностороннього трикутника) і лінійним струмом, треба, що При несиметричному навантаженні векторні діаграми струмів мають найрізноманітніший вид. Приклад такої діаграми наведений на рисунок, де Деякі приватні режими роботи трифазних ланцюгівР 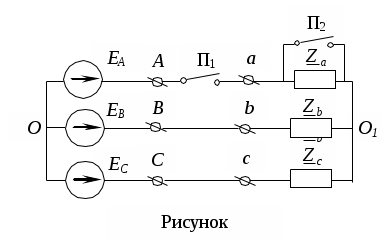 озглянемо приватні режими роботи трифазних ланцюгів на прикладі з'єднання «зірка – зірка» і з'єднання навантаження в трикутник. Розглянемо три режими роботи схеми, представленої на рисунку. 1. по величині В 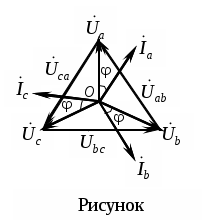 екторні діаграми при активно-індуктивному навантаженні представлені на рисунку. Всі фазні струми екторні діаграми при активно-індуктивному навантаженні представлені на рисунку. Всі фазні струми 2  . Перемикачі П1 і П2 розімкнуті (режим холостого ходу або обрив фази А). При цьому схема із трифазного ланцюга перетвориться в однофазну з напругою . Перемикачі П1 і П2 розімкнуті (режим холостого ходу або обрив фази А). При цьому схема із трифазного ланцюга перетвориться в однофазну з напругою Векторні діаграми представлені на рисунку. Струм в опорах 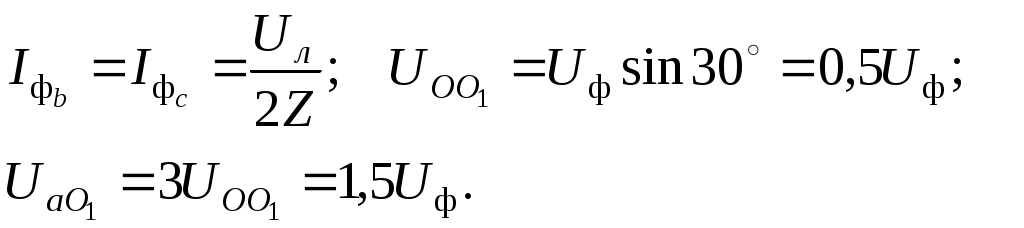 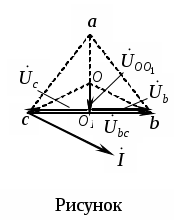 Таким чином, фазний струм і фазна напруга неушкоджених фаз зменшилося в 3 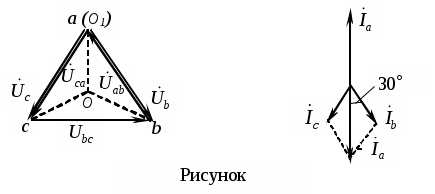 . Перемикачі П1 і П2 замкнуті (режим короткого замикання фази А). Потенціал крапки ПРО1приймає значення потенціалу крапки a. Векторні діаграми представлені на рисунку. У цьому режимі Таким чином, фазні напруги й струми неушкоджених фаз B і C збільшилися в Н 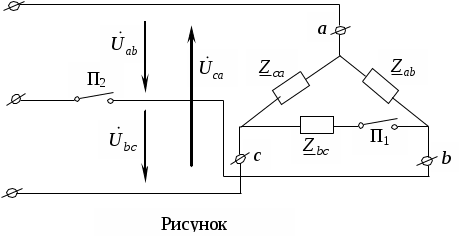 а рисунку наведена схема, що складається із трьох однакових опорів 1. Перемикачі П1 і П2 замкнуті. При цьому має місце симетричний режим роботи трифазного ланцюга. В 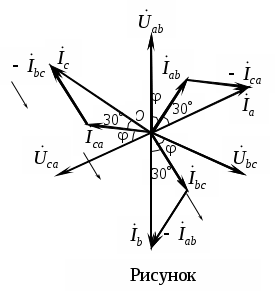 екторні діаграми напруг і струмів при активно-індуктивному навантаженні наведені на рисунку. екторні діаграми напруг і струмів при активно-індуктивному навантаженні наведені на рисунку.Всі фазні струми 2. Перемикач П1 розімкнуть (режим холостого ходу або обрив фази bc). Л 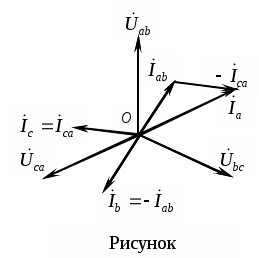 інійні струми інійні струми 3. Перемикач П1 замкнуть, а перемикач П2 розімкнуть (обрив лінії В). При цьому трифазний ланцюг перетвориться в однофазну, і всі три опори підключаються до напруги С 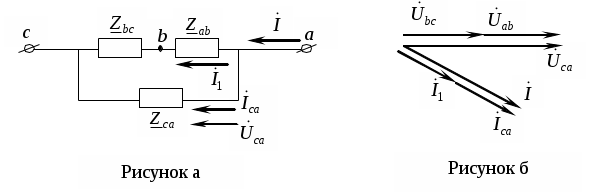 трум, що протікає по двох опорах Таким чином, при обриві лінійного проведення у фазах, гальванічно пов'язаних з ним, струми зменшуються у два рази, у третій фазі струм залишається незмінним, лінійний струм у неушкодженій лінії зменшується в порівнянні із симетричним режимом в 1,15 рази. Вираження фазних напруг трифазної системи зірка – зірка без нейтрального проводу через лінійну напругуУ схемі на рисунку у загальному випадку По першому законі Кірхгофа В 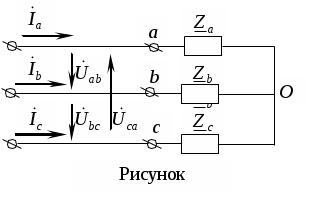 иразимо иразимо Підставимо ці вираження Звідси Заміняючи в відповідно Потужності в трифазних ланцюгахПотужності в трифазних ланцюгах розраховуються так само, як і потужності в розгалужених гармонійних ланцюгах. Потужність трифазного генератора, з'єднаного в трикутник Для зірки Потужності споживачів, з'єднаних у трикутник Для зірки Тут У симетричних трифазних ланцюгах 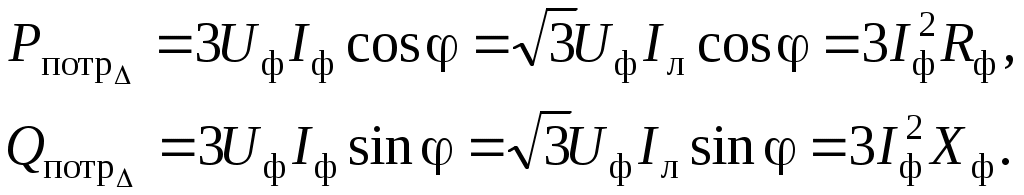 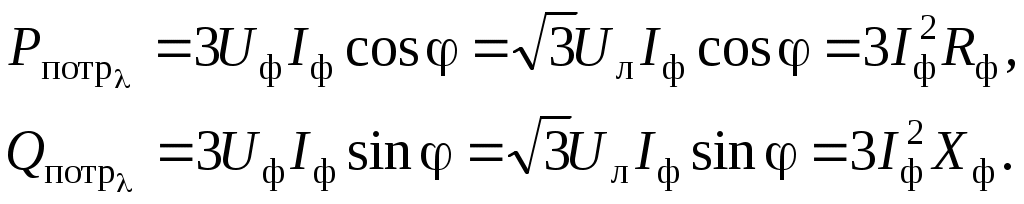 Кругове обертове магнітне поле трифазного струмуП  ри протіканні по котушці струму в напрямку, зазначеному на мал. 1.24, вектор магнітної індукції ри протіканні по котушці струму в напрямку, зазначеному на мал. 1.24, вектор магнітної індукції При зміні струму за синусоїдальним законом Р 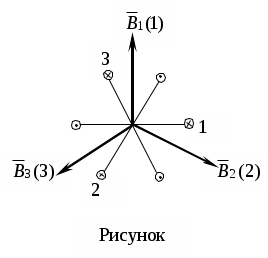 озмістимо три (1, 2, 3) однакові котушки, зрушені в просторі на 120 друг щодо друга (рисунок). озмістимо три (1, 2, 3) однакові котушки, зрушені в просторі на 120 друг щодо друга (рисунок).Приймемо за позитивний напрямок векторів Проаналізуємо, чому буде рівнятися сума При Векторна діаграма векторів При Векторна діаграма векторів При В 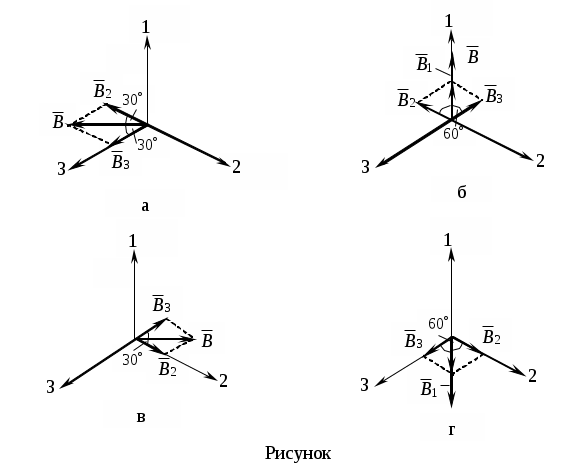 екторна діаграма векторів При Для цього моменту справедлива векторна діаграма Із представленого аналізу треба, що при підключенні трифазного ланцюга до трьох однакових котушок, зрушеним відносно один одного в просторі на 120, виникає обертове магнітне поле. Вектор магнітної індукції такого поля по модулі дорівнює 1,5Bmі обертається з кутовою швидкістю . Ефект обертового магнітного поля використається для створення асинхронних і синхронних трифазних двигунів. |
