Туынды. 9. Туынды. 1. туынды оыту Дlстемесl Жоспары. Туынды ымын енгізу туралы жалпы мселелер Туынды ымына келтірілетін есеп
 Скачать 270.52 Kb. Скачать 270.52 Kb.
|
|
1. ТУЫНДЫ ОҚЫТУ ӘДlСТЕМЕСl Жоспары. 1.Туынды ұғымын енгізу туралы жалпы мәселелер 2. Туынды ұғымына келтірілетін есеп 3. Ұғымға атау беру 4. Туындының анықтамасы және оның геометриялық мағынасы 5. Функцияның туындысын табу алгоритмі 6. Туынды табу ережелері 1.Туынды ұғымын енгізу туралы жалпы мәселелер Туынды мен интегралды енгiзудiң әр түрлi тәсiлдерi көп жағдайларда функцияның нүктедегi шегi ұғымына байланысты. Қазiргi кездегi математикада, әдетте туынды ұғымы мен интеграл ұғымы функцияның нүктедегi шегi ұғымына байланысты анықталады.. 1981 және 1985 жылғы қабылданған бағдарламалар функцияның нүктедегi шегiн арнаулы тақырып ретiнде қарастырмайды, сөйтiп туынды және интеграл ұғымдарын шек ұғымын айқын түрде қолданбай өтуге негiзделген болатын. Оның сенбебі де бар еді. Математикада алдымен туынды және интеграл ұғымдары тұжырымдалған, ал кейiннен бұл ұғымдарды жалпылау нәтижесiнде функцияның шегi ұғымы пайда болғаны белгiлi. Туынды мен интегралды оқытудың бұл тәсiлiн шартты түрде тарихи тәсiл деп есептейдi. Мектеп оқулықтарында туынды мен интеграл ұғымдарын мұндай тәсiлмен енгiзу орта мектептегi туындыны оқытудың теориялық емес, практикалық аспектiлерiне баса назар аударуды көздейдi. Ал қазіргі кездегі мектеп оқулықтарында туынлды шек ұғымы арқылы енгізіледі. Сондықтан орта мектепте туындыны оқыту мынадай ретпен жүзеге асырылады: 1) туынды ұғымының физикалық немесе геометриялық мағынасын анықтайтын есеп қарастырылады; 2) туынды ұғымына атау беру; 3) туынды ұғымының анықтамасын тұжырымдау, оның геометриялық мәнiн түсіндіру; 4) функцияның туындысын табу алгоритмін көрсету; 5) туынды табу ережелер; 6) туындының қолданылуы. 2. Туынды ұғымына келтірілетін есеп Қозғалыстағы дененiң, белгiлi бiр мезеттен бастап t уақыттың iшiнде жүрген жолын S деп белгiлесек, t-ның өзгеруiне S-тiң оған белгiлi мәнi сәйкес келетiн болады. Сондықтан жүрген жол өткен уақыт t-ның функциясы, яғни S=f(t) болады. Бұл теңдеу қозғалыстың теңдеуi немесе қозғалыс заңы деп аталады. Осы берiлген қозғалыс заңына сүйенiп, дененiң берiлген уақыт мезетiндегi жылдамдығын табу керек болсын. Ол үшiн қозғалыстағы дененiң берiлген t уақыт мезетiндегi жылдамдығы деп ненi айтамыз, сонны анықтайық. Берiлген t уақыт мезетiнен кейiн, тағыда бiраз уақыт өтсiн, оны t деп белгiлейiк. Осы аз уақыттың iшiнде қозғалыстағы дене S жол жүрсiн. Сонда  . .t неғұрлым аз болса, орташа жылдамдық соғұрлым аз өзгередi де t уақыт мезетiндегi дененiң қозғалысын дәлiрек анықтайды. Сондықтан мынадай анықтама бере аламыз. Анықтама. Қозғалыстағы дененiң t уақыты мезетiндегi жылдамдығы деп,  . .Қозғалыстағы дененiң берiлген уақыты мезетiндегi жылдамдығын табу үшiн осы шектi табу керек. Декарттың координаталар жүйесiнде у=f(х) теңдеумен берiлген үзiлiссiз АВ сызығына оның М0(х0;у0) нүктесiнде жүргiзiлген жанаманы анықтау керек болсын. Ол үшiн аргумент х-ке х өсiмше берiп, у-тiң оған сәйкес өсiмшесiн y деп белгiлейiк. Қисық бойындағы (х0+  Анықтама.АВ қисығына М0(х0;у0) нүктесiнде жүргiзiлген жанама деп, нүктесi қисық бойымен М0 нүктесiне шексiз жақындағандағы М0 қиюшысының М0Т түрiндегi орналасуын айтамыз (3-сурет). Е  ндi берiлген анықтамаға сүйенiп, М0Т жанаманың теңдеуiн қорытып шығарайық. Жанама берiлген жанасу нүктесi М0(х0;у0) арқылы өтедетін түзу, сондықтан жанаманың теңдеуiн былайша жазуға болады: ндi берiлген анықтамаға сүйенiп, М0Т жанаманың теңдеуiн қорытып шығарайық. Жанама берiлген жанасу нүктесi М0(х0;у0) арқылы өтедетін түзу, сондықтан жанаманың теңдеуiн былайша жазуға болады: у-у0=k(х-х0). Демек, жанаманың теңдеуiн табу үшiн бұрыштық коэффицентiн k=tg-нi табу керек,  . (х0+ . (х0+ . .Екiншi жағынан у=f(х)функциясы үзiлiссiз болғандықтан, хнөлге ұмтылғанда унөлге ұмтылады. Онда х0 ұмтылғанда Nнүктесi М0нүктесiне ұмтылады. Ендеше  немесе  . .Сондықтан жанаманың теңдеуi мына түрде жазылады:  . .Сөйтiп, жанаманың теңдеуiн жазу үшiн  шегiн табу керек. Ал шегiн табу керек. Ал ; ;Демек, жанаманың теңеуi: Геометриялық тұрғыдан алып қарағанда функцияның туындысы сол функция мен кескiнделетiн қисыққа жүргiзiлген жанаманың бұрыштық коэффициентi. Кейбір оқулықтарда алдымен туынды ұғымына келтіретін қисыққа жүргізілген жанама туралы есепті алдымен қарастырады да, одан кейін жылдамдық туралы есепке көшеді. Бұдан келiп туындының анықтамасы берiледi. Көрсетiлген екi есептiң шешуiнен мынаны байқаймыз: Бұл есептердiң бiрiмен бiрiнiң байланысы жоқ. Бiрiншiсi – физикалық есеп. Ал екiншiсi –. таза геометриялық есеп Бiрақ бұл есептердiң шешiмдерi математикалық тұрғыдан алып қарағанда бiрдей, шектерге келтiрiлдi. Екеуiнде де функция өсiмшесiнiң аргумент өсiмшесiне қатынасының, аргумен төсiмшесi нөлге ұмтылғандағы шегiн табу керек. Мұндай есептердi туындыны анықтауға берiлген есептер дейдi. Сол себептен де жоғарыдағы қарастырылған есептердi туынды ұғымына келтiретiн немесе туынды ұғымын түсiнуге арналған есептер делiнедi. Бiз тек екi есеп қана қарастырдық, ал мұндай есептер жаратылыстану ғылымы мен техникалық алуан түрлi салаларда көп кездеседi. Ендi функция туындысының жалпы анықтамасына көшуге болады. Жоғарыда көрсетiлген есептердiң шешулерiн ендi былай жазуға болады:  ; ;Жолдың уақыт бойынша алынған туындысы жылдамдық, осы сияқты  , яғни жылдамдықтан уақыт бойынша алынған туынды үдеу болады. Бұл туындының физикалық мағыналары. , яғни жылдамдықтан уақыт бойынша алынған туынды үдеу болады. Бұл туындының физикалық мағыналары. . .Демек, жанаманың теңеуi: Геометриялық тұрғыдан алып қарағанда функцияның туындысы сол функция мен кескiнделетiн қисыққа жүргiзiлген жанаманың бұрыштық коэффициентi. 3. Ұғымға атау беру Математикада мынадай терминология қабылданған: дененiң t0 уақыт мезетiндегi орташа жыдамдығын функцияның t0 нүктесiндегi туындысы деп атайтын боламыз. Физикалық тұрғыдан алып қарағанда лездiк жылдамдық S(t) жолының t0 уақыт мезетiндегi өзгеру жылдамдығын сипаттайды. Математикалық тұрғыдан алып қарайтын болсақ, S(t) функциясының туындысы S(t) функциясының мәндерiнiң t0 нүктесiндегi өзгеру жылдамдығын көрсетедi. Әдетте нақтылы үдерістер бiрқалыпты түрде өтпейдi. Мысалы, қыздырылып жатқан металл стерженнiң ұзындығының өзгеру үдерісі қарастырылсын. Бұл үдеріс бiрқалыпты емес: алдымен, стерженнiң ұзындығы шамалы ғана өзгередi, одан кейiн стерженнiң ұзындығы тездеп ұзара бастайды. Келесi мысал: айталық, бiр ыдыстың төменгi жағындағы тесiктен сұйық ағатын болсын. Ағатын сұйықтың жылдамдығы уақыттың өзгеруiне байланысты кеми бастайды. Бiр клеткалы организмдердiң бөлiну үдерісін алсақ оның жылдамдығы тез өседi. Әрбiр осындай есептердi шығару кезiнде орташа жылдамдықтың шегiн табу есебiмен кездесемiз. f(x) параметрiнiң өзгерiсiнiң орташа жылдамдығын анықтау үшiн осы параметрдiң х өсiмшесiне сәйкес келетiн өсiмшесiн жазып,  қатынасын құру керек. Сонда х0 мезетiндегi өзгеру жылдамдығы қатынасын құру керек. Сонда х0 мезетiндегi өзгеру жылдамдығы  шегi арқылы анықталады, оны былай да жазуға болады: шегi арқылы анықталады, оны былай да жазуға болады: . . f(x) параметрiнiң x0 мезетiндегi өзгеру жылдамдығы бұл f(x) параметрiнiң х0 нүктесiндегi туындысы. 4. Туындының анықтамасы және оның геометриялық мағынасы Енді функцияның берiлген нүктедегi туындысының анықтамасын тұжырымдап айтуға болады. Ол үшін мынадай математикалық терминдер қолданылады: функция, функцияның өсiмшесi, аргументтiң өсiмшесi, қатынас, қатынастың шегi. Туындының анықтамасы. Егер функция өсiмшесiнiң аргумент өсiмшесiне қатынасының аргумент өсiмшесi  . .Туындының х аргумент бойынша алынаған болса, оны Туындының анықтамасынан f(x) функциясының х0 нүктесiндегi туындысы дегенiмiз: 1) x0-дағы, 2)  қатынасының шегi; 3) сан болатандығы оқушыларға айтылу керек. қатынасының шегi; 3) сан болатандығы оқушыларға айтылу керек. Бiз жоғарыда туындының анықтамасын оның физикалық мағынасына сүйенiп, қозғалыстағы дененiң орташа жылдамдығын табу туралы механикалық есептi шығаруға байланысты анықтадық. Туынды ұғымын қисықтың берiлген нүктесiне жүргiзiлген жанаманың теңдеуiн құру туралы геометриялық есепке сүйенiп те анықтауға болады. 5. Функцияның туындысын табу алгоритмі Туындының анықтамасы тұжырымдалып айтылғаннан кейін мынадай сұрақ туындайды: «f(x) функциясының х0 нүктесiндегi туындысын қалай табуға болады?» Бұл сұрақтың жауабы мынадай алгоритмдер арқылы жүзеге асырылады: 1) аргументi x=x0-ге x өсiмше беріледі:  ; ; 2) f(x) функциясының х0 нүктесiндегi өсiмшесi табылады: f(x0)=f(x0+x)–f(x0); 3)  қатынасын құрамыз; қатынасын құрамыз; 4) осы функцияның x0-дағы шегi Нақтылау мақсатында туындыны табуға берiлген бiрiншi мысалды екi деңгейде орындаған тиiмдi: 1) х0-ге нақтылы сан, мысалы, x0=2 берiп, 2) x0-ды жалпы түрде алып. «Функцияның туындысы» мен «функцияның нүктедегi туындысының» айырмашылықтары түсiндiрiледi: функцияның туындысының x0 нүктесiндегi мәнi сан, ал функцияның туындысы функция болады. Анықтаманы пайдаланып функциялардың туындысын табайық: Мысал. 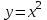 функциясының туындысын есептеу. функциясының туындысын есептеу.1 . 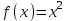 . .2.  . .  5.  Сонымен,  . .Мысал.  функциясының туындысын есептеу. функциясының туындысын есептеу.1. ƒ(x)=  , мұнда , мұнда  2.  х;х+ х;х+ х; х;  3.  ƒ= ƒ= 4. 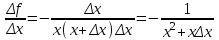 5.   Сонымен, f/(x)=  . .Мысал. 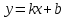 функциясының туындысын есептеу. функциясының туындысын есептеу.1.  аргументi үшiн аргументi үшiн  . .2.  3.  4. 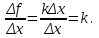 5.  Сонымен,  Мысал. 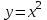 функциясына (1,1) нүктесінде жүргізілген жанама теңдеуін жазу. функциясына (1,1) нүктесінде жүргізілген жанама теңдеуін жазу.Шешуі: 1 Түзудің жалпы теңдеуін 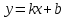 түрінде жазып аламыз. түрінде жазып аламыз.2 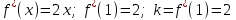 3 Түзу (1,1) нүктесінен өтетіндіктен, 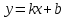 теңдеуінен теңдеуінен 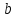 -ны табамыз: 1=2·1+ -ны табамыз: 1=2·1+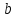 , бұдан , бұдан 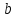 = -1. = -1. Сонымен, жанаманың теңдеуі  . .Мысалы, у = х3функциясы үшін 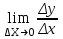 табайық. Жоғарыдағытүсініктерге сүйенсек: табайық. Жоғарыдағытүсініктерге сүйенсек: 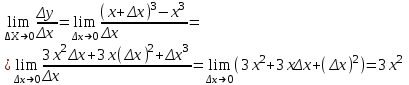 6. Туынды табу ережелері Жоғарыда келтірілген туындыны есептеу алгоритмінен дифференциалдау ережелері мен формулаларын шығарып алуға болады: 1. Тұрақты шаманың туындысы нөлге тең. С тұрақты шама.  болғанда, болғанда, 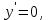 мұны кейде былай мұны кейде былай жазады:  2. Тұрақты көбейткішті туындының алдына шығарып жазуға болады.  болса ( болса ( - тұрақты көбейткіш), - тұрақты көбейткіш),  болады. болады. 3 Алгебралық қосындының туындысы сол функциялардың туындыларының сәйкес алгебралық қосындысына тең болады. 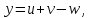 ал ал    өздері х-ке тәуелді функциялары болсын. Сонда: өздері х-ке тәуелді функциялары болсын. Сонда:  4 Екі функцияның көбейтіндісінің туындысын табу үшін бірінші функцияның туындысын екінші функцияның өзіне көбейтіп, содан соң екінші функцияның туындысын бірінші функцияның өзіне көбейтіп, шыққан екі көбейтіндінің қосындысын алу керек. 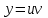 болсын. Сонда: болсын. Сонда:  Мұны былай да жазады: Мұны былай да жазады:  5. Екі функциядан құралған бөлшектің туындысын табу үшін алымындағы функцияның туындысын бөліміндегі функцияның өзіне көбейтіп, содан соң бөліміндегі функцияның туындысын алымындағы функцияның өзіне көбейтіп, алдыңғы көбейтіндіден соңғы көбейтіндіні шегеріп, одан әрі осыдан шыққан айырманы бөліміндегі функцияның квадратына бөлу керек.  болсын. болсын.   6. Күрделі  функцияларсының х бойынша туындысын табу үшін функцияларсының х бойынша туындысын табу үшін  функциясының функциясының 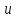 бойынша туындысын тауып, содан кейін бойынша туындысын тауып, содан кейін 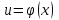 функциясының х бойынша туындысы табылады, шыққан екі туындының көбейтіндісін алу керек. функциясының х бойынша туындысы табылады, шыққан екі туындының көбейтіндісін алу керек. Мысал. у = Зх5 — 2х2 + 5х + 4функциясының туындысын табу керек. Шешуі. y'=(3x5-2x2+ 5x+4)/=3∙5x4-2∙2x+5=15x4-4x+5. Мысал.  функциясы туындысының функциясы туындысының 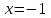 нүктесіндегі мәнін табу. нүктесіндегі мәнін табу.Шешуі:  , , Жауабы: -1,5. Мысал. y=(5x + 3)(6x2—l7x + 4)функциясының туындысын табу керек. Шeшyi. y/= (5х + 3)'. (6x2- l7x + 4) + (5x + 3) • (6x2- 17x + 4)' = 5(6x217x + 4) + (5x + 3) • (12x-17)=30x2- 85x+20+60x2-85x+36x-51=90x2-134x-31. Мысал. y =  функцияның туындысын табайық. функцияның туындысын табайық.Шешуі: Бөліндінің туындысын табудың формуласын пайдалана, отырып туындыны есептейміз:  Мысал. 1) y=(6x + 5)3 функциясынан туынды табу керек. Шешуі. Күрделі функцияның туындысының формулсы бойынша y' = 3(6х + 5)2 • (6х + 5)'=3(6x + 5)2 •6=18(6x + 5)2; 2) y = 3sin 7x; y' = 3(sin7x)' =3cos7x •(7x)/=21cos7x; 3)   Қарапайым элементар функциялар туындыларының кестесін де келтірейік: 1 2 3  . .4  . .5  . .6 Мысал. Функцияның туындысын табу:  . .Шешуі:  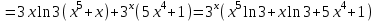 ; ;Жауабы: 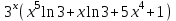 . .Енді негізгі элементар функциялардың туындылар кестесін күрделі функцияның туындысын табу ережесі бойынша жалпылай жазайық: ( 1 3 5 7 9  , 10 , 10  , 11 , 11 , 12 , 12  , ,13  , 14 , 14  , ,Жоғары ретті туындылар. Айталық Осылайша, Жалпы жағдайда, функцияның (n-1) –туындысынан алынған туындыны, оның n-туындысы деп атайды. Оны былай белгілейді: Реті бірден жоғары туындыларды жоғары ретті туындылар деп атайды. Енді туынды табуға қатысты мысалдар қарастырайық: Мысал. у = 8  функциясының туындысын табайық. функциясының туындысын табайық.Шешуі: Берілген функцияның туындысын күрделі функцияның туындысын, табу әдісі бойынша табамыз: у`=(8  )`= 8 )`= 8  (3x (3x +x+1)`∙ln 8 = 8 +x+1)`∙ln 8 = 8 ∙ (6x+1) ∙ ln 8 ∙ (6x+1) ∙ ln 8Мысал.  функциясының туындысын табайық. функциясының туындысын табайық.Шешуі (  )´ = ( )´ = ( )´ - ( )´ - ( )´ = )´ =  Мысал. y = аrссtg 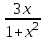 функциясының туындысын табайық. функциясының туындысын табайық. Шешуі: y´ = (аrссtg 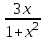 )´= - )´= - 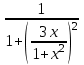 ·( ·( 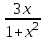 )´= - )´= - 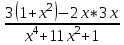 = = 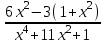 = = 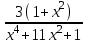 . .Мысал.  функциясының туындысын табайық. функциясының туындысын табайық.Шешуі:  Мысал.  функциясының туындысын табайық. функциясының туындысын табайық.Шешуі: Берiлген функция дәрежелi-көрсеткiштiк функция болғандықтан, теңдiктiң екi жағын да логарифмдеп, логарифмдiк туынды ережесiн қолданамыз:  . Сонда . Сонда Бұдан Бұдан  . .Мысал.  функциясы берілген. функциясы берілген.  нүктесіндегі туындыны тап. нүктесіндегі туындыны тап.Шешуі: 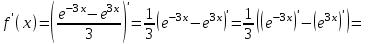 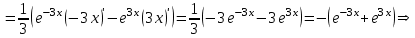 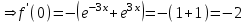 . .Жауабы: -2. Мысал. Туындыны табыңыз  . .Шешуі:   . .Жауабы:  . .Мысал. Функцияның туындысын табыңыз:  . .Шешуі:  . .Жауабы:  . .Мысал. Функцияның туындысын табыңыз:  Шешуі:   Жауабы:  . .Мысал. Функцияның туындысын табыңыз:  . .Шешуі:  формуласын қолданамыз. формуласын қолданамыз.  . .Жауабы: 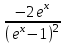 . .Мысал. у = х3 + 2х функциясының екінші ретті туындысын табу керек. Шешуі Реті бойынша, алдымен бірінші туындыны, кейін одан екінші туынды аламыз.  Мысал. 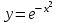 формуланың екінші ретті туындысын табу керек: формуланың екінші ретті туындысын табу керек:Шешуі Алдымен күрделі функцияң бірінші туындысын табамыз;   Содан кейін екінші туындыны алынған функциялардың көбейтіндісін дифференциялау арқылы табамыз 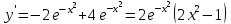 . . |
