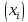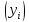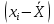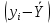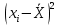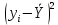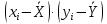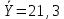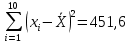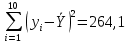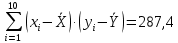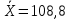Зачет, вопрос № 6 Карпова И.В.. 1. у 10 школьников изучались две характеристики х оценки iq по шкале интеллекта СтенфордаБине в шестом классе y успеваемость по химии в средней школе, оцененная на основе теста из 35 вопросов. ученика
 Скачать 45.17 Kb. Скачать 45.17 Kb.
|
|
Материалы студентки гр.34370Карповой И.В. 1. У 10 школьников изучались две характеристики: Х – оценки IQ по шкале интеллекта Стенфорда-Бине в шестом классе; Y – успеваемость по химии в средней школе, оцененная на основе теста из 35 вопросов.
Можно ли утверждать, что существует связь между этими характеристиками? Проверьте гипотезу о достоверности выборочного коэффициента корреляции. Решение: Составим вспомогательную таблицу
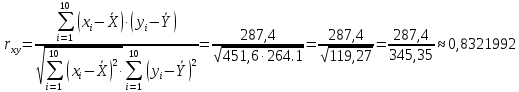 По формуле коэффициента линейной корреляции для парных сравнений : 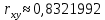 , следовательно, сила линейной связи между оценками IQ по шкале интеллекта Стенфорда-Бине в шестом классе и успеваемость по химии в средней школе высокая (положительная). , следовательно, сила линейной связи между оценками IQ по шкале интеллекта Стенфорда-Бине в шестом классе и успеваемость по химии в средней школе высокая (положительная).Проверим гипотезу о достоверности выборочного коэффициента корреляции Коэффициент линейной корреляции Пирсона 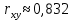 , следовательно, связь высокая (сильная). Проверим гипотезу , следовательно, связь высокая (сильная). Проверим гипотезу 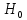 : связь отсутствует. ( : связь отсутствует. (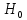 генеральный коэффициент корреляции равен 0 (в генеральной совокупности нет корреляционной связи); генеральный коэффициент корреляции равен 0 (в генеральной совокупности нет корреляционной связи); 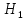 генеральный коэффициент корреляции отличен от 0). генеральный коэффициент корреляции отличен от 0).Объем выборки 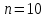 . .Эмпирическое значение критерия 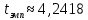 Число степеней свободы 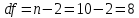 Табличное значение t-критерия Стьюдента на уровне значимости 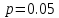 при при 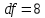 : :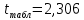 . .  , следовательно, гипотезу , следовательно, гипотезу 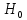 отклоняем на уровне значимости 0,05 (т.е. коэффициент линейной корреляции rху значимо отличается от 0) отклоняем на уровне значимости 0,05 (т.е. коэффициент линейной корреляции rху значимо отличается от 0)Вывод: наличие заметной корреляционной связи величин в генеральной совокупности подтверждается с доверительной вероятностью 95% (вероятность ошибки вывода составляет 5%). 2. Для проведения эксперимента необходимо, чтобы у испытуемых был примерно одинаковый коэффициент IQ. Тестирование по методике Айзенка показало следующие результаты: 105, 117, 110, 100, 112. Можно ли проводить эксперимент с данной группой?
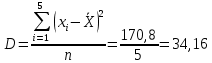 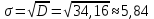  Вывод: 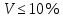 значит степень разброса данных незначительная (низкая). Из этого следует, что проводить эксперимент с данной группой можно. значит степень разброса данных незначительная (низкая). Из этого следует, что проводить эксперимент с данной группой можно. |