билеты по геометрии 9 класс новые. 1. Углы, образованные при пересечении двух параллельных прямых третьей прямой и их свойства

• Название: 1. Углы, образованные при пересечении двух параллельных прямых третьей прямой и их свойства
• Дата: 10.05.2022
• Размер: 2.39 Mb.
• Имя файла: билеты по геометрии 9 класс новые.doc
• Тип: Документы; #520725

Билет № 1

1. Углы, образованные при пересечении двух параллельных прямых третьей прямой и их свойства.

2. Треугольник: определение и виды. Теорема косинусов. Теорема синусов (доказательство по выбору учащихся)

3.1. Найдите диагонали равнобедренной трапеции, основания которой равны 4 см и 6 см, а боковая сторона равна 5 см.

3.2. В угол C величиной 83° вписана окружность с центром O, которая касается сторон угла в точках A и B. Найдите угол AOB. Ответ дайте в градусах.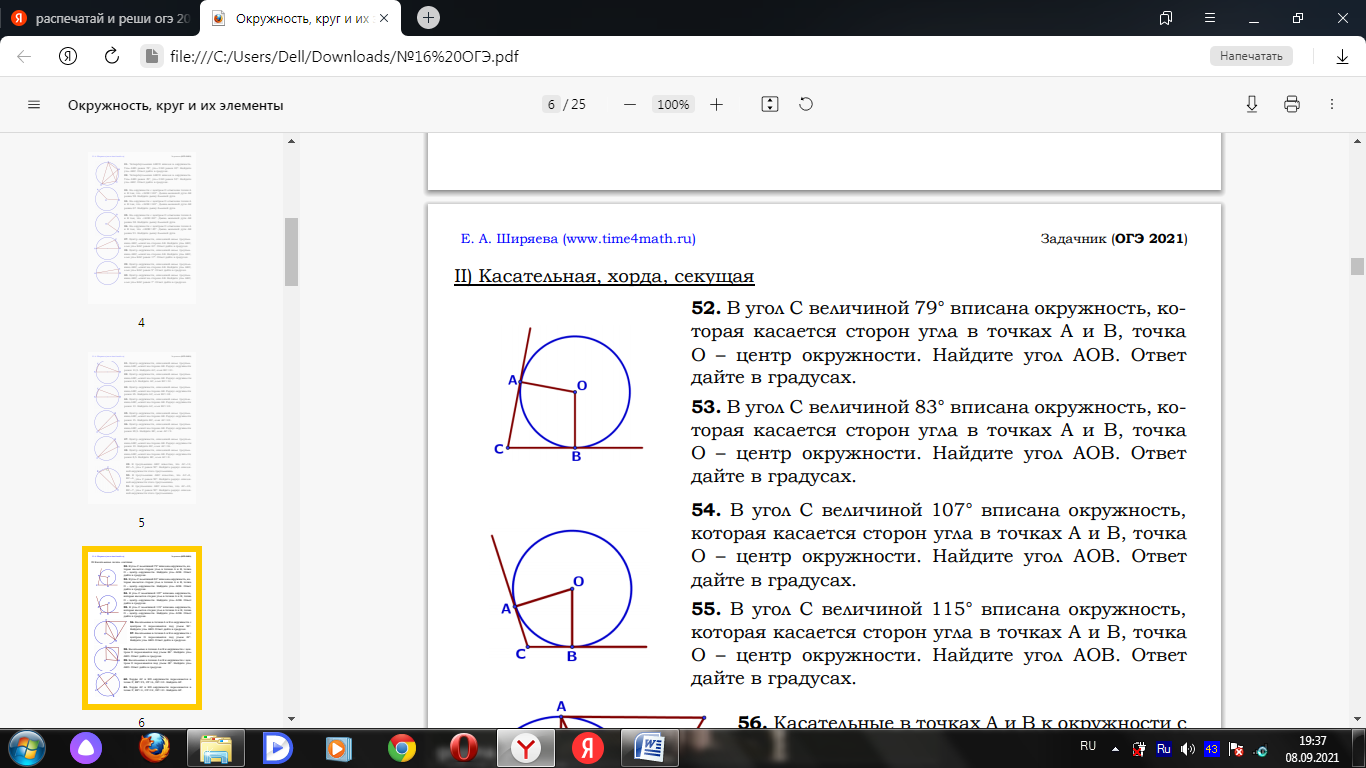



3.3. Диагональ  AC  па­рал­ле­ло­грам­ма  ABCD  об­ра­зу­ет с его сто­ро­на­ми углы, рав­ные 30° и 45°. Най­ди­те боль­ший угол параллелограмма.

4.1. Отрезки и лежат на параллельных прямых, а отрезки и пересекаются в точке . Найдите , если , , .

4.2. Внутри параллелограмма ABCD выбрали произвольную точку E . Докажите, что сумма площадей треугольников BEC и AED равна половине площади параллелограмма.

Билет № 2

1. Смежные и вертикальные углы: определение и свойство.

2. Параллелограмм. Формулы площади параллелограмма. Вывод формулы площади параллелограмма (одной по выбору учащегося).

3.1. На окружности отмечены точки A и B так, что меньшая дуга AB равна 66°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.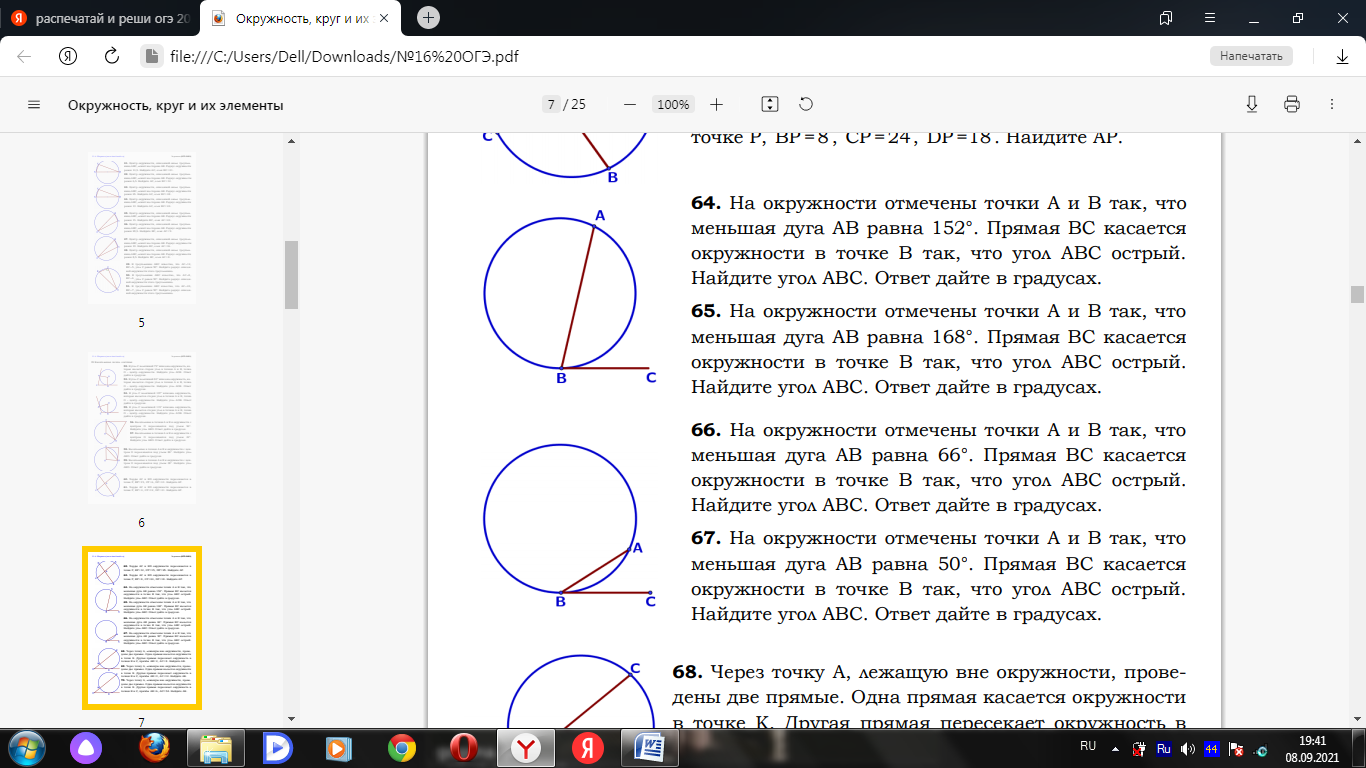



3.2. Найдите острый угол параллелограмма , если биссектриса угла образует со стороной угол, равный 41°. Ответ дайте в градусах.

3.3. В тре­уголь­ни­ке ABC AB = BC = 53, AC = 56. Най­ди­те длину ме­ди­а­ны BM.

4.1. Катеты прямоугольного треугольника равны 18 и 24. Найдите высоту, проведѐнную к гипотенузе.

4.2. Основания BC и AD трапеции ABCD равны соответственно 5 и 20, BD = 10.Докажите,что треугольники и подобны.

Билет № 3

1. Взаимное расположение прямых. Параллельные и перпендикулярные прямые: определение и свойства.

2. Прямоугольный треугольник. Теорема Пифагора (доказательство).

3.1. Точка O – центр окружности, на которой лежат точки A, B и C. Известно, что ABC=69° и OAB=48°. Найдите BCO. Ответ дайте в градусах.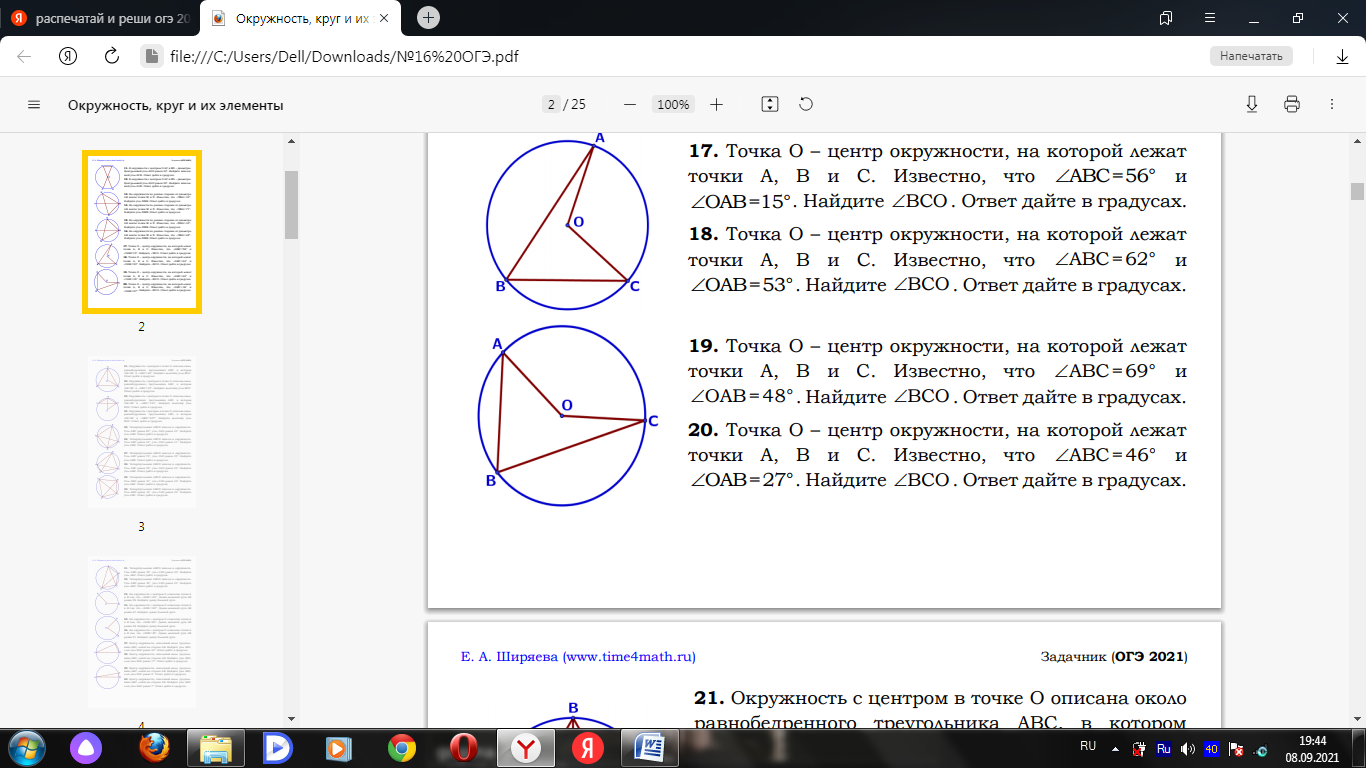



3.2. Биссектриса равностороннего треугольника равна . Найдите сторону этого треугольника.

3.3. В тре­уголь­ни­ке ABC AC = BC. Внеш­ний угол при вер­ши­не B равен 146°. Най­ди­те угол C. Ответ дайте в градусах.

4.1. Прямая, параллельная стороне треугольника , пересекает стороны и в точках и соответственно. Найдите , если , .

4.2. В выпуклом четырёхугольнике ABCD углы BCA и BDA равны. Докажите, что углы ABD и ACD также равны.
Билет № 4

1. Треугольник: определение и виды. Равные треугольники (определение). Признаки равенства треугольников.

2. Трапеция: определение и виды. Вывод формулы площади трапеции.

3.1. Касательные в точках A и B к окружности с центром O пересекаются под углом 56°. Найдите угол ABO. Ответ дайте в градусах.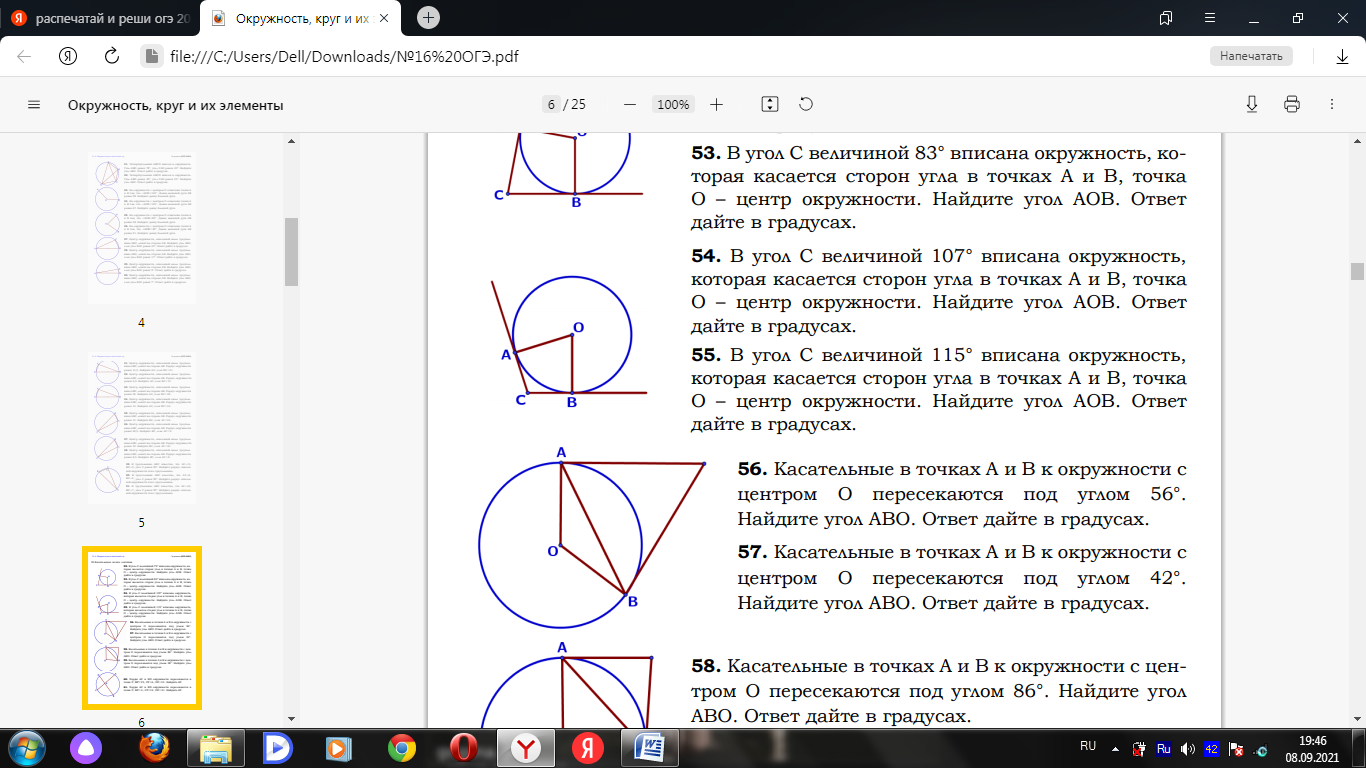



3.2. В треугольнике известно, что , . Найдите угол . Ответ дайте в градусах.

3.3. В тре­уголь­ни­ке     угол     равен 90°,   . Най­ди­те   .

4.1. Точка является основанием высоты, проведённой из вершины прямого угла треугольника к гипотенузе . Найдите , если , .

4.2. Докажите, что отрезок, соединяющий середины оснований трапеции, делит её на две равные по площади части.
Билет № 5

1. Параллелограмм: определение, свойства и признаки.

2. Теорема Фалеса (доказательство).

3.1. В равностороннем треугольнике АВС проведена высота BD. Найдите углы треугольника ABD.

3.2. Четырёхугольник ABCD вписан в окружность. Угол ABD равен 51°, угол CAD равен 42°.Найдите угол ABC. Ответ дайте в градусах.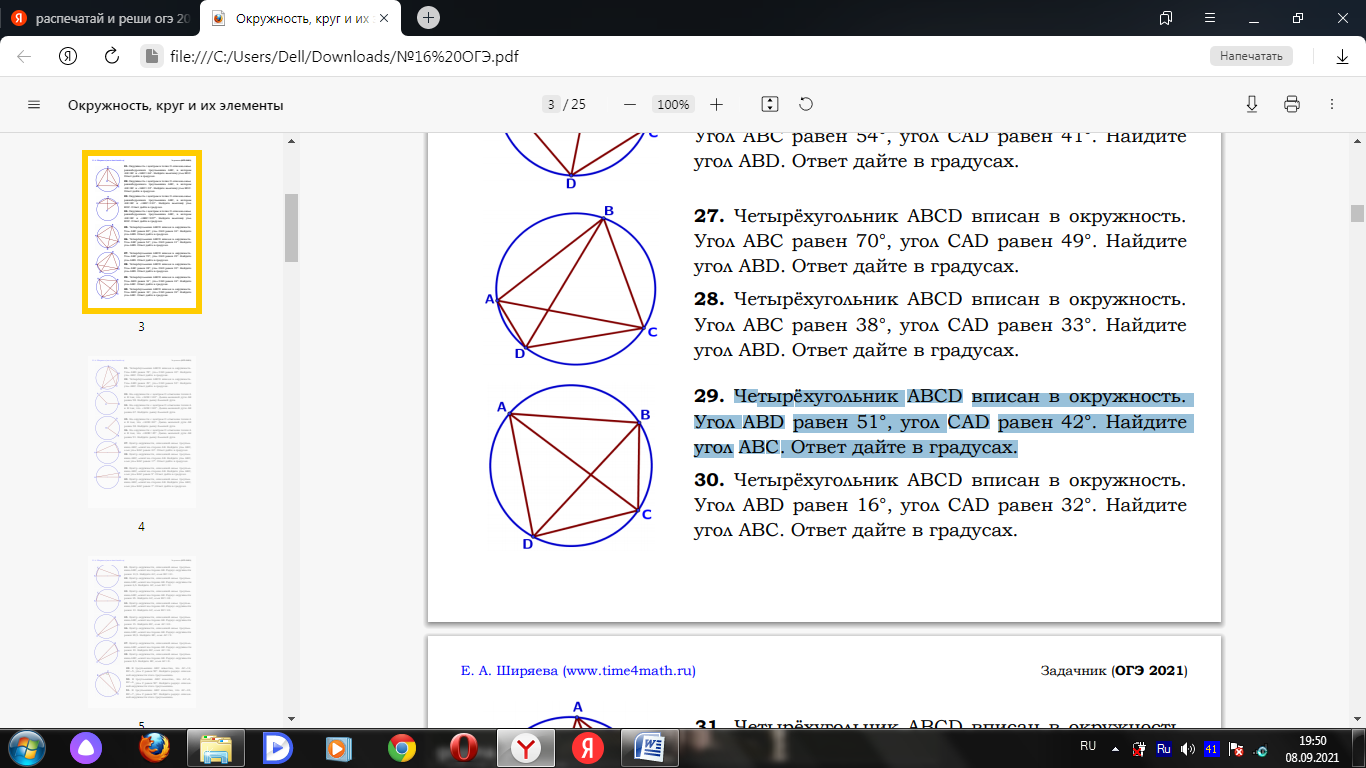



3.3. В пря­мо­уголь­ном тре­уголь­ни­ке катет , а вы­со­та , опу­щен­ная на гипотенузу, равна Най­ди­те .

4.1. Прямая, параллельная основаниям трапеции , пересекает еѐ боковые стороны и в точках и соответственно. Найдите длину отрезка , если , , .

4.2. Известно, что около четырёхугольника ABCD можно описать окружность и что продолжения сторон AB и CD четырёхугольника пересекаются в точке M . Докажите, что треугольники MBC и MDA подобны.

Билет № 6

1. Вектор. Длина (модуль) вектора. Координаты вектора. Равенство векторов.

2. Равнобедренный треугольник. Свойство медианы равнобедренного треугольника, проведенной к основанию (доказательство).

3.1. В остроугольном равнобедренном треугольнике угол между основанием и высотой, проведенной к боковой стороне, равен 34°. Найдите углы этого треугольника.

3.2. Один угол па­рал­ле­ло­грам­ма в два раза боль­ше другого. Най­ди­те мень­ший угол. Ответ дайте в градусах.

3.3. Найдите пло­щадь пря­мо­уголь­но­го треугольника, если его катет и ги­по­те­ну­за равны со­от­вет­ствен­но 12 и 13.

4.1. Найдите боковую сторону трапеции , если углы и равны соответственно и , а .

2. 
   Высоты AA₁ и BB₁ остроугольного треугольника ABC пересекаются в точке E . Докажите, что углы AA₁ B₁ и ABB₁ равны.
   

Билет № 7

1. Прямоугольник: определение и свойства.

2. Средняя линия треугольника. Теорема о средней линии треугольника (доказательство).

3.1. Найдите сторону ромба, если известно, что его диагонали равны 24 см и 32 см.

3.2. Разность углов, при­ле­жа­щих к одной сто­ро­не параллелограмма, равна 40°. Най­ди­те мень­ший угол параллелограмма. Ответ дайте в градусах.

3.3. В тре­уголь­ни­ке     угол     равен 90°,   . Най­ди­те   .

4.1. Биссектрисы углов и параллелограмма пересекаются в точке, лежащей на стороне . Найдите , если .

4.2. Точка E — середина боковой стороны AB трапеции ABCD . Докажите, что площадь треугольника ECD равна половине площади трапеции.
Билет № 8

1. Ромб: определение и признаки.

2. Треугольник: определение и виды. Теорема о сумме углов треугольника (доказательство).

3.1. На окружности с центром O отмечены точки A и B так, что AOB=80°. Длина меньшей дуги AB равна 58. Найдите длину большей дуги.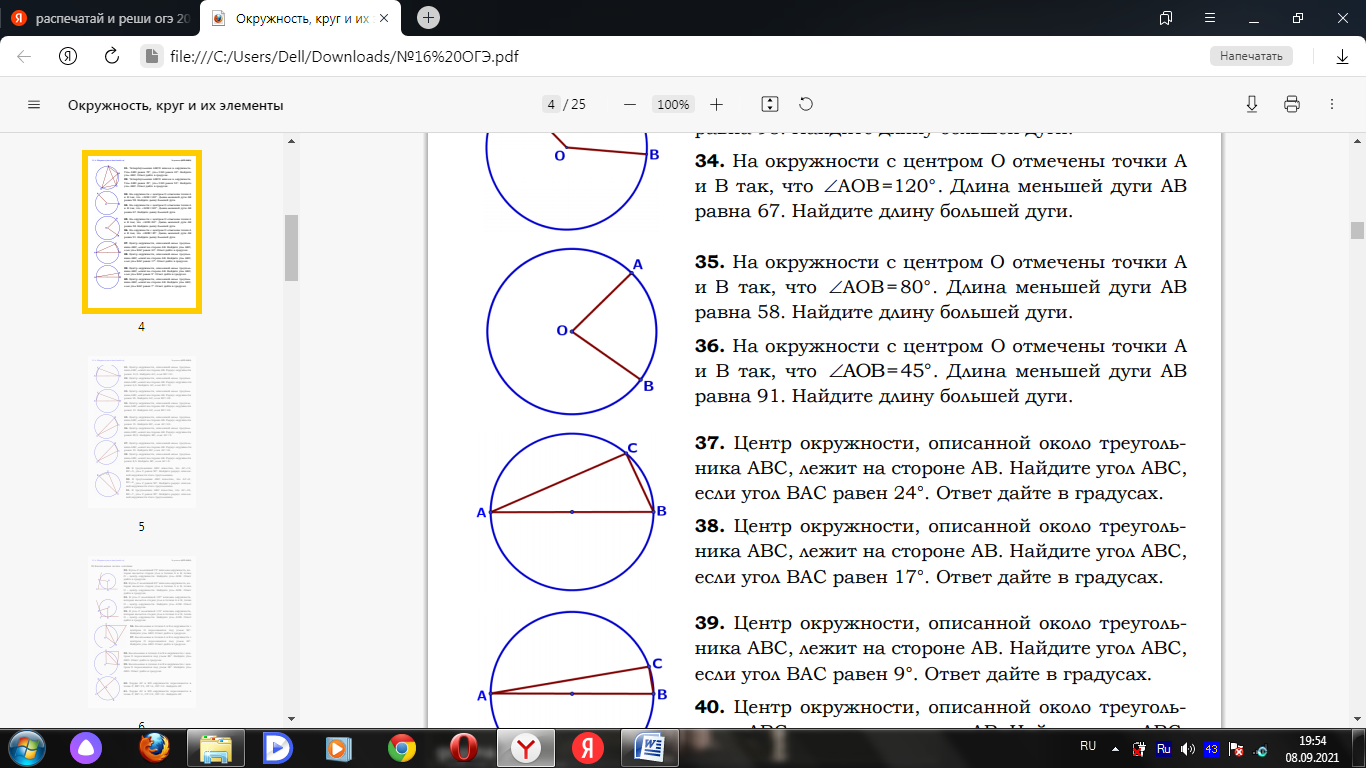



3.2. Катеты прямоугольного треугольника равны 8 и 15. Найдите гипотенузу этого треугольника.

3.3. Один из острых углов прямоугольного треугольника равен 23°. Найдите его другой острый угол. Ответ дайте в градусах.

4.1. Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 15, а одна из диагоналей ромба равна 60. Найдите углы ромба.

4.2. Биссектрисы углов и параллелограмма ABCD пересекаются в точке E стороны BC .Докажите,что E —середина BC .

Билет № 9

1. Внешний угол треугольника: определение и свойство.

2. Ромб. Свойства диагоналей ромба (доказательство одного из них по выбору учащегося).

3.1. Найдите число сторон выпуклого многоугольника, сумма внутренних углов которого равна 4320°.

3.2. В треугольнике известно, что , , угол равен 90°. Найдите радиус описанной окружности этого треугольника.

3.3. Сумма двух углов рав­но­бед­рен­ной тра­пе­ции равна 140°. Най­ди­те боль­ший угол трапеции. Ответ дайте в градусах.

4.1. Высота ромба делит сторону на отрезки и . Найдите высоту ромба.

4.2. В треугольнике ABC с тупым углом ACB проведены высоты AA₁ и BB₁ . Докажите, что треугольники A1CB1 и ACB подобны.
Билет № 10

1. Подобные треугольники (определение). Признаки подобия треугольников.

2. Теорема о сумме углов выпуклого n-угольника (доказательство).

3.1. Найдите медиану, проведенную к гипотенузе прямоугольного треугольника, если известно, что его катеты равны 8 см и 6 см.

3.2. Найдите мень­ший угол рав­но­бед­рен­ной трапеции, если два ее угла от­но­сят­ся как 1:2. Ответ дайте в градусах.

3.3. Хорды AC и BD окружности пересекаются в точке P, BP=15, CP =6, DP =10 . Найдите AP.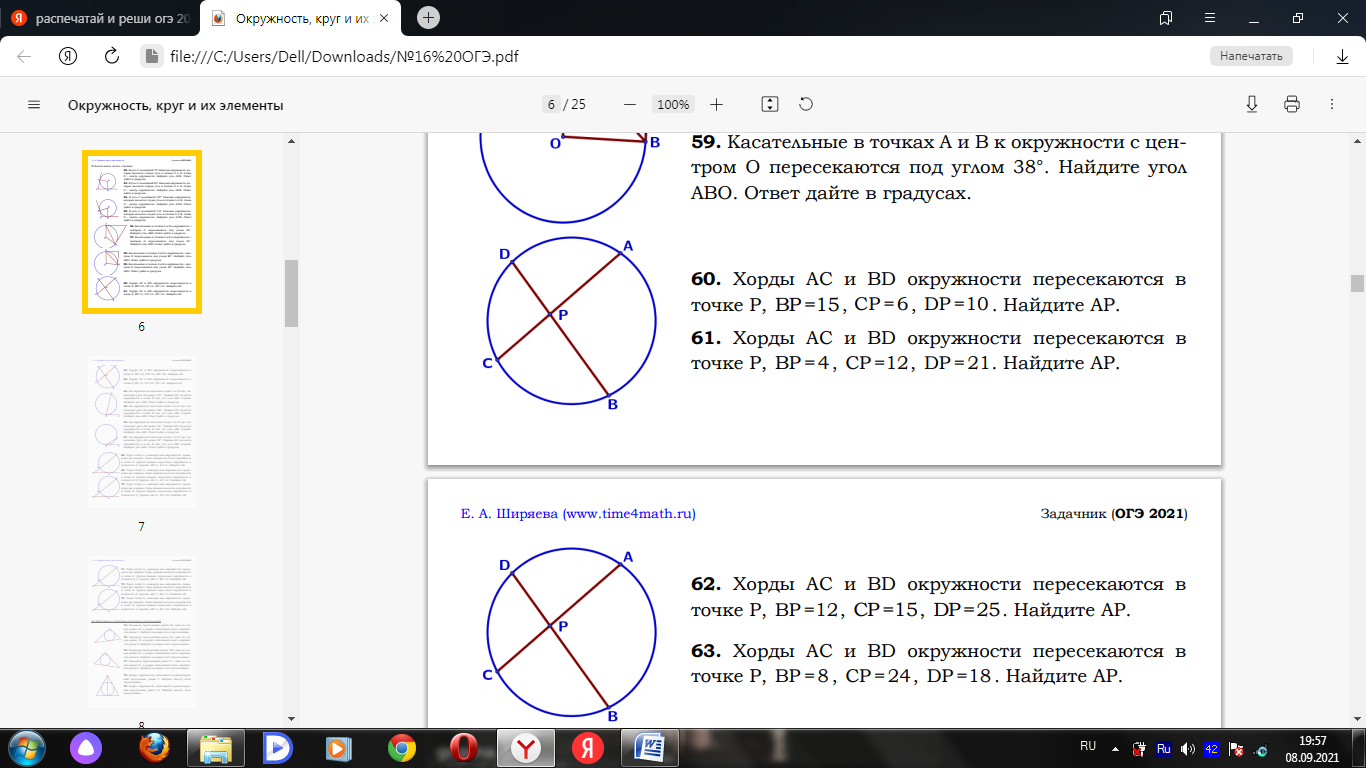



4.1. Биссектрисы углов и при боковой стороне трапеции пересекаются в точке . Найдите , если , .

4.2. В трапеции ABCD с основаниями AD и BC диагонали пересекаются в точке O . Докажите, что площади треугольников AOB и COD равны.

Билет № 11

1. Медиана, биссектриса и высота треугольника: определения и свойства.

2. Ромб. Вывод формулы площади ромба.

3.1. В прямоугольный треугольник вписана окружность радиуса 4 см. Найдите периметр этого треугольника, если известно, что его гипотенуза равна 26 см.

3.2. Основания тра­пе­ции равны 4 см и 10 см. Диа­го­наль трапеции делит сред­нюю линию на два отрезка. Най­ди­те длину боль­ше­го из них.

3.3.Площадь параллелограмма равна 54, а две его стороны равны 9 и 18. Найдите его высоты. В ответе укажите большую высоту.

4.1. Отрезки и являются хордами окружности. Найдите длину хорды , если , а расстояния от центра окружности до хорд и равны соответственно 12 и 5.

4.2. Докажите, что медиана треугольника делит его на два треугольника, площади которых равны между собой.
Билет № 12

1. Синус и косинус острого угла прямоугольного треугольника: определение, значения некоторых углов (30°, 45° и 60°).

2. Равнобедренный треугольник. Свойство углов при основании равнобедренного треугольника и признак равнобедренного треугольника (доказательство по выбору учащихся).

3.1. В треугольнике АВС угол С равен 90⁰, АС=15, cosА= . Найдите АВ.

3.2. Най­ди­те угол АDС рав­но­бед­рен­ной тра­пе­ции ABCD, если диа­го­наль АС об­ра­зу­ет с ос­но­ва­ни­ем ВС и бо­ко­вой сто­ро­ной АВ углы, рав­ные 30° и 40° со­от­вет­ствен­но.

3.3. Сторона AC тре­уголь­ни­ка ABC про­хо­дит через центр опи­сан­ной около него окружности. Най­ди­те ∠C , если ∠A = 44°. Ответ дайте в градусах.

4.1. Углы и треугольника равны соответственно и . Найдите , если радиус окружности, описанной около треугольника , равен 8.

4.2. Окружности с центрами в точках О₁ и О₂ пересекаются в точках A и B , причём точки О₁ и О₂ лежат по одну стороны от прямой AB . Докажите, что AB и О₁ О₂ перпендикулярны.
Билет № 13

1. Угол между векторами. Скалярное произведение векторов: определение и свойства.

2. Формулы площади треугольника. Вывод формулы площади треугольника через две стороны и угол между ними.

3.1. В остроугольном треугольнике ABC проведена высота BH, BAC=37°. Найдите угол ABH. Ответ дайте в градусах.

3.2. К окруж­но­сти с цен­тром в точке О про­ве­де­ны ка­са­тель­ная AB и се­ку­щая AO. Най­ди­те ра­ди­ус окружности, если AB = 12 см, AO = 13 см.

3.3. Най­ди­те пло­щадь ромба, если его диа­го­на­ли равны 14 и 6.

4.1. Вершины треугольника делят описанную около него окружность на три дуги, длины которых относятся, как 6:7:23. Найдите радиус окружности, если меньшая из сторон треугольника равна 12.

4.2. Биссектрисы углов B и C трапеции ABCD пересекаются в точке O , лежащей на стороне AD . Докажите, что точка O равноудалена от прямых AB , BC и CD .
Билет № 14

1. Тангенс острого угла прямоугольного треугольника: определение, значения некоторых углов (30°, 45° и 60°).

2. Центральный и вписанный углы. Свойство вписанного угла окружности(доказательство).

3.1. Точки A и B делят окруж­ность на две дуги, длины ко­то­рых относятся как 9:11. Най­ди­те величину цен­траль­но­го угла, опи­ра­ю­ще­го­ся на мень­шую из дуг. Ответ дайте в градусах.

3.2. Периметр ромба равен 40, а один из углов равен 30°. Най­ди­те пло­щадь ромба.

3.3. Точки M и N являются серединами сторон AB и BC треугольника ABC, сторона AB равна 26, сторона BC равна 39, сторона AC равна 48. Найдите MN.

4.1. Окружность, вписанная в треугольник , касается его сторон в точках , и . Найдите углы треугольника , если углы треугольника равны , и .

4.2. Через точку пересечения диагоналей параллелограмма ABCD проведена прямая,пересекающая стороны AB и CD в точках P и T соответственно.Докажите,что BP = DT .

Билет № 15

1. Окружность (определение). Центр, радиус, хорда, диаметр окружности. Взаимное расположение окружности и прямой. Касательная к окружности: определение и свойства.

2. Трапеция. Средняя линия трапеции. Свойство средней линии трапеции (доказательство).

3.1. В равностороннем треугольнике проведены две медианы. Найдите величину острого угла, образовавшегося при их пересечении.

3.2. Точка О — центр окруж­но­сти, ∠AOB = 118° (см. ри­су­нок). Най­ди­те ве­ли­чи­ну угла ACB (в гра­ду­сах).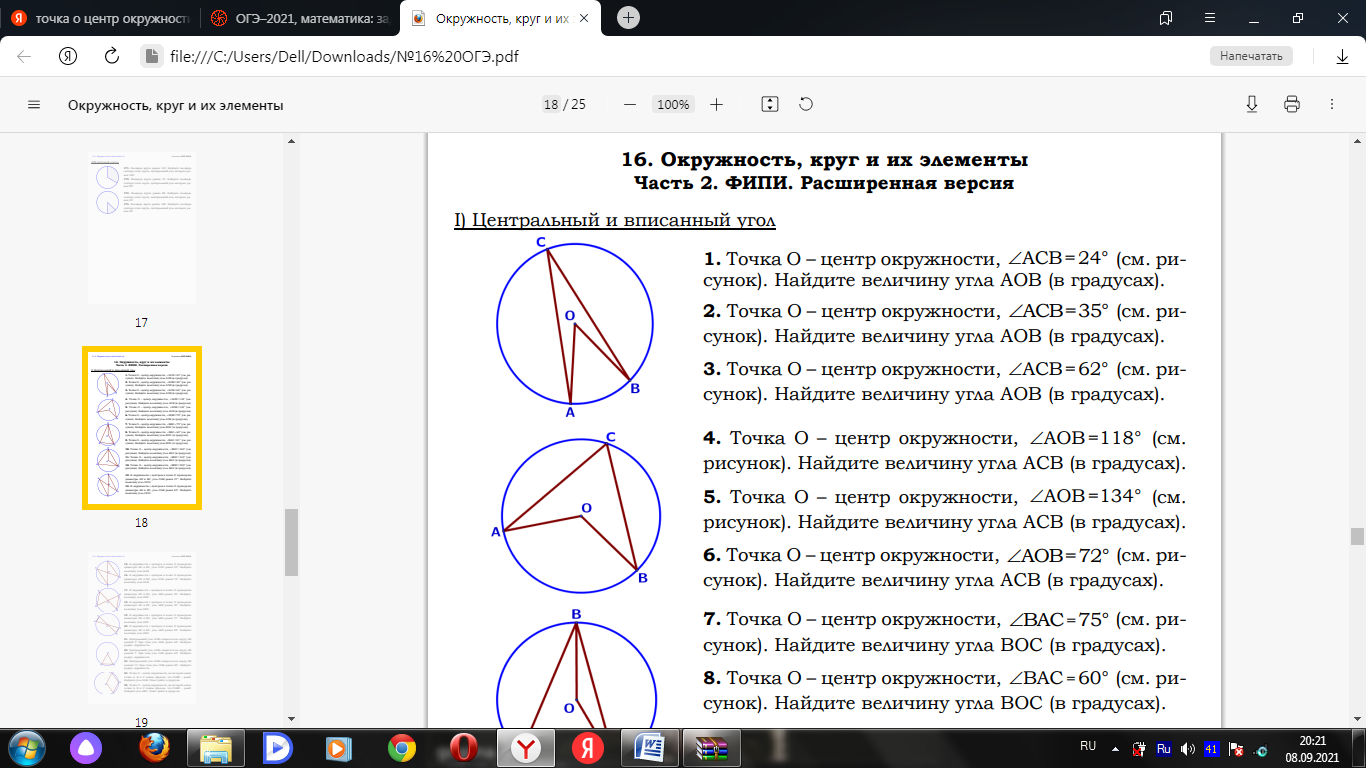



3.3. Диагональ прямоугольника образует угол 70° с одной из его сторон. Найдите острый угол между диагоналями этого прямоугольника. Ответ дайте в градусах.

4.1. Точка является основанием высоты , проведенной из вершины прямого угла прямоугольного треугольника . Окружность с диаметром пересекает стороны и в точках и соответственно. Найдите , если .

4.2. На сто­ро­не АС тре­уголь­ни­ка АВС вы­бра­ны точки D и E так, что от­рез­ки AD и CE равны. Оказалось, что от­рез­ки BD и BE тоже равны. Докажите, что тре­уголь­ник АВС — равнобедренный.