Задачи по физике. 1. в однородном магнитном поле с индукцией 2Тл движется протон. Траектория его движения представляет винтовую линию радиусом 10см. Кинетическая энергия протона 3,6МэВ. Определить шаг винтовой линии. Д ано Решение
 Скачать 145.51 Kb. Скачать 145.51 Kb.
|
|
1. В однородном магнитном поле с индукцией 2Тл движется протон. Траектория его движения представляет винтовую линию радиусом 10см. Кинетическая энергия протона 3,6МэВ. Определить шаг винтовой линии. Д  ано: Решение: ано: Решение: Рассмотрим Рис.1. Поскольку протон движется Рассмотрим Рис.1. Поскольку протон движется 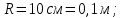 в магнитном поле по винтовой линии, то магнитное в магнитном поле по винтовой линии, то магнитное 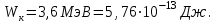 поле должно быть однородным, а протон в поле должно быть однородным, а протон в 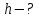 начальный момент времени влетает в это поле под острым углом начальный момент времени влетает в это поле под острым углом 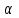 , с начальной скоростью , с начальной скоростью 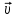 . Зададим систему отсчёта. За начало отсчёта принимаем точку 0, в которой протон влетает в магнитное поле, ось у направим по направлению вектора магнитной индукции . Зададим систему отсчёта. За начало отсчёта принимаем точку 0, в которой протон влетает в магнитное поле, ось у направим по направлению вектора магнитной индукции 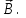 Ось z строим в плоскости, в которой лежат вектора Ось z строим в плоскости, в которой лежат вектора 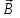 и и 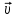 , перпендикулярно оси у. Ось х строим перпендикулярно осям у и z (Рис. 1.). , перпендикулярно оси у. Ось х строим перпендикулярно осям у и z (Рис. 1.).Начальную скорость протона 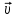 разложим по двум составляющим разложим по двум составляющим 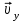 , и , и 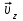 . Тогда проекции составляющих начальной скорости протона на оси координат будут: . Тогда проекции составляющих начальной скорости протона на оси координат будут: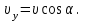 (1) (1)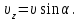 (2) (2)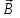 Протон двигается по спиральной линии. За счёт составляющей скорости 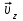 на протон в магнитном поле будет действовать сила Лоренца которая предаст ему нормального ускорения, а за счёт составляющей скорости на протон в магнитном поле будет действовать сила Лоренца которая предаст ему нормального ускорения, а за счёт составляющей скорости 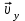 протон будет совершать равномерное движение по направлению оси у. Результирующее движение и будет движением по спиральной линии. протон будет совершать равномерное движение по направлению оси у. Результирующее движение и будет движением по спиральной линии.По второму закону Ньютона можно записать: 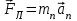 . (3) . (3)Учитывая, что модуль силы Лоренца равен: 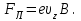 (4) (4)Модуль нормального ускорения вычисляется по формуле: 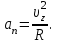 (5) (5)После подстановки (4) и (5) в (3), для проекций, получаем: 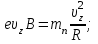 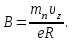 (6) (6)Где 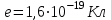 - заряд протона (модуль заряда электрона), - заряд протона (модуль заряда электрона), 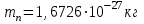 - масса покоя протон. - масса покоя протон.После подстановки (2) в (6), имеем: 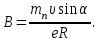 (7) (7)Кинетическая энергия протона вычисляется по формуле: 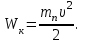 (8) (8)С формулы (8) найдём скорость протона, с которой он влетает в магнитное поле: 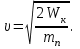 (9) (9)После подстановки (9) в формулу (7), получаем: 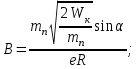 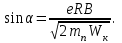 (10) (10)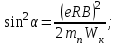 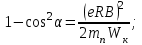 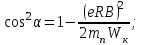 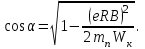 (11) (11)Учитывая, что скорость равномерного движения протона по окружности определяется по формуле: 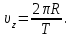 (12) (12)Находим период винтовой линии: 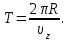 (13) (13)За время одного оборота (за период) протон по оси х сместится на расстояние шага винтовой линии, двигаясь в этом направлении равномерно прямолинейно. Вычисляем шаг винтовой линии h по формуле: 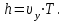 (14) (14)После подстановки (3) в формулу (14), получаем: 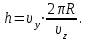 (15) (15)C учётом (1), (2) уравнение (15) принимает вид: 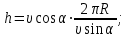 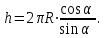 (16) (16)После подстановки (10) и (11) в формулу (16), получаем: 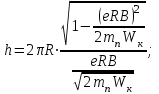 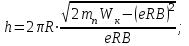 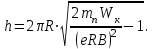 (17) (17)Подставим численные значения физических величин в расчётную формулу (17) и произведём вычисления: 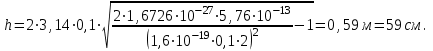 Ответ: 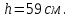 2. Плоский виток площадью 10см2 сделан из проволоки сопротивлением 0,5Ом. Силовые линии однородного магнитного поля с индукцией 4Тл перпендикулярны плоскости витка. К витку присоединен гальванометр. Найти электрический заряд, прошедший через гальванометр при повороте витка на угол 120°. Дано: Решение: 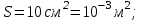 Рассмотрим рисунки 2 и 3. При медленном повороте витка Рассмотрим рисунки 2 и 3. При медленном повороте витка 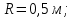 в магнитном поле индукционными токами можно в магнитном поле индукционными токами можно 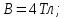 пренебречь и считать ток в контуре неизменным. Работа сил пренебречь и считать ток в контуре неизменным. Работа сил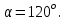 поля в этом случае определяется выражением: поля в этом случае определяется выражением: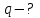 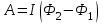 . (1) . (1)Где Ф1 и Ф2 - магнитные потоки, пронизывающие контур в начальном и конечном положениях, 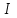 - ток в витке. - ток в витке.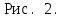 Работа внешних сил будет равна модулю работы сил поля и противоположна ей по знаку, то есть: 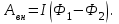 (1) (1)Так как в начальном положении контур установился свободно (положение устойчивого равновесия), то момент внешних сил, действующих на контур, равен нулю. В этом положении вектор магнитного момента 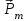 контура сонаправлен с вектором контура сонаправлен с вектором 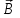 (Рис. 2) и магнитный поток Ф1 максимален (Рис. 2) и магнитный поток Ф1 максимален 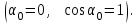 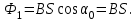 (2) (2)Где S – площадь контура, 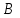 модуль вектора индукции магнитного поля. модуль вектора индукции магнитного поля.В конечном положении (Рис. 3.) вектор магнитного момента 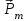 образует угол образует угол 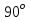 с вектором с вектором 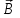 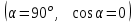 и магнитный поток: и магнитный поток: 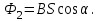 (3) (3)Перепишем выражение (1) с учетом (2) и (3): 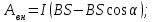 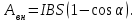 (4) (4)Работа внешних сил вычисляется по формуле: 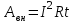 . (5) . (5)Где 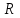 - сопротивление проволоки, из которой изготовлен виток, - сопротивление проволоки, из которой изготовлен виток, 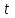 - время поворота витка на угол - время поворота витка на угол 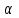 . .После подстановки (5) в формулу (4), получаем: 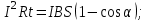 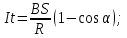 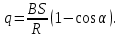 (6) (6)Где 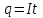 - заряд, который протекает через сечения провода витка за время поворота витка на угол - заряд, который протекает через сечения провода витка за время поворота витка на угол 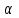 . .Подставим численные значения физических величин в расчётную формулу (6) и произведём вычисления: 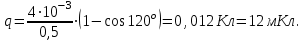 Ответ: 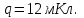 |
