геом 11 кл. 1 вариант Задания уровня а вам предложены тестовые задания. Каждое здание оценивается в 1 балл
 Скачать 113.87 Kb. Скачать 113.87 Kb.
|
|
1 вариант Задания уровня А Вам предложены тестовые задания. Каждое здание оценивается в 1 балл. Сколько плоскостей можно провести через три точки пространства не принадлежащие одной прямой. A)Ни одной B)Три C)Одну D)Бесконечно много Для правильной шестиугольной призмы АBCDEFA1B1C1D1E1F1 укажите ребро параллельное ребру B1C1 A)AA1 B) C1D1 C) EF D) DE Назовите общую прямую плоскостей РВМ и МАВ A) РМ; B) А В; C) РВ; D) ВМ. 1.4. Точка А отстоит от плоскости на расстоянии 18см. Найдите длину наклонной, проведенной из нее под углом 600 к этой плоскости. A) 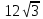 B) 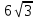 C) 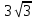 D) 8 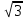 E) 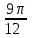 1.5. . Из точки В — вершины прямоугольника АВСD восстановлен перпендикуляр ВМ к плоскости прямоугольника. Найти МD, если CD=8, МС=15. A)17 см B) 12 см C) 13 см D) 20 см 1.6. Расстояние от точки D до каждой из вершин равностороннего треугольника АВС равно 4 см. АВ=6 см. Найдите расстояние от точки Д до плоскости АВС. A)2 см B) 4 см C) 3 см D) 6 см 1.7. Даны векторы 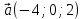 и и 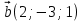 . Найти координаты вектора . Найти координаты вектора 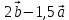 A) 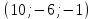 B) 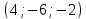 C) 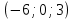 D) 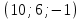 1.8. Дан куб АВСDА1В1С1D1  Найдите, какие из трех векторов будут компланарны друг другу А) 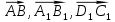 В) 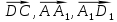 С) 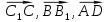 Задания уровня В 2.1. Ребро куба ABCDA1B1C1D1 равно 4 см. Через диагональ основания BD под углом 45° кплоскости основания проведена плоскость BDK, пересекающая боковое ребро в точке K.Найдите площадь треугольника BDK. [2] 2.2. Найдите угол между вектором 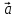 (5; -1; 7) и осью ОХ [3] (5; -1; 7) и осью ОХ [3]2.3. Напишите уравнение сферы с центром в начале координат, если плоскость х=5 касается этой сферы. Сфера задана уравнением х2 + y2 + z2 -2x + 4y - 6z - 2=0 . Найдите координаты центра сферы и ее радиус. [3] 2 вариант Задания уровня А Вам предложены тестовые задания. Каждое здание оценивается в 1 балл. 1.1. Сколько плоскостей можно провести через три точки пространства принадлежащие одной прямой. A)Ни одной B)Три C)Одну D)Бесконечно много 1.2. Для правильной шестиугольной пирамиды SАBCDEF укажите прямую, параллельную линии пересечения плоскостей SАB и SDE: A)BC B) CF C) AD D) BE 1.3 Назовите общую прямую плоскостей AFD и DEF. А) AF; В) FD; C) AE; D) ) ED. 1.4. Точка А отстоит от плоскости на расстоянии 12см. Найдите длину наклонной, проведенной из нее под углом 600 к этой плоскости. A) 8 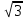 B) 4 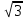 C) 2 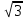 D) 6 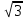 1.5. Из точки вне плоскости проведены к ней две наклонные, одна из которых равна 16 см и наклонена под углом 30° к плоскости. Определить длину второй наклонной, если ее проекция на плоскость равна 15 см. A)12 см B) 13см C) 10 см D) 17 см 1.6. Расстояние от точки D до каждой из вершин равностороннего треугольника АВС равно 5 см. АВ=3 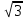 см. Найдите расстояние от точки М до плоскости АВС см. Найдите расстояние от точки М до плоскости АВС A) 4 см B) 3 см C) 5 см D) 2 см 1.7 Даны векторы 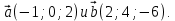 Найти координаты вектора Найти координаты вектора 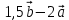 . . . . A) 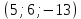 B) 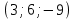 C) 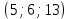 D) 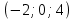 1.8. Дан куб АВСDА1В1С1D1  Найдите, какие из трех векторов будут компланарны друг другу А) 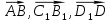 В) 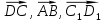 С) 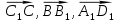 Задания уровня В 2.1.Ребро куба ABCDA1B1C1D1 равно 6 см. Через диагональ основания BD под углом 45° к плоскости основания проведена плоскость BDK, пересекающая боковое ребро в точке K. Найдите площадь треугольника BDK. [2] 2.2. Найдите угол между вектором 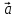 (4; -3; 5) и осью ОY. [3] (4; -3; 5) и осью ОY. [3] 2.3 а) Напишите уравнение сферы с центром в начале координат, если плоскость х=6 касается этой сферы. б) Сфера задана уравнением х2 + y2 + z2 -4x + 2y - 6z - 2=0 . Найдите координаты центра сферы и ее радиус. |
