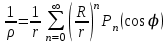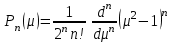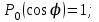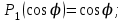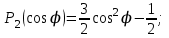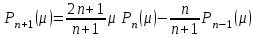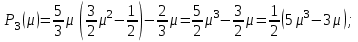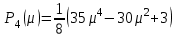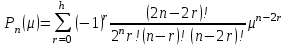1 Вычисление длин дуг меридианов и параллелей
 Скачать 0.6 Mb. Скачать 0.6 Mb.
|
Задание № 4. Вычисление нормального потенциала силы тяжестиЗадание Рассчитать нормальный потенциал силы тяжести для эллипсоида №1 в приложении (Таблица 2) для n=2, 4, 6, 8
где – а – большая полуось эллипсоида № 1 из таблицы № 1 приложения, 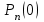 - полиномы Лежандра степени n и порядка m=0 для - полиномы Лежандра степени n и порядка m=0 для 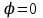 ; ; 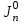 - коэффициенты зональных гармоник. - коэффициенты зональных гармоник.Гармонические коэффициенты 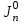 вычисляются по значениям фундаментальных геодезических постоянных вычисляются по значениям фундаментальных геодезических постоянных 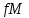 , , 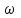 , , 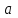 , , 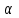 . Значения . Значения 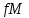 , , 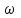 взять из ПЗ 90.11, взять из ПЗ 90.11, 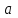 , , 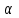 посчитать по параметрам эллипсоида № 1. посчитать по параметрам эллипсоида № 1.Фундаментальные геодезические постоянные имеют следующие значения:  Вычисляем: 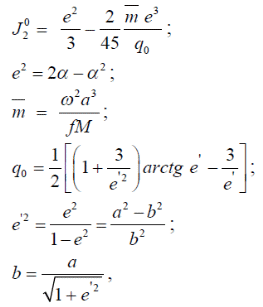 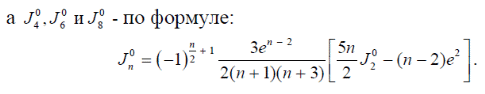 Определим выражения для сферических функций при различных значениях 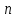 как функцию как функцию 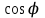 . Из (16) . Из (16)
следует, что
и т.д. Обозначим 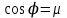 . .Последующие функции найдем, используя следующее свойство сферических функций. Три последовательных многочлена Лежандра (сферические функции первого рода) связаны рекуррентной формулой
Тогда, для 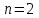 найдем найдем 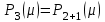 , т.е. , т.е.
и т.д. Для реализации на ЭВМ имеется другая формула вычислений 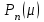 . .
где 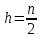 при при 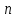 - четном, - четном, 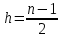 при при 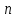 - нечетном. - нечетном.Из формулы (17) следует, что многочлены 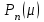 с четными индексами с четными индексами 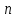 содержат только четные степени содержат только четные степени 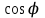 , а с нечетными , а с нечетными 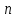 - нечетные степени - нечетные степени 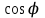 . . |

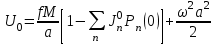 .
.