1 Вычисление длин дуг меридианов и параллелей
 Скачать 0.6 Mb. Скачать 0.6 Mb.
|
|
Таблица № 2 Номенклатура карт масштаба 1:100000 в листе масштаба 1:1000000
Таблица № 3 Номенклатура трапеций масштаба 1:1000000.
Задание № 2: Вычисление прямого и обратного азимута и длины дуги, соединяющей две точки 1. Использовать трапецию масштаба 1:100 000 в соответствии с заданием № 1. 2. Вычислить координаты средней точки для трапеции:
3. С помощью угловых и средней точек трапеции получить четыре треугольника:  Рис. 1 Треугольники, образующие трапецию 4. Вычислить прямые азимуты с точки P на все точки и обратные - со всех точек на точку P. Результат представить в таблице.
Вычисление азимутов и расстояний выполнять по следующим формулам и в следующей последовательности:
где - - 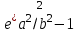 -квадрат второго эксцентриситета; -квадрат второго эксцентриситета; 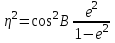 . .Обозначив правые части правых двух равенств через Q и P, получим:
Решение задачи завершается применением формул:
Длина линии определяется с погрешностью менее 0,5 м, если 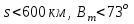 . С уменьшением расстояния в n раз погрешность вычисленного расстояния уменьшается в . С уменьшением расстояния в n раз погрешность вычисленного расстояния уменьшается в 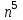 раз. раз.Задание № 3: Вычисление площадей и рамок съемочных трапеций Определить площадь трапеции каждой номенклатуры масштабного ряда: 1:100 000, 1:50 000, 1:25 000, 1:10 000 до 1:1000. Номер трапеции масштаба 1:100000 выбирают в соответствии с заданием 1, в остальных масштабных рядах для вычислений используют верхний левый лист. Сфероидической трапецией называется часть поверхности эллипсоида, ограниченная меридианами и параллелями. 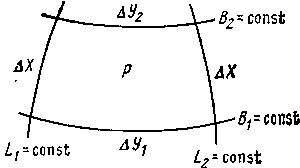 Площадь dP бесконечно малой сфероидической трапеции ABCD (рис.) на эллипсоиде, стороны которой являются элементами дуг меридианов и параллелей: 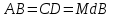 , , 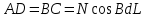 определяется как: определяется как:
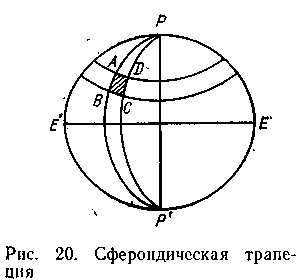 Рис. Сфероидическая трапеция Учитывая, что 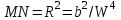 , ,где 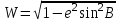 ; ; получим
Площадь конечной трапеции, ограниченной широтами В1 и B2 и долготами L1 и L2 (выраженными в секундах), выражается как:
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

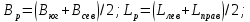 .
.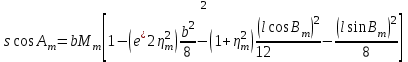 ;
;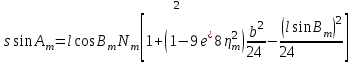 ;
;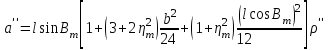 ;
;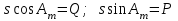 .
.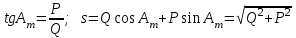 .
.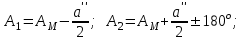 .
.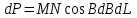 .
.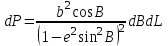 .
.