Отчет. 1. Вычислить определенный интеграл по формуле НьютонаЛейбница, предварительно вычислив первообразную

• Название: 1. Вычислить определенный интеграл по формуле НьютонаЛейбница, предварительно вычислив первообразную
• Дата: 13.05.2023
• Размер: 76.34 Kb.
• Имя файла: Отчет.docx
• Тип: Документы; #1126894

1. Вычислить определенный интеграл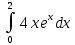



по формуле Ньютона-Лейбница, предварительно вычислив первообразную.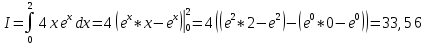



2. Вычислить определенный интеграл методом левых и правых прямоугольников. Построить график показывающий левые и

правые прямоугольники.

Код программы:

Метод левых прямоугольников:

a=0; b=2;

n=10

h=(b-a)/n;

x=a:h:b;

I1=0

for i=2:n

I1=I1+h*4*x(i)*exp(x(i))

end

I=4*(exp(b)*b-exp(b) - exp(a)*a+exp(a))

for i=1:n-1

z=h*4*x(i)*exp(x(i))

plot([x(i) x(i) x(i+1) x(i+1)],[0 z z 0])

end

plot([x(1) 0],[x(n) 0],'g')

Метод правых прямоугольников:

a=0; b=2;

n=100

h=(b-a)/n;

x=a:h:b;

I1=0

for i=1:n-1

I1=I1+h*4*x(i)*exp(x(i))

end

I=4*(exp(b)*b-exp(b) - exp(a)*a+exp(a))

for i=1:n-1

z=h*4*x(i)*exp(x(i))

plot([x(i) x(i) x(i+1) x(i+1)],[0 z z 0])

end

plot([x(1) 0],[x(n) 0],'g')
Результат программы:

Метод левых прямоугольников: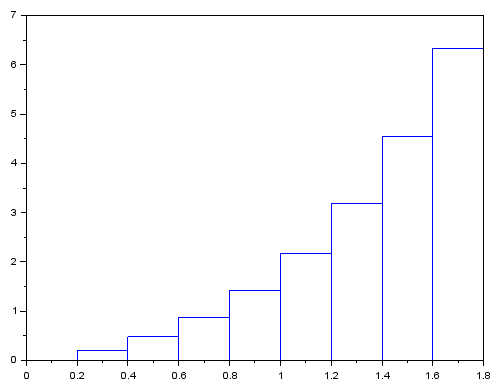





Метод правых прямоугольников: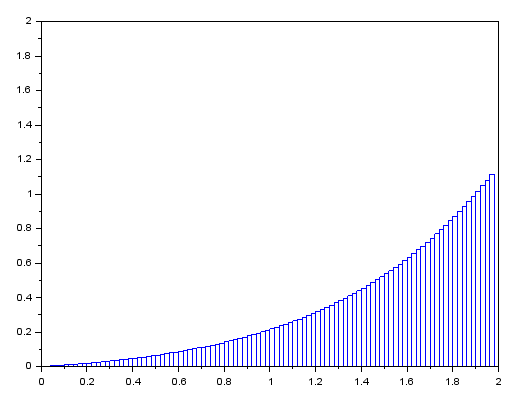





3. Вычислить определенный интеграл методом трапеций.

Код программы:

a=0; b=2;

n=40

h=(b-a)/n;

x=a:h:b;

I1=0

for i=1:n-1

I1=I1+h*(4*x(i)*exp(x(i))+4*x(i+1)*exp(x(i+1)))/2

end

I=4*(exp(b)*b-exp(b) - exp(a)*a+exp(a))

for i=1:n

z=h*4*x(i)*exp(x(i))

z1=h*4*x(i+1)*exp(x(i+1))

plot([x(i) x(i) x(i+1) x(i+1) ],[0 z z1 0 ])

end

plot([x(1) 0],[x(n) 0],'g')

Результат программы: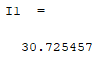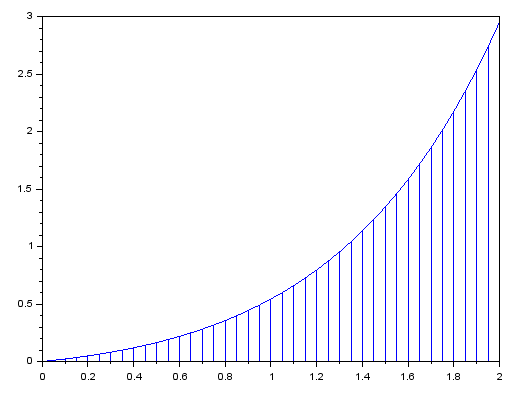





4. Вычислить определенный интеграл с помощью функции linspline.

Код программы:

a=0; b=2;

n=10;

h=(b-a)/n;

x=a:h:b;

intsplin(x,4*x.*exp(x))

Результат программы: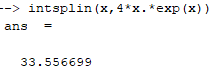



5. Вычислить определенный интеграл с помощью функции integrate.

Код программы:

a=0; b=2;

n=10;

h=(b-a)/n;

x0=a;x1=a:h:b;

X=integrate('4*x.*exp(x)','x',x0,x1);

X

Результат программы: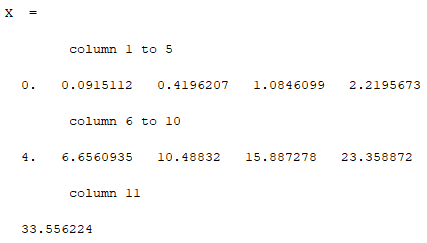



6. Вычислить определенный интеграл с помощью функции intg.

Код программы:

a=0; b=2;

function y=f(x)

y=4*x*exp(x);

endfunction

exact=33.556224;

I=intg(a,b,f)

abs(exact-I)

Результат программы: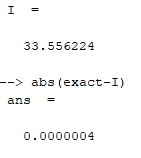



7. Построить графикb функции, определяемой по формуле 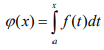, где f (t)‐ подынтегральная функция взятая по варианту. Графики для соответствующих функций вывести в одном окне и отдельно в двух подокнах.

Код программы:

С графиками в одном окне:

a=0;

b=2;

n=100;

h=(b-a)/n;

x=a:h:b;

y=4*x.*exp(x);

I1=inttrap(x,y)

I2=4*(exp(b)*b-exp(b) - exp(a)*a+exp(a))

I3=integrate('4*x.*exp(x)','x',a,b)

deff('y=f(x)','y=4*x.*exp(x)')

I4=intg(a,b,f)

I5=intsplin(x,y)

f4=[0];

x4=[a];

for x=a+h:h:b

x1=a:h:x;

y1=f(x1);

Itr=inttrap(x1,y1);

x4=[x4 x];

f4=[f4 Itr];

end

plot(x4,f4)

xgrid()

f5=[];

x5=[];

for x=a:h:b

I=intg(a,x,f);

x5=[x5 x];

f5=[f5 I];

end

plot(x5,f5)

xgrid()

С графиками отдельно в двух подокнах:

a=0;

b=2;

n=100;

h=(b-a)/n;

x=a:h:b;

y=4*x.*exp(x);

I1=inttrap(x,y)

I2=4*(exp(b)*b-exp(b) - exp(a)*a+exp(a))

I3=integrate('4*x.*exp(x)','x',a,b)

deff('y=f(x)','y=4*x.*exp(x)')

I4=intg(a,b,f)

I5=intsplin(x,y)

f4=[0];

x4=[a];

for x=a+h:h:b

x1=a:h:x;

y1=f(x1);

Itr=inttrap(x1,y1);

x4=[x4 x];

f4=[f4 Itr];

end

subplot(221)

plot2d(x4,f4)

xgrid()

f5=[];

x5=[];

for x=a:h:b

I=intg(a,x,f);

x5=[x5 x];

f5=[f5 I];

end

subplot(222)

plot2d(x5,f5)

xgrid()

Результат программы:

С графиками в одном окне: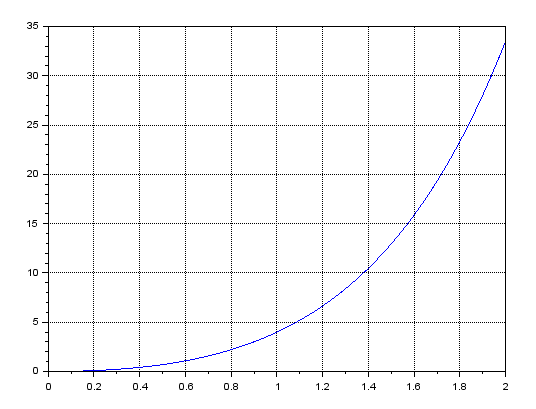



С графиками отдельно в двух подокнах: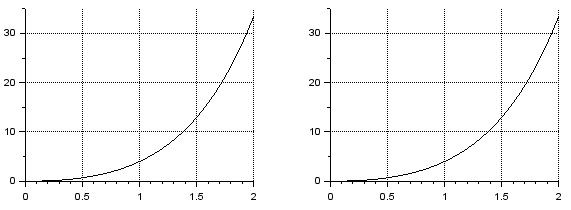