2 задачи 4 вар. 1. Вычислить zпреобразование дискретной последовательности отсчетов сигнала x(n), согласно своему
 Скачать 255.15 Kb. Скачать 255.15 Kb.
|
задачА 11. Вычислить Z-преобразование дискретной последовательности отсчетов сигнала {x(n)}, согласно своему варианту. 2. Определить дискретную свертку {y(n)}, если импульсная характеристика системы имеет вид (см. таблицу 1.1). Определить системную функцию H(Z). 3. Построить схему нерекурсивного фильтра, которому соответствует системная (передаточная) функция H(Z) и позволяющего получить рассчитанные выходные отсчеты {y(n)}. 4. По заданному Z-преобразованию X(Z) определить отсчеты дискретного сигнала {x(n)}, согласно своему варианту. Исходные данные приведены в таблице 1.1. Исходные данные Var 4 x = {0, 1, 0, 0, 1, 1, 1, 0} h = {2, 2, 2, 1, 1, 1, 1} 1.2 Выполнение задания 11.2.1 Z-преобразование дискретной последовательности отсчетов сигнала {x(n)}Дана дискретная последовательность отсчетов сигнала: {x(n)}= {0, 1, 0, 0, 1, 1, 1, 0} Прямое одностороннее Z-преобразование имеет вид: 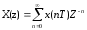 Подставив значения, получим: дискретный сигнал свертка фильтр 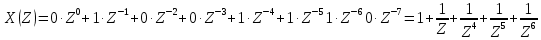 1.2.2 Определение дискретной свертки{x(n)}= {0, 1, 0, 0, 1, 1, 1, 0}, {h(m)}= {2, 2, 2, 1, 1, 1, 1} Сигнал на выходе дискретной цепи связан с сигналом на входе цепи формулой дискретной свертки, поэтому n-ый отсчет дискретной выходной последовательности рассчитывается как:  где 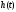 – импульсная характеристика цепи. – импульсная характеристика цепи.
 Определить системную функцию H(Z). C другой стороны, передаточной (системной) функцией дискретной цепи   1.2.3 Схема нерекурсивного фильтраКИХ-фильтры реализуются на основе свертки двух функций. Первая функция является входным сигналом 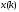 , а вторая , а вторая 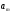 называется ядром фильтра и определяет его импульсную характеристику называется ядром фильтра и определяет его импульсную характеристику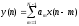 . .  (1.1) (1.1)Структурная схема (прямая структура), реализующая алгоритм (1.1) приведена на рисунке 1.4. Её транспонированная реализация приведена на рисунке 1.5 Алгоритм (1.1) можно представить в виде 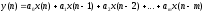 (1.2) (1.2)где – а0, а1, …аm действительные постоянные («весовые») коэффициенты; m – порядок нерекурсивного фильтра, т. е. максимальное число запоминаемых чисел. Формулы (1.1) и (1.2) тождественны, а коэффициенты а0, а1, …аm совпадают с соответствующими отсчетами импульсной характеристики фильтра h0, h1, …, hm. 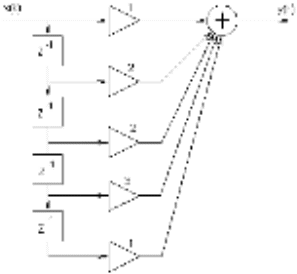 Рисунок 1 - Прямая структурная схема нерекурсивного фильтра 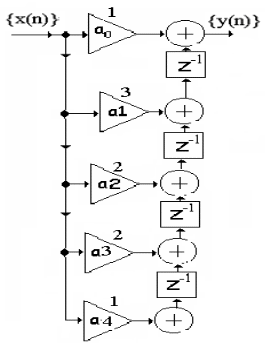 Рисунок 2 - Транспонированная структурная схема нерекурсивного фильтра По заданному Z-преобразованию X(Z) определить отсчеты дискретного сигнала {x(n)}. ЗАДАЧА 2. 1. Определить передаточную характеристику передаточную (системную) функцию рекурсивного ЦФ. Коэффициенты числителя « 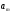 » и знаменателя « » и знаменателя «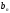 » определяются согласно своему варианту. » определяются согласно своему варианту.2. Разработать структурную схему рекурсивного фильтра, реализующую полученную передаточную функцию (прямую, каноническую и транспонированную реализации). 3. Рассчитать первые три отсчета импульсной характеристики фильтра {h(n)}, полученные при прохождении через разработанный фильтр сигнала {x(n)}={1,0,0}. Таблица 2.1 – Исходные данные Var 4 a0=2, a1=3, a2=2, a3=1, a4=1, a5=1, a6=1 b1=2, b2=2, b3=1, b4=1, b5=1 2.2 Выполнение задания 22.2.1 Передаточная характеристика рекурсивного ЦФАлгоритм цифровой фильтрации рекурсивного ЦФ имеет вид: 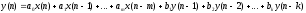 (2.1) (2.1)где bi и aj – вещественные коэффициенты. Или используя (4.13) [2]: 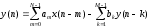 (2.2) (2.2)Перегруппировав входные и выходные отсчеты по разные стороны знака равенства, получим традиционную форму записи разностного уравнения: 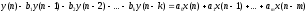 (2.3) (2.3)Применив Z-преобразование к (2.2; 2.3) и решив его относительно 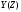 , найдем передаточную (системную) функцию рекурсивного ЦФ (5.6)[2]: , найдем передаточную (системную) функцию рекурсивного ЦФ (5.6)[2]: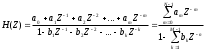 (2.4) (2.4)H (Z) =  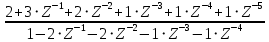 2.2.2 Структурные схемы рекурсивного фильтраПрямая форма рекурсивных фильтров реализуется непосредственно по его разностному уравнению (2.2) или по передаточной функции (7.2). Она содержит один сумматор, умножители и N+M-2=10 элемента задержки. Порядок фильтра равен пяти (см. рисунок 2.1). Недостаток такого способа реализации – сравнительно большое число ячеек памяти, уменьшить количество которых позволяет каноническая форма (см. рисунок 2.2). 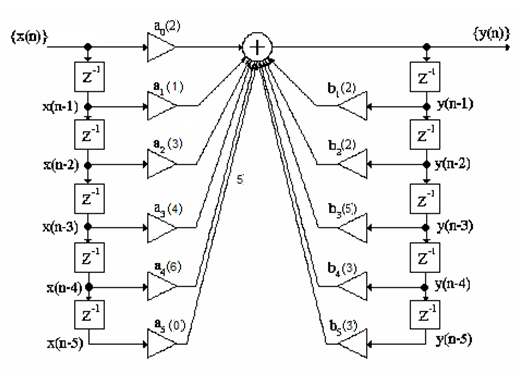 Рисунок 2.1 – Прямая структура рекурсивного фильтра 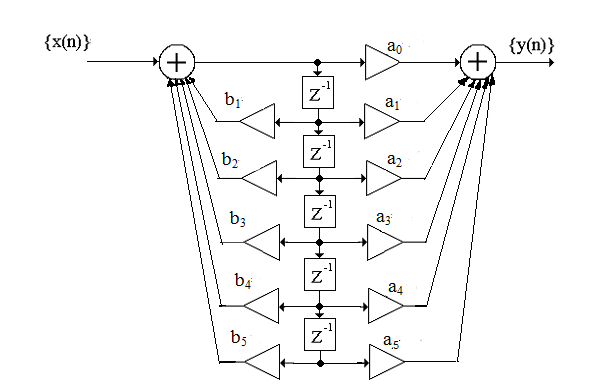 Рисунок 2.2 – Прямая каноническая структура рекурсивного фильтра Транспонированная структура представлена на рисунке 2.3. 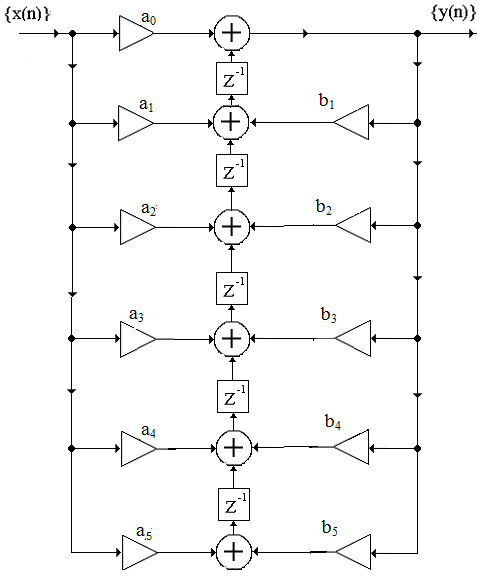 Рисунок 2.3 – Транспонированная структура рекурсивного фильтра 2.2.3 Отсчеты импульсной характеристики  (k): 2,9,44 |
