1. Виды и формы связей, различаемые в статистике
 Скачать 253.71 Kb.
|
|
1. Виды и формы связей, различаемые в статистике Различают два типа взаимосвязей между различными явлениями и их признаками: функциональную или жестко детерминированную и статистическую или стохастически детерминированную. Функциональная жестко детерминированная связь – это вид причинной зависимости, при которой определенному значению факторного признака соответствует одно или несколько точно заданных значений результативного признака. Этот вид связи встречается чаще в естественных науках, но также и в экономике. Стохастическая связь – это вид причинной зависимости, проявляющейся не каждом отдельном случае, а в общем, среднем, при большом числе наблюдений. Среди взаимосвязанных признаков одни могут рассматриваться как определенные факторы, влияющие на изменение других, а вторые как следствие, результат влияния первых. Корреляционная связь - частный случай стохастической связи, состоящей в том, что c изменением факторного признака (х) закономерным образом изменяется среднее значениерезультативного признака (y), в то время как в каждом отдельном случае y может принимать множество различных значений. Корреляционная связь между признаками может возникать различными путями. Важнейший путь – взаимосвязь вариации результативного признака с вариацией факторного признака. По направлению выделяют связь прямую и обратную (положительную и отрицательную), По аналитическому выражению линейную и нелинейную. Изучение корреляционных связей сводится в основном к решению следующих задач: выявление наличия (или отсутствия) связи между изучаемыми признаками; измерение степени тесноты связи между признаками; нахождение аналитического выражения связи, отражающей зависимость между х и у; экономическая интерпретация и практическое использование полученного результата. В начальной стадии анализа статистических зависимостей применяются простейшие методы оценки наличия связи, её направления и характера, выявляется форма воздействия одних факторов на другие. Для этих целей применяются методы приведения параллельных данных; графический и аналитических группировок. Метод приведения параллельных данных основан на сопоставлении двух или нескольких рядов статистических величин. Такое сопоставление позволяет установить наличие связи и получить представление о её характере. Графический метод используется для наглядного изображения формы связи между изучаемыми признаками. Для этого в прямоугольных осях координат строят график, по оси y, которого откладывают индивидуальные значения результативного признака, а по оси х – индивидуальные значения – факторного. Полученная совокупность точек называется полем корреляции. Метод аналитических группировок - исследуется связь между двумя и более признаками, из которых один рассматривается как результат, другой (другие) как фактор (факторы). Для установления связи между признаками данные группируются по признаку-фактору, который располагается в подлежащем аналитической таблицы. Изменения факторного признака при переходе от одной группы к другой вызывают соответствующие изменения результативного признака. Индекс Фехнера изменяется от [-1;1], при значении равном 1 он указывает на полную прямую связь, при значении –1 на полную обратную связь, при i=0 связь отсутствует. Промежуточные значения i характеризуют степень близости связи к функциональной. 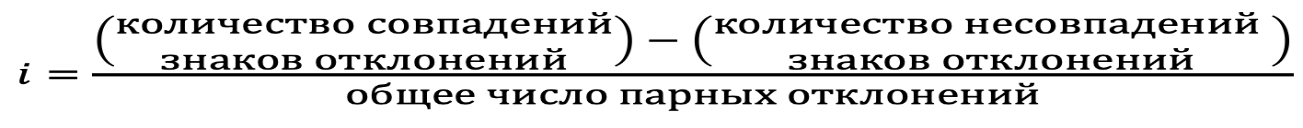 Самый известный измеритель тесноты связи между признаками - линейный коэффициент корреляции Пирсона (назван по имени английского статистика К. Пирсона, введшего это коэффициент в научный анализ), он характеризует тесноту и направление связи между двумя коррелируемыми признаками в случае наличия между ними линейной зависимости. 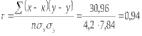 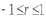 Полученное значение называется коэффициентом ковариации. Это – мера совместной вариации признаков. Или мы можем сказать, что это – мера соответствия вариации результативного признака вариации факторного. 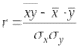 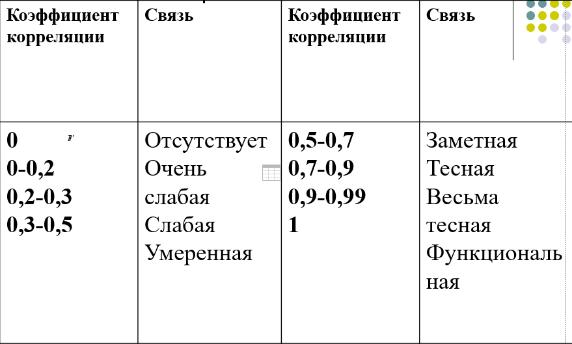 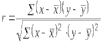 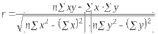 Коэффициент линейной корреляции, исчисленный по выборочным данным, является случайной величиной. Полученный из выборки коэффициент корреляции r является оценкой коэффициента корреляции в генеральной совокупности. С уменьшением числа наблюдений надежность коэффициента корреляции падает. Оценка существенности (значимости) линейного коэффициента корреляции основана на сопоставлении значения r с его средней квадратической ошибкой: 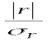 При оценке значимости коэффициента корреляции обычно рассматриваются следующие ситуации.Если число наблюдений достаточно велико (обычно свыше 30), а значение коэффициента корреляции не превышает 0.9, распределение коэффициента корреляции r можно считать приближенно нормальным со средней квадратической ошибкой: 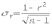 При достаточно большом числе наблюдений r должен превышать свою среднюю ошибку не менее, чем в три раза, если это неравенство не выполняется, то существование связи между признаками нельзя считать доказанным. Задавшись определенной вероятностью, можно построить доверительные границы r 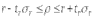 Для малого объема выборки, с распределением r далеким от нормального, применяются другие методы оценки значимости коэффициента корреляции. При небольшом числе наблюдений (n <30), средняя ошибка линейного коэффициента корреляции находится по формуле: 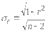 При этом выдвигается гипотеза о равенстве коэффициента корреляции нулю, то есть об отсутствии связи между y и x в генеральной совокупности. Для этого используется статистика: 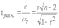 При малом числе наблюдений в выборке и высоком коэффициенте корреляции (распределение r отличается от нормального) для проверки гипотезы о наличии корреляционной связи, а также построения доверительного интервала применяется z-преобразование Фишера. Для этого рассчитывается величина  Распределение z приближается к нормальному. Вариация z выражается формулой: 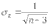 Ранговая корреляция. Если n вариантов ряда расположены в соответствии с возрастанием или убыванием признака х, то говорят, что объекты ранжированы по этому признаку. Ранг для хiуказывает место, которое занимает i-е значение признака среди других n значений признака х (i=1, 2, n). Коэффициент Спирмена 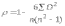 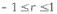 Значимость коэффициента Спирмена проверяется на основе t критерия Стьюдента по формуле: 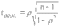 Коэффициент корреляции рангов (при условии, что ранги не повторяются) может быть рассчитан и по формуле, предложенной английским статистиком М. Кендаллом: 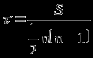 где S − фактическая разность рангов;  − максимальная сумма рангов.Этот коэффициент изменяется в интервале от [-1;1] и интерпретируется так же, как и коэффициент Пирсона, но дает более строгую оценку связи, чем коэффициент Спирмена, причем  . Это соотношение выполняется при большом числе наблюдений и слабых, либо умеренно тесных связях.При расчете коэффициента Кендалла соблюдается следующая последовательность действий: -Значения ранжируются в порядке возрастания или убывания. -Значения располагаются в порядке, соответствующем значениям -Для каждого ранга определяется число следующих за ним значений рангов, превышающих его величину. Результат записывается в столбец «+», суммируется и обозначается Р. -Определяется общая сумма S=P+Q. Значимость коэффициента корреляции рангов Кендалла проверяется по формуле  где tα- коэффициент, определяемый по таблице нормального распределения для выбранного уровня значимости α при больших n. Альтернативные признаки – это признаки, принимающие только два возможных значения. Исследования их корреляции основано на показателях, построенных на четырехклеточных таблицах, в которые сводятся значения признаков. 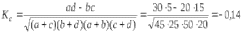 Коэффициент взаимной сопряженности К.Пирсона Для оценки тесноты связи между признаками, принимающими любое число вариантов значений (категориальные, номинальные признаки), применяется коэффициент взаимной сопряженности К.Пирсона. Основой изучения связи между номинальными признаками служит таблица сопряженности – двумерное распределение единиц совокупности по признакам. В этой таблице в измерении связи участвуют не значения признаков. Вся информация о наличии или отсутствии связи содержится в частотах появления сочетаний признаков. Коэффициент взаимной сопряженности определяется по формуле: 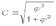 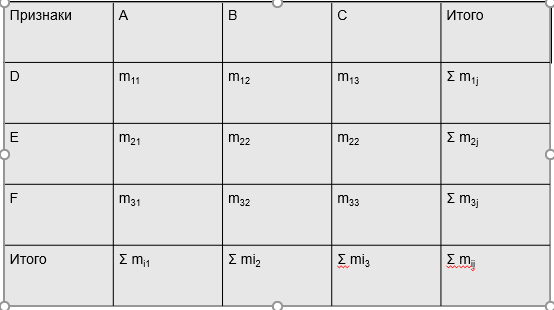   Полученное значение коэффициента сопряженности свидетельствует, что связь между условиями труда и взаимоотношениями в коллективе весьма заметна. Множественная корреляция Для оценки взаимосвязи между признаком y и несколькими факторными признаками xi используется коэффициент множественной корреляции (совокупный коэффициент корреляции, коээфициент детерминации). Для случая двух факторных признаков х1 и х2 от имеет вид: 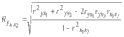 |