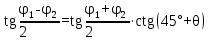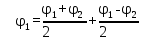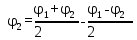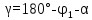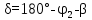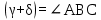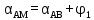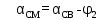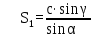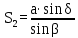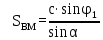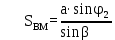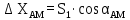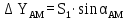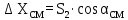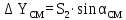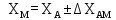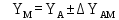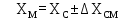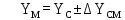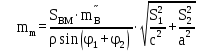тура геодезиялық кертпе. темірхан иггг. 1 зертханалы Жмыс. Тура геодезиялы кертпені есептеу 2 нса
 Скачать 47.65 Kb. Скачать 47.65 Kb.
|
|
№1 ЗЕРТХАНАЛЫҚ ЖҰМЫС. ТУРА ГЕОДЕЗИЯЛЫҚ КЕРТПЕНІ ЕСЕПТЕУ 2 нұсқа Тура геодезиялық керітпе А(XA; YA) және B(XB;YB) пункттарының координаталары және βA,βB горизонталь бұрыштары берілген болсын. А нүктесінің координаталары: XA=92808,70 YA=3584,92 В нүктесінің координаталары: XВ=92012,08 YВ=4643,85 Горизонталь бұрыштары: βA= 40°26′44″ βB= 57°43′31″ Табу керек: С(XС; YС) нүктесінің координаталарын. Шешімі: Анықталатын С нүктесі бойынша βС горизонтальдық бұрышын есептейміз: βС=180°-(βA+βB) βС=180-(40°26′44″+57°43′31″)= 81°49′45″ 2. AB жағының дирекциондық бұрышы (αАВ) және оның горизонтальдық бұрышы dAB анықталады: 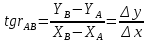 мұндағы  АВ бағытының кестелік бұрышы. АВ бағытының кестелік бұрышы.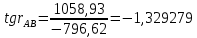 αАВ =-53°2′47″ (233°2′47″) (ІII ширек) ΔY және ΔX координаталарының мәндерінің таңбалары бойынша АВ бағыты орналасқан ширек анықталады және αАВ дирекциондық бұрышы есептеледі. АВ жағының ұзындығы: 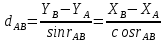 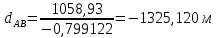 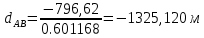 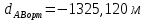 3. АВ жағының ұзындығы және βA, βB өлшенген бұрыштары арқылы синустар теоремасы бойынша үшбұрыштың басқа да жақтарының ұзындықтарын есептейміз: 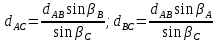 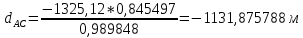 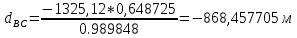 1. AC және ВС жақтарының дирекциондық бұрыштарын табамыз: 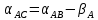 αAC=233°2′47″-57°43′31″ =175°19′16″ αBC= 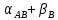 αBC=313°2′47″+40°26′44″=353°29′31″ 2. С нүктесінің координатаcының өсімшесін анықтау. А нүктесіне байланысты: ΔXAC= dAC cosαAC ΔXAC=-1131,875*(-0,996668)= 1128,103592 м ΔYAC= dAC sinαAC ΔYAC=-1131,875*0,081571=-92,328175м В нүктесіне байланысты: ΔXBC= dBC cosαBC ΔXBC=-868,457*0,993556=-862,860663м ΔYBC= dBC sinαBC ΔYBC=-868,457*(-0,113343)=98,433521м 3. С нүктесінің координатасын 2 рет есептейді. А нүктесіне байланысты: XC=XA+ΔXAC=XA+dAC*cosαAC XC=92808,70+1128,103592=92808,70+(-1131,875788)* (-0.996668)=93936,804 м YC=YA+ΔYAC=YA+dAC*sinαAC YC=3584,92+(-92,328175)=3584,92+(-1131,875788)*0,081571 =3492,592м В нүктесіне байланысты: XC=XB+ΔXBC=XB+dBC*cosαBC XC=92012,08+(-862,860663)=92012,08+(-868,457705)*0,993556=91149,219м YC=YB+ΔYBC=YB+dBC*sinαBC YC=4643,85+98,433521=4643,85+(-868,457705)*(-0,113343)=4742,284м Бұл табылған қос мән С нүктесі координатасының тексеру мәнін береді. 4. mnβ горизонталь бұрыш өлшемінің қателігін біле отырып, С нүктесінің қателігін анықтайды: 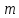 Bc= Bc=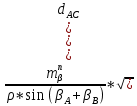 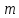 Bc= Bc=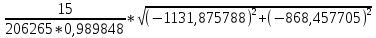 = 0,104814 = 0,104814Юнг және Гаусс формуллалары бойынша тура геодезиялық кертпені есептеу Ізделінетін нүктенің координаталарын үшбұрыштың алдын ала шешуін қажет етпейтін Юнг және Гаусс формулалары арқылы да анықтауға болады. Бұл жағдайда бастапқы пункттардың белгілі бір тәртібі сақталынуы керек. Келесі ережелерге сәйкес: егер, біз бастапқы пункттар арасына тұрып, ізделінетін С пунктына қарама-қарсы қарап тұрсақ, сол қол жақтағы бастапқы пункт - (А) - бірінші, ал оң жақтағы (В) - екінші болады (1.3 - сурет). Онда С нүктесінің координаталары үшбұрыштың ішкі бұрыштар котангенсімен анықталады (Юнг формуласы): Xc= 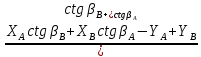 Xc= 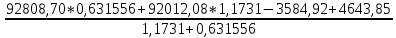 = 92877,64116 = 92877,64116Yc= 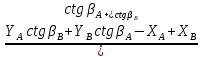 Yc= 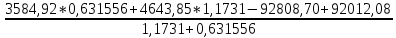 = 3831,84284 = 3831,84284C нүктесінің координаталары дирекциондық бұрыштың тангенстері мен котангенстері арқылы да анықталады (Гаусс формуласы). Егер, дирекциондық бұрыштың біреуі 0° немесе 180° жакын болса, онда С нүктесінің координаталарын дирекциондық бұрыштың тангенстер формуласымен анықтау қолайлы: Xc= 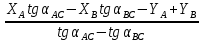 Xc= 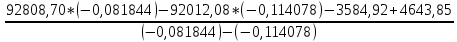 =122840,7526 =122840,7526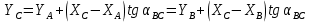 Yс=3584,92+(122840,7526-92808,70)*(-0,081844)=4643,85+(122840,7526-92012,08)*(-0,114078)=11126,976 Егер дирекциондық бұрыштың мәні 90° немесе 270° жақын болса, онда бұл дирекциондық бұрыштың үлкен мәнді тангенс үшін жоғарыдағы есептеулер бойынша қолайсыз болады. Мұндай жағдайда дирекциондық бұрыштың котангенсі формуласын қолданған тиімді: Yc= 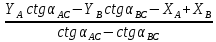 Yc= 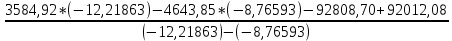 =1127,16628 =1127,16628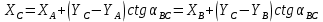 Хс=92808,70+(1127,166-3584,92)*(-12,21863)=92012,08+(1127,166-4643,85)*(-8,76593) = 122839,086 2 Кері геодезиялық кертпе Іс жүзінде жобалық берілімдерді жер бетіне қадалау (түсіру) үшін екі нүктенің тік бұрышты координаталары арқылы, олардың арасындағы сызықтың дирекциондық бұрышын жəне ұзындығын анықтауға тура келеді. Осындай есептерді шығару кері геодезиялық есептің мəнін құрайды. Кері геодезиялық есеп. Координаталары белгілі екі пункттің дирекциондық бұрышы α мен арақашықтығын d анықтау керек. Осы есепті кері геодезиялық есеп деп атайды. Кері геодезиялық керітпе жергілікті жердегі координаталары белгілі 3 немесе одан да көп пункттің бағыттары және олардың арасындағы (α, β) бұрыштарын өлшеу арқылы қосымша М нүктесін табу кезінде қолданылады. Бұл тапсырманың толық шешімін француз математигі Лорано Потенот ойлап тапқан, сондықтан нүктенің кординаталарын табудың кері керітпелік әдісін Потеноттың тапсырмасы деп атайды. Кері геодезиялық керітпе геодезиялық тірек жүйелеріндегі пункттердің теодалиттік және тахеометрлік жүрістерге байланысы кезінде қосымша белгілі бір нүктедегі φ1 (немесе φ2 ) бұрыштарын өлшеу қажет. Тәжірибеде кері керітпелер сенімді бақылау және жоғарғы дәлдікті ізделінетін нүкте координаталарын анықтау ең кем деген де бастапқы 4 пункттер арқылы жиі қолданылады. Кері геодезиялық керітпе әдісінде Потеноттың классикалық тәсілінен басқа да Кнейссельдің, Коллинстің, И. Ю. Пранис-Праневичтің, Ф. Ф. Павловтың және т.б тәсілдері кездеседі. Төменде бастапқы 3 пункт бойынша кері керітпені есептеудің Кнейссель әдісі ұсынылған. А (  )және С( )және С(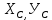 )үш пункттердің белгілі координаталары және анықталатын М нүктесіндегі өлшенген )үш пункттердің белгілі координаталары және анықталатын М нүктесіндегі өлшенген 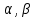 ,горизонталь бұрыштар бойынша сол нүктенің ( ,горизонталь бұрыштар бойынша сол нүктенің (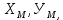 ) координаталарын табу керек. ) координаталарын табу керек.Кері геодезиялық кертпені келесі екі тәсілмен орындау керек : толық схема Есеп бойынша (Потенот тәсілі ) , Кнейсель тәсілі бойынша бақылау есептеулер.схемалары нұсқалар бойынша құрастырылады. 11-нұсқа 2-кесте Кері геодезиялық кертпе
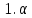 АВ дирекциондық бұрыштың шамасын есептеу: АВ дирекциондық бұрыштың шамасын есептеу:
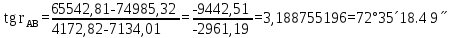 Горизонталь ұзындықтарды есептеу: 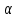 АВ = АВ =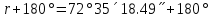 = =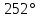 35 35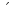 18,49 18,49
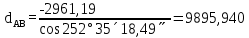
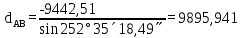
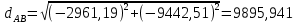
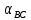 дирекциондық бұрыштың шамасын есептеу: дирекциондық бұрыштың шамасын есептеу: 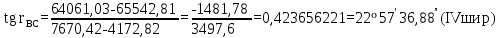 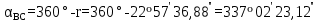
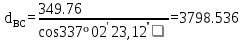
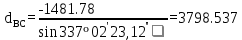
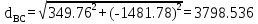 2. Екі бастапқы қабырғалар арасындағы бұрышты есептеу:
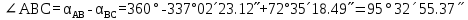 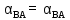 -180 -180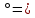 252 252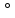 35 35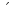 18.49 18.49 -180 -180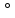 = =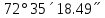 3. АВ бастапқы пункттегі 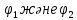 горизонталь бұрыштарды есептеу: горизонталь бұрыштарды есептеу:
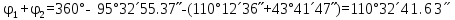 ∆АВМ және ∆СМВ анықтайды:
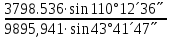 = 0,521418841 = 27 = 0,521418841 = 27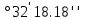
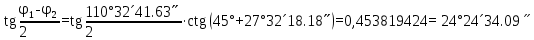
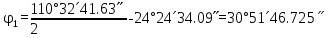 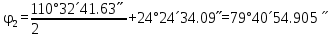 4. ∆АВМ және ∆СМВ 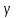 , , 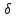 анықтайды: анықтайды:
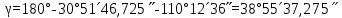
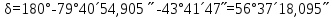
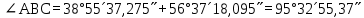 5. АМ және СМ дирекциондық бұрыштар мен S1, S2 қабырғалардың горизонталь ұзындықтарын табады:
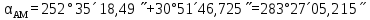
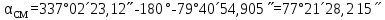
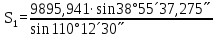 = 6625,852 = 6625,852
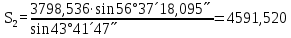
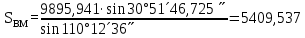
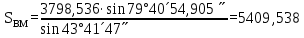 6. А және С нүктелеріне қатысты М нүктесінің координаталарын екі анықтайды, координат өсімшелерін есептеу:
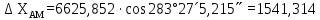
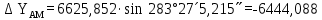
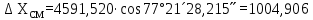
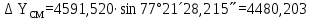
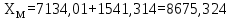
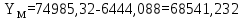
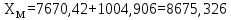
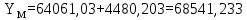 7. Қателікті есептеу:
mm 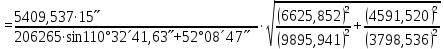 = 0,58′′ = 0,58′′ |

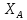
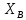
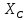
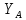
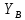
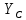
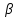
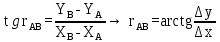
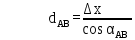
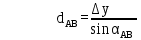
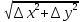
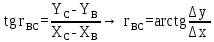
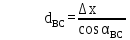
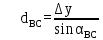
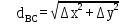
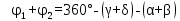
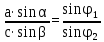 =ctgθ
=ctgθ