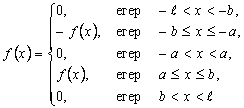№ 10 дәріс Фурье қатары
Мазмұны: Функцияларды тригонометриялық Фурье қатарына жіктеу.
Дәрістің мақсаты: Серпіліс анализінде қолданылатын Фурье қатары ұғымын беру, функцияларды Фурье қатарына жіктеу мысалдарын келтіру.
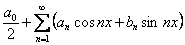 (10.1) (10.1)
түріндегі функциялық қатар 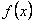 функциясының Фурье қатары деп аталады, мұндағы функциясының Фурье қатары деп аталады, мұндағы 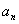 , , 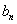 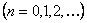 коэффициенттері коэффициенттері
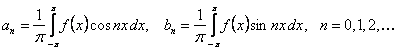 (10.2) (10.2)
формулалары бойынша анықталады. Ескерте кететін жайт: әр уақытта да 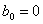 . (10.1) қатарының мүшелерін амплитудасы . (10.1) қатарының мүшелерін амплитудасы 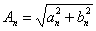 , жиілігі , жиілігі 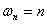 және фазасы және фазасы 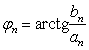 болатын, болатын,
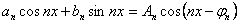
гармоникалар түрінде жазуға болады.
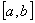 -ны -ны 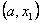 , , 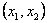 , , 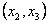 , ,  , , 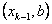 ( (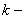 ақырлы сан) интервалдарға бөлгенде, олардың әрқайсысында ақырлы сан) интервалдарға бөлгенде, олардың әрқайсысында 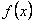 монотонды болса, монотонды болса, 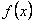 функциясы функциясы 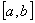 кесіндісінде үзінді-монотонды деп аталады. кесіндісінде үзінді-монотонды деп аталады.
10.1 теорема Егер 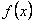 периодты (периоды периодты (периоды 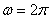 ), үзінді-монотонды және ), үзінді-монотонды және 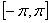 кесіндісінде шенелген болса, онда оны Фурье қатары кез келген кесіндісінде шенелген болса, онда оны Фурье қатары кез келген 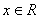 нүктесінде жинақты, ал қосындысы нүктесінде жинақты, ал қосындысы 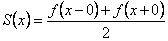 болады. болады.
Теоремадан 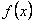 функциясының үзіліссіз болу нүктелерінде функциясының үзіліссіз болу нүктелерінде 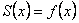 теңдігі орындалатыны түсінікті. теңдігі орындалатыны түсінікті. 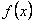 -тің бірінші текті үзіліс нүктелерінде Фурье қатарының қосындысы функцияның оң жақты және сол жақты шектерінің арифметикалық орташасына тең болады. -тің бірінші текті үзіліс нүктелерінде Фурье қатарының қосындысы функцияның оң жақты және сол жақты шектерінің арифметикалық орташасына тең болады.
Егер 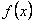 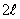 -периодты функция болса, оның Фурье қатары -периодты функция болса, оның Фурье қатары
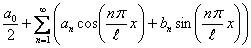 (10.3) (10.3)
түрінде жазылады, мұндағы
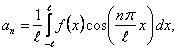 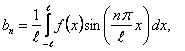 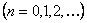 . (10.4) . (10.4)
10.2 теорема
Егер периоды 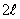 болатын периодты болатын периодты 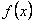 функциясы функциясы 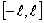 кесіндісінде үзінді-монотонды және шенелген болса, онда оның (10.3) түріндегі Фурье қатары кез келген кесіндісінде үзінді-монотонды және шенелген болса, онда оның (10.3) түріндегі Фурье қатары кез келген 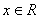 үшін үшін
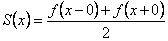
қосындысына жинақталады.
Егер периодты 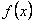 функциясы жұп болса, онда ол Фурье қатарына тек косинустар бойынша жіктеледі, яғни функциясы жұп болса, онда ол Фурье қатарына тек косинустар бойынша жіктеледі, яғни 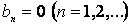 , ал , ал
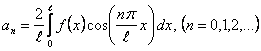 . .
Егер де периодты 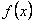 – тақ функция болса, онда ол Фурье қатарына тек синустар бойынша жіктеледі, яғни – тақ функция болса, онда ол Фурье қатарына тек синустар бойынша жіктеледі, яғни 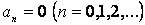 , ал , ал
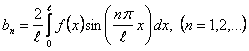 . .
Әрбір 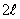 -периодты -периодты 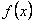 функциясы және кез келген функциясы және кез келген 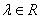 саны үшін саны үшін
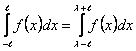
теңдігі орындалған соң, Фурье коэффициенттерін
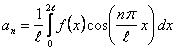 , , 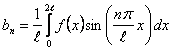 , ,
мұндағы 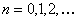 , формулалары бойынша есептеуге болады. , формулалары бойынша есептеуге болады.
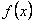 функциясы функциясы 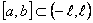 кесіндісінде үзінді-монотонды және шенелген болсын. Бұл функцияны Фурье қатарына жіктеу үшін оны кесіндісінде үзінді-монотонды және шенелген болсын. Бұл функцияны Фурье қатарына жіктеу үшін оны 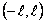 ин-тервалына, осы интервалда үзінді-монотонды және шенелген болатындай етіп, жалғастырамыз. Табылған функцияны ин-тервалына, осы интервалда үзінді-монотонды және шенелген болатындай етіп, жалғастырамыз. Табылған функцияны 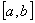 -да берілген функцияға жинақтала-тын Фурье қатарына жіктейміз. Егер берілген функцияны -да берілген функцияға жинақтала-тын Фурье қатарына жіктейміз. Егер берілген функцияны 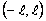 интервалына жұп түрінде жалғастырсақ, онда оның тек косинустар бойынша жіктелуін аламыз, ал егер тақ түрінде жалғастырсақ, онда интервалына жұп түрінде жалғастырсақ, онда оның тек косинустар бойынша жіктелуін аламыз, ал егер тақ түрінде жалғастырсақ, онда 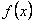 -тың тек синустар бойынша жіктелуін аламыз. -тың тек синустар бойынша жіктелуін аламыз.
Мысалы, 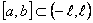 аралығында анықталған және аралығында анықталған және 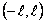 -де -де
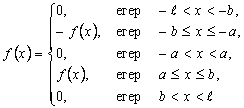
теңдіктеріне сәйкес жалғастырылған 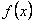 функциясы тек синустар бойынша жіктеледі. Мұндай функцияның Фурье қатарының функциясы тек синустар бойынша жіктеледі. Мұндай функцияның Фурье қатарының 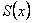 қосындысы қосындысы 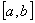 ішінде ішінде 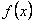 -ке тең және 10.2 теоремасы бойынша -ке тең және 10.2 теоремасы бойынша 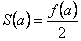 , , 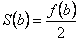 болады. болады.
Фурье қатары 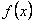 -тің үзіліссіз болу нүктелерінде функцияның сәйкес мәндеріне жинақталған соң, Фурье қатарларын сандық қатарлардың қосындысын табу үшін пайдаланады. Мысалы, егер -тің үзіліссіз болу нүктелерінде функцияның сәйкес мәндеріне жинақталған соң, Фурье қатарларын сандық қатарлардың қосындысын табу үшін пайдаланады. Мысалы, егер 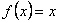 функциясының функциясының 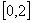 -гі косинустар бойынша жіктелуің алсақ, төмендегі теңдікті аламыз -гі косинустар бойынша жіктелуің алсақ, төмендегі теңдікті аламыз
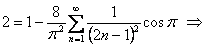 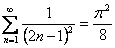 . . |
 Скачать 48.96 Kb.
Скачать 48.96 Kb.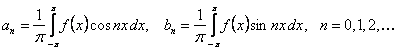 (10.2)
(10.2)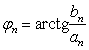 болатын,
болатын,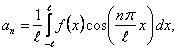
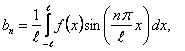
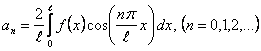 .
.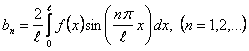 .
.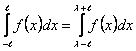
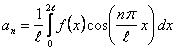 ,
, 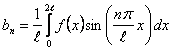 ,
,