11. Перпендикулярность прямой и плоскости Признак перпендикулярности прямой и плоскости
 Скачать 129 Kb. Скачать 129 Kb.
|
|
11. Перпендикулярность прямой и плоскости Признак перпендикулярности прямой и плоскости: прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, принадлежащим данной плоскости. 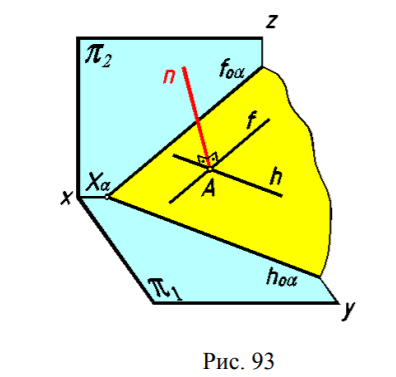 На чертеже в качестве пересекающихся прямых плоскости выбирают произвольные горизонтали и фронтали этой плоскости, чтобы можно было использовать частный случай проецирования прямого угла (рис.93). 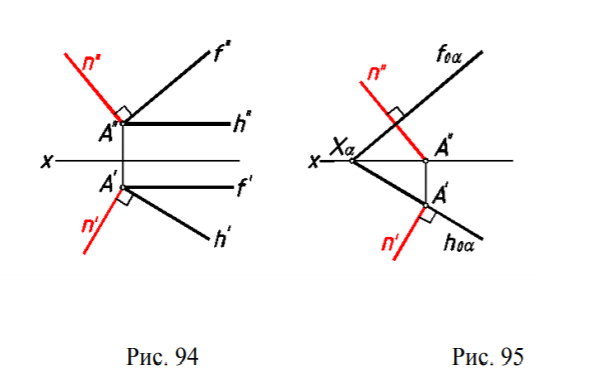 Тогда признак перпендикулярности прямой и плоскости на чертеже можно сформулировать следующим образом: если горизонтальная проекция прямой перпендикулярна горизонтальной проекции горизонтали плоскости, а фронтальная проекция этой прямой перпендикулярна фронтальной проекции фронтали этой плоскости, то такие прямая и плоскость в пространстве взаимно перпендикулярны (рис.94 и 95) На рис. 94 прямая n и плоскость, заданная горизонталью h и фронталью f взаимно перпендикулярны, т.к. n h и n h . На рис. 90 прямая n перпендикулярна плоскости, заданной следами, поскольку следы плоскости являются ее горизонталью и фронталью. Расстояние от точки до плоскости Расстояние от точки до плоскости равно длине перпендикуляра, опущенного из точки на эту плоскость. 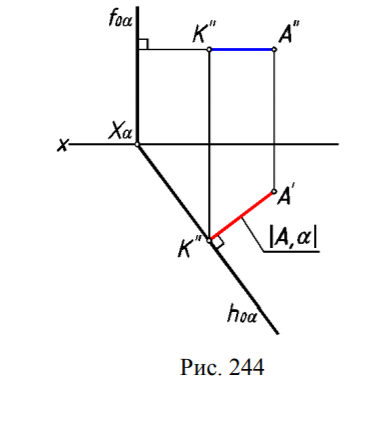 На рис.244 плоскость α перпендикулярна горизонтальной плоскости проекций. Отрезок АК, определяющий расстояние от точки А до плоскости α, параллелен плоскости проекций π1 и проецируется на неё в натуральную величину. 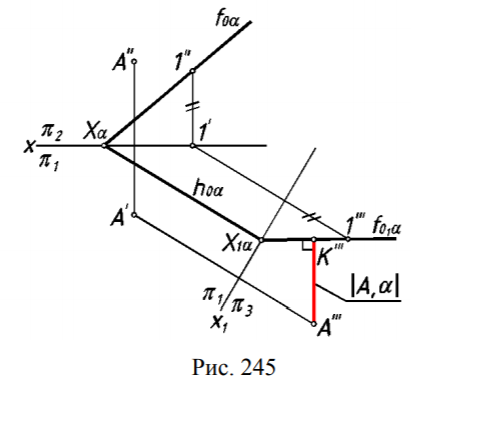 На рис.245 плоскость α занимает общее положение относительно плоскостей проекций. Поэтому целесообразно, сначала заменой плоскостей проекций преобразовать чертеж так, чтобы плоскость стала перпендикулярна новой плоскости проекций π3. |
