14. Издержки и прибыль. Минимизация издержек. Максимизация прибыли. Траектория расширения производства. Лемма Шепарда и спрос на факторы производства
 Скачать 289.03 Kb.
|
|
14. Издержки и прибыль. Минимизация издержек. Максимизация прибыли. Траектория расширения производства. Лемма Шепарда и спрос на факторы производства. Издержки и прибыль Функция общих (валовых) издержек:  - Функция общих издержек является неявной функцией, задающей кривую равных общих издержек – изокосту Функция выручки:  Функция прибыли:  Задача минимизации издержек, необходимых для выпуска 𝑞0 единиц продукции при ценах труда и капитала 𝑤 и 𝑣, соответственно, решается с помощью функции Лагранжа: 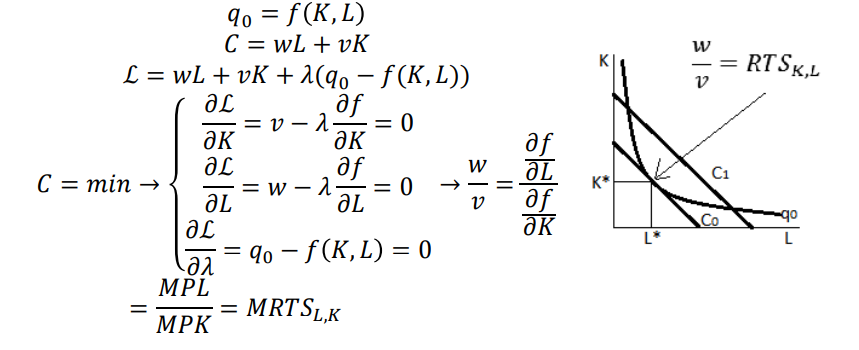 Траектория расширения производства  Объем выпуска, спрос на факторы и лемма Шепарда Поскольку оптимальный набор факторов определяется из решения задачи ограниченной оптимизации, в которой ограничением является объем выпуска, очевидно, что объемы спроса на факторы задаются функциями, зависящими, помимо прочего, от объемов выпуска Соответственно, для нахождения величин спроса на факторы мы можем использовать лемму Шепарда: 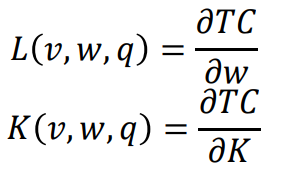 Если бы при изменении цены фактора не происходило замещение между факторами, то график функции валовых издержек имел бы вид прямой линии  . Однако в реальности имеет место замещение, так что кривая валовых издержек имеет вид 𝑇𝐶 Из смысла производной следует, что производная функции валовых издержек показывает, на сколько увеличатся валовые издержки при увеличении на 1 единицу цены фактора производства Следовательно, производная функции валовых издержек по цене фактора и есть объем использования данного фактора. 21. Теория обусловленных (контингентных) благ. Рынок страхования с точки зрения теории обусловленных (контингентных) благ. Обусловленные (контингентные) блага – это блага, которые индивид получает только при определенном стечении обстоятельств (то есть при определенном «состоянии мира») Понятие обусловленных (контингентных) благ можно использовать при рассмотрении ситуаций, связанных с рисками Если индивид владеет автомобилем стоимостью в 1 млн руб. и иным имуществом на сумму 9 млн руб., то величину имущества индивида в будущем периоде можно считать обусловленным (контингентным) благом. Так, если его машина не будет угнана, то в будущем периоде общая стоимость имущества 𝑊𝑔 индивида составит 10 млн руб. (мы абстрагировались от проблемы утери автомобилем своей товарной стоимости) С другой стороны, если его машина все же будет угнана, то в будущем периоде общая величина имущества 𝑊𝑏 индивида составит 9 млн руб. Если вероятность угона машины в течение рассматриваемого периода времени составляет 1 − 𝑝, то ожидаемая общая стоимость имущества индивида в будущем периоде будет равна:  Страховой рынок как рынок обусловленных (контингентных) благ. Индивид изначально находится в точке A в состоянии неопределенности: с вероятностью 𝑝 стоимость его имущества в будущем периоде составит  (то есть останется такой же, как в текущем периоде), а с вероятностью (1 − 𝑝) составит  Математическое ожидание стоимости имущества индивида в будущем периоде тогда равно:  Данное равенство превратится в уравнение линии ожидаемой стоимости, если заменить  В точке B пересечения линии ожидаемой стоимости с линией уверенности находится безрисковая стоимость  имущества в будущем периоде при условии справедливого страхования Предположим, что индивид не склонен к риску – так что его кривая безразличия выпукла к началу координат – тогда очевидно, что в точке B его полезность выше, чем в исходной точке При этом тот же уровень полезности 𝑢0, что и при исходной рисковой ситуации (т.е. в точке A), данный индивид получит при безрисковой стоимости  (т.е. в точке C) В таком случае справедливая цена страховки равна  А максимальная (резервная) цена, по которой индивид готов купить страховку, равна 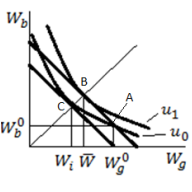  |