решение задач. Макаров В.Ю ЗРЭА-21-17 решение задач. 2. 25. Плоская электромагнитная волна с линейной поляризацией падает на границу раздела между средой показателем преломления 1,5 и вакуумом

• Название: 2. 25. Плоская электромагнитная волна с линейной поляризацией падает на границу раздела между средой показателем преломления 1,5 и вакуумом
• Анкор: решение задач
• Дата: 31.01.2021
• Размер: 92.7 Kb.
• Имя файла: Макаров В.Ю ЗРЭА-21-17 решение задач.docx
• Тип: Документы; #172894

1.6 Определите характеристическое сопротивление металла с удельной электрической проводимостью 6·107 См/м и относительной магнитной проницаемостью μ =1 на частотах 10 кГц и 1 МГц

Ответ: 25,6·10^-6 (1 – j) Ом, 25,6·10^-5 (1 – j) Ом.

2.25. Плоская электромагнитная волна с линейной поляризацией падает на границу раздела между средой – показателем преломления 1,5 и вакуумом. Вектор напряженности электрического поля образует с плоскостью падения угол 45°. Определите вид поляризации отражения волны, если угол падения равен 45°.
Для этих волн, комплексная амплитуда определяется из выражения:

E 2Em sin cos(gx)exp( jhz) x0				j2Em cos sin( gx)exp( jhz) z0	,
где h = 0sin , g = 0cos , 0		2	.
		0

Из выражения для находим E :

E z

Ez = 2Emcos sin(gx)exp(jhz).

Запишем граничные условия для безграничных пластин из идеального металла:

а) Ez(x = 0) = E = 0;

б) Ez(x = a) = E = 0.

Из условия б) получим:

Ez(x = a) = 2Emcos sin(ga)exp(jhz) = 0.

Откуда следует, что:

sin(ga) = 0;	ga	2 cos a	n ,
		0

где n может быть нулём или принимать любые целочисленные значения. Из последнего выражения находим:

cos

n 0

.

2a

Поскольку cos 1, то и

n 0

1, то есть:

2a

n 0

1;

2 a

.

0

2a

n

Ответ:

2 a

, где n – целое число.

0

n

Задача 3.5

Определить критическую длину волны, критическую частоту и длину волны в прямоугольном волноводе для волны типа Е11. Размеры поперечного сечения волновода 4х3 см. Частота колебаний 10 ГГц, скорость электромагнитной волны 3*10⁸ м/с.
Мода волны E11 имеет номера m=1и n=2.

Критическая частота для данной моды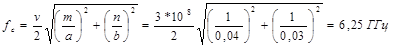



Отсюда критическая длина волны равна



а длина волны в свободном пространстве


Найдем длину волны в волноводе


4.25. В коаксиальной линии передачи С размерами поперечного сечения d = 9 мм, D = 21 мм распространяется волна типа Т. Определите предельную передаваемую мощность, если пробой происходит при напряженности электрического поля 30 кВ/см. Диэлектрик воздух.

Если волновой размер антенны составляет одну длину волны, максимальные фазовые искажения не должны превышать π/8, а в качестве приемной используется абсолютно ненаправленная изотропная антенна, зона Френеля для антенны начинается с волнового расстояния (r/λ):
• 0.75.
5.6. Определите длины волн типов H1 и Н2, распространяющихся вдоль диэлектрической пластины толщиной 10 мм с относительной проницаемостью  = 2,8 при частоте поля 12 ГГц.

Волна распространяется вдоль спирали с размерами а = 5 мм, д = 2 мм (см. рис. 8.6). Частота поля 3 ГГц. Определить фазовую скорость по приближенной формуле (8.19) и по уточненной формуле (8.17). Оценить погрешность приближенной формулы. При каких значениях параметров спирали приближенная формула позволяет определить отношение цап а погрешностью ие более 1067 Р е ш е н и е. Тангенс угла наклона витков спирали 18 а = — = 0,06375.

6.25. Прямоугольный резонатор с размерами a, b, l возбуждается тонким штырем на резонансной частоте колебания типа Е110. Добротность резонатора E110 Q известна. Длина штыря lд, координаты его основания ( a 2 , b 2 , 0). Распределение электрического тока по штырю считать постоянным (lд << 0 ) амплитуда тока I0. Определите комплексную амплитуду напряженности электрического поля в резонаторе.
Низшее (основное) колебание имеет наибольшую резонансную длину волны. В прямоугольном резонаторе основным колебанием при b < а и b < l является H101, при а < b и , а при и Обычно наименьшим размером является b.



Рис. 2.9. Структура электромагнитного поля Н101 колебания в некоторый момент времени 0
Поэтому наиболее часто используется колебание H101. Структура электромагнитного поля этого колебания в некоторый момент времени показана на рис. 2.9.

Собственная добротность резонатора с колебанием Н101 может быть определена из формулы (2.16). Выполнив необходимые преобразования, получаем:

(2.29)

Как показывает расчет, собственная добротность прямоугольного резонатора достигает десятков тысяч в сантиметровом диапазоне волн.

7.6. Вычислите ширину основного лепестка диаграммы направленности излучающей системы, описанной в задаче 7.5, при следующих параметрах: f = 250 МГц, l = 0,8 м.
Ширину диаграмм направленности по нулевому излучению в вертикальной 2₀ плоскости можно рассчитать по формуле: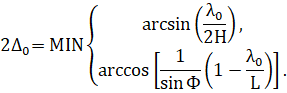



Подставив значения, получим следующее:



Следовательно, ширина диаграммы направленности по нулевому излучению в вертикальной плоскости равна: