задачи. Задание 1-6 с решением. 2 3 4 Решение
 Скачать 56.94 Kb. Скачать 56.94 Kb.
|
|
Задание 1. Лодка должна попасть на противоположный берег по кратчайшему пути (в системе отсчета, связанной с берегом). Модуль скорости течения реки u, а модуль скорости лодки относительно воды v. Модуль скорости лодки относительно берега должен быть равен 1) 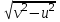 2) 2) 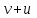 3) 3) 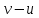 4) 4) 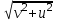 Решение: По закону сложения скоростей, вектор скорости лодки относительно берега (неподвижной системы отсчета) равен сумме скорости лодки относительно воды (подвижной системы отсчета) и скорости течения воды (переносной скорости). По условию, вектор скорости лодки в системе отсчета, связанной с берегом, должен быть перпендикулярен ему. 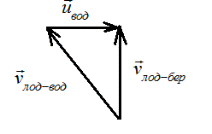 Построив «треугольник скоростей» из теоремы Пифагора для скорости лодки относительно берега имеем Ответ: 1) 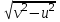 Задание 2. Уравнение движения материальной точки x = 4t + 2t2 . Запишите уравнение скорости и вычислите скорость через 10 с от начала движения. Решение: Уравнение движения материальной точки: Х = х0 + V0 ∙ t + а ∙ t2 / 2 Сравнивая с нашим уравнением: а = 4м/с2; V0 = 4 м/с; х0 = 0 Получаем: X = 4t + 2t2 уравнение скорости в общем виде: Vx(t) = V0 + а ∙ t Подставив в него численные значения, найдем уравнение скорости данного движения: Vx(t) = 2 + 8t Через 10 с скорость будет равна: v (10) = 4 + 4 ∙ 10 = 44 м/с Ответ: Vx(t) = 4+ 2t; v (10) = 44 м/с Задание 3. Уравнение скорости материальной точки Vx = 4 + 2t. Запишите уравнение движения, если в начальный момент времени точка находилась в начале координат Решение: Уравнение скорости v = 4 + 2t Откуда V0 = 4 м/с; а = 2м/с2 Уравнение движения материальной точки: X = 4t + t2 Ответ: x (t) = 4t + t2 Задание 4. Определить по графику зависимости скорости от времени путь, пройденный телом, и среднюю скорость на всем пути 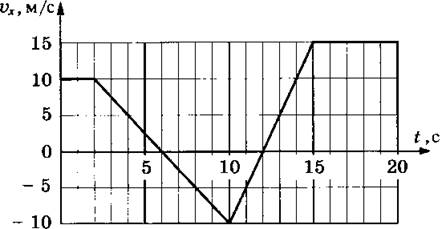 Решение: Среднюю скорость можно найти по формуле: где S – путь, пройденный телом за время t = 20 c. Путь S можно найти как площадь под графиком скорости (площадь прямоугольника + площадь треугольника+ площадь треугольника + площадь треугольника + площадь треугольника + площадь прямоугольника), имеем: S = 2 ∙ 10 + ½ ∙ 4 ∙ 10 + ½ ∙ 5 ∙ 10 + ½ ∙ 2 ∙ 10 + ½ ∙ 3 ∙ 15 + 5 ∙ 15 = 172,5 м и средняя скорость, равна: ν = 172,5 / 20 = 8,625 м/с Ответ: 8,625 м/с Задание 5. Материальная точка движется по окружности радиуса R. Закон ее движения задается уравнением S=At+Bt2+Ct3. Определить скорость, тангенциальное, нормальное и полное ускорение в момент времени t1
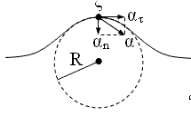 Решение: Уравнение имеет вид: S = 5t‒3t2 тангенциальное ускорение найдем, взяв первую производную от скорости во времени: аτ = dν / dt = ‒ 2В = 6 м/с2 Нормальное ускорение рассчитывается по формуле: ап = ν2 / R ν = dS/dt = ‒ 6 ∙ t ап = (‒ 6 ∙ t)2 / R = (‒ 6 ∙ 3)2 / 10 = 32,4 м/с2 Полное ускорение является геометрической суммой ускорений ап и аτ. Абсолютное значение ускорения равно: 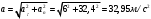 Ответ: ап =32,4 м/с2; аτ = 6 м/с2; а = 32,95 м/с2 Задание 6. По горизонтальным рельсам движется платформа с песком со массой М скоростью v 1. В песок попадает снаряд массой m. В момент попадания снаряда скорость снаряда равна v2 и направлена под угломα к горизонту. После попадания снаряда платформа стала двигаться со скоростью v. Определить величины, указанные в таблице знаком вопроса.
Решение. Платформа приобретает скорость и в результате взаимодействия со снарядом. Закон изменения силы этого взаимодействия x во времени и само время взаимодействия неизвестны. На систему платформа — снаряд действуют внешние силы: сила тяжести, сила нормальной реакции рельсов и сила трения. Вследствие негоризонтального направления скорости снаряда сила нормальной реакции, действующая на платформу, во время взаимодействия платформы и снаряда изменяется и будет тем больше, чем больше внутренняя сила взаимодействия снаряда и платформы. Если пренебречь действием силы трения на платформу во время удара, то, поскольку силы тяжести и нормальной реакции рельсов строго вертикальны, можно считать, что проекция вектора импульса системы на горизонтальное направление остается постоянной. Это позволит найти скорость и, которую приобретает платформа после удара. Если ввести ось Xпо направлению движения платформы, то 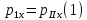 где 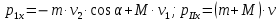 — проекции вектора импульса системы на ось X соответственно до и после взаимодействия тел. Тогда уравнение (1) примет вид 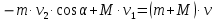 Откуда 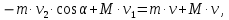 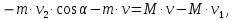 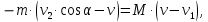 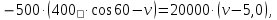 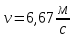 Ответ: 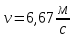 | ||||||||||||||||||||||||||||||||||||
