биофиз уравнение. 2. 55) где s смещение колеблющихся точек в волне относительно их положения равновесия, y координата положения равновесия какойлибо точки, скорость распространения волны (фазовая скорость). Интенсивность волны (плотность потока энергии) , 56)
 Скачать 26.82 Kb. Скачать 26.82 Kb.
|
|
Уравнение плоской упругой волны s 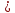 A cos A cos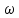 (t—y/ʋ), (2.55) (t—y/ʋ), (2.55)где s – смещение колеблющихся точек в волне относительно их положения равновесия, y – координата положения равновесия какой-либо точки, ʋ – скорость распространения волны (фазовая скорость). Интенсивность волны (плотность потока энергии) Ӏ 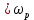 ʋ, (2.56) ʋ, (2.56)где 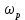 – объемная плотность энергии колебательного движения, – объемная плотность энергии колебательного движения, ʋ – скорость волны. Объемная плотность энергии упругой волны, распространяющейся в веществе, 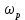 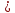 ρ ρ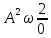 /2, (2.57) /2, (2.57)где ρ – плотность вещества. Частота колебаний, воспринимаемая наблюдателем (эффект Доплера): ν’ 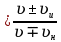 ν, (2.58) ν, (2.58)где 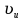 и и 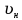 – скорости наблюдателя и источника упругой волны относительно среды, ʋ – скорость распространения волны в этой среде, ν – частота испускаемых колебаний. Верхние знаки в (2.58) соответствуют встречному движению наблюдателя и источника, нижние – движению в противоположные стороны. Доплреровский сдвиг частоты. – скорости наблюдателя и источника упругой волны относительно среды, ʋ – скорость распространения волны в этой среде, ν – частота испускаемых колебаний. Верхние знаки в (2.58) соответствуют встречному движению наблюдателя и источника, нижние – движению в противоположные стороны. Доплреровский сдвиг частоты.νд 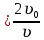 ν, (2.59) ν, (2.59)где 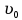 – скорость движущегося тела, ʋ – скорость волны (ультразвука). Формула получена в предположении ʋ – скорость движущегося тела, ʋ – скорость волны (ультразвука). Формула получена в предположении ʋ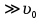 . Связь интенсивности звука и звукового давления для плоской волны. . Связь интенсивности звука и звукового давления для плоской волны.Ӏ 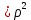 /(2ρʋ),(2.60) /(2ρʋ),(2.60)где ρ – плотность среды, в которой распространяется звук, ʋ – его скорость. Бел (Б) – в общем случае единица логарифмической относительной величины (логарифма отношения двух одноименных физических величин). Так, например, 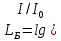 ), ), 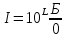 , (2.61) , (2.61)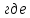 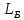 – выраженный в белах уровень интенсивности – выраженный в белах уровень интенсивности 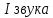 относительно относительно 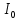 , принятого за начальный уровень шкалы, или в децибилах (дБ) , принятого за начальный уровень шкалы, или в децибилах (дБ)____________ §2.2 ● 54 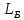 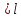 0 0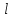 g ( g ( 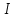 / /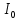 ). ). 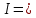 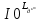 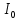 , (2.62) , (2.62)Из (2.60) и (2.61) следует 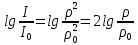 . (2.63) . (2.63) Считают, что шкалы громкости (Е) и интенсивности звука (L) совпадают на частоте 1 кГц: 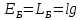 ( ( 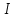 / /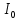 ) (2.64) ) (2.64) или в фонах 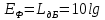 ( ( 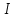 / /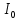 ). (2.65) ). (2.65)Соответствие между интенсивностью и громкостью звука на разных частотах можно найти по кривым равной громкости (рис. 2.3). 2.37. Напишите уравнение гармонического колебания, если амплитуда ускорения 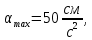 частота колебания частота колебания 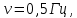 смещение точки от положения равновесия в начальный момент времени смещение точки от положения равновесия в начальный момент времени 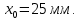 Найдите амплитуду скорости. Найдите амплитуду скорости.2.38. Напишите уравнение гармонического, если амплитуда скорости 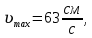 период колебаний T период колебаний T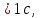 смещение точки от положения равновесия в начальный момент времени равно нулю. Найдите амплитуду ускорения, частоту колебаний. смещение точки от положения равновесия в начальный момент времени равно нулю. Найдите амплитуду ускорения, частоту колебаний.2.39. Маятник совершает гармонические колебания. Через какое время он при первом колебании отклонится от положения равновесия на расстояние, равное ½ амплитуды, если период колебания T 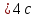 , начальная фаза , начальная фаза 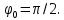 2.40. Материальная точка массой m 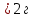 совершает гармонические колебания. В некоторый момент времени смещение точки x совершает гармонические колебания. В некоторый момент времени смещение точки x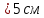 , скорость ʋ , скорость ʋ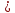 20 см/с, ускорение a 20 см/с, ускорение a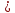 80 см/ 80 см/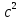 . Найдите кругувую частоту, период, фазу колебания в заданный момент времени, а также амплитуду и полную энергию колеблющейся точки. . Найдите кругувую частоту, период, фазу колебания в заданный момент времени, а также амплитуду и полную энергию колеблющейся точки.2.41. Начальная фаза колебаний точки равна нулю, период колебания T 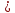 1 c. Определите ближайшие моменты времени, в которые смещение, скорость и ускорение вдвое меньше амплитудных значений. 1 c. Определите ближайшие моменты времени, в которые смещение, скорость и ускорение вдвое меньше амплитудных значений.____________ Гл.2 ● 55 2.83. Определите разность фаз в пульсовой волне между двумя точками артерии, расположенными на расстоянии 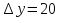 см друг от друга. Скорость пульсовой волны считать равной см друг от друга. Скорость пульсовой волны считать равной 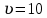 м/с, а м/с, а колебания сердца – гармоническими с частотой 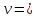 1,2 Гц. 1,2 Гц.2.84. Разность хода звуковых волн, приходящих в левое и правое ухо человека, составляет 1 см. Определите сдивиг фаз между обоими звуковыми ощущениями для тона с частотой 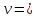 1000 Гц. 1000 Гц.2.85. Интенсивность плоской волны в воздухе равна 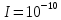 Вт/ Вт/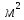 . Найдите амплитуду колебаний . Найдите амплитуду колебаний частиц (молекул) воздуха при нормальных условиях и объемную плотность энергии колебательного движения для частот 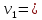 20 Гц, 20 Гц, 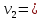 1000 Гц, 1000 Гц, 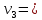 20 000 Гц. Скорость звука в 20 000 Гц. Скорость звука в воздухе 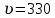 м/с. м/с. 2.86. Известно, что человеческое ухо воспринимает упругие волны в интервале частот от 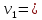 20 Гц до 20 Гц до 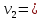 20 кГц. Каким длинам волн соответствует этот интервал в воздухе? В воде? Скорости в 20 кГц. Каким длинам волн соответствует этот интервал в воздухе? В воде? Скорости в воздухе и воде равны соответственно 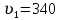 м/с и м/с и 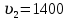 м/с. м/с. 2.87. Изучение движение барабанной перепонки показало, что скорость колебания ее участков оказывается величиной одного порядка со скоростью смещения молекул воздуха при распространении плоской волны. Исходя из этого, вычислите приближенно амплитуду колебания участков барабанной перепонки для двух случаев: а) порог слышимости; б) порог болевого ощущения. Частота равна 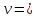 1 кГц. 1 кГц.2.88. Определите среднюю силу, действующую на барабанную перепонку человека (площадь S 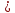 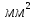 ) для двух случаев: а) порог слышимости; б) порог болевого ощущения. Частота равна ) для двух случаев: а) порог слышимости; б) порог болевого ощущения. Частота равна 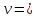 1 кГц. 1 кГц.2.89. Две машины движутся навстречу друг другу со скоростями 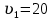 м/с и м/с и 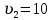 м/с. Первая м/с. Первая машина дает сигнал с частотой 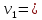 800 Гц. Какой частоты сигнал услышит водитель второй 800 Гц. Какой частоты сигнал услышит водитель второй машины: а) до встречи машин: б) после встречи машин. 2.90. Одинаковой ли высоты будет звук в случаях: а) источник звука движется навстречу наподвижному наблюдателю со скоростью 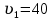 м/с? б) наблюдатель движется навстречу м/с? б) наблюдатель движется навстречунеподвижному источнику с той же скоростью? Частота источника звука 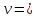 600 Гц. 600 Гц.2.91. На сколько увеличилась громкость звука, если интенсивность звука увеличилась от порога слышимости в 1000 раз. Задачу решить для звука частотой: а) 100 Гц; б) 1 кГц. Для решения воспользоваться кривыми равной громкости. _____________§2.2_●_60'>____________ §2.2 ● 60 2.92. Два звука одинаковой частоты 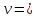 1 кГц отличаются по громкости на 1 кГц отличаются по громкости на 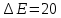 фон. Во сколько раз фон. Во сколько разотличаются их интенсивности? 2.93. Два звука одинаковой частоты отличаются по интенсивности на 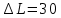 дБ. Найдите отношение дБ. Найдите отношение амплитуд звукого давления. 2.94. По условиям некоторого производства опрееделен допустимый предел уровня шума 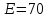 фон. фон. Определите максимально допустимую интенсивность звука. Условно считать, что шум соответствует звуку частотой 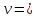 1 кГц. 1 кГц.2.95. Разрыв барабанной перепонки наступает при уровне интенсивности звука 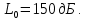 Определите интенсивность, амплитудное значение звукового давления и амплитуду смещения частиц в волне для звука частотой 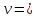 1 кГц, при которых может наступить разрыв барабанной 1 кГц, при которых может наступить разрыв барабанной перепонки. 2.96. Нормальный разговор человека оценивается уровнем громкости звука 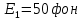 (для частоты (для частоты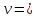 1 кГц). Определите уровень громкости звука, соответствующего трем одновременно 1 кГц). Определите уровень громкости звука, соответствующего трем одновременно говорящим людям. 2.97. Шуму на оживленной улице соответствует уровень громкости звука 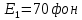 , крику , крику 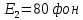 . Какой будет уровень громкости звука, полученного в результате сложения крика и шума . Какой будет уровень громкости звука, полученного в результате сложения крика и шума улицы? Считать частоту, равной 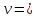 1 кГц. 1 кГц.2.98. Два звука частотой 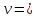 1000 Гц отличаются по громкости на 1 фон. Во сколько раз отличаются их 1000 Гц отличаются по громкости на 1 фон. Во сколько раз отличаются их интенсивности? 2.99. Шум на улице, которому соответсвует уровень интенсивности звука 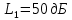 , слышен в , слышен в комнате так, как шум 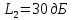 . Найдите отношение интенсивностей звука на улице и в . Найдите отношение интенсивностей звука на улице и в комнате. 2.100. Уровень громкости звука частотой 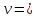 5000 Гц равен 5000 Гц равен 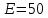 фон. Найдите интенсивность этого фон. Найдите интенсивность этого звука. 2.101. Уровни интенсивности звуков с частотами 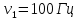 и и 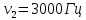 равны равны 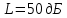 . . Определите уровни громкости этих звуков. 2.102. Звук частотой 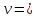 200 Гц проходит некоторое расстояние в поглощающей среде. Интенсивность 200 Гц проходит некоторое расстояние в поглощающей среде. Интенсивность звука при этом уменьшается с 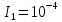 Вт/ Вт/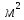 до до 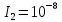 Вт/ Вт/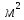 . На сколько при этом . На сколько при этом уменьшился уровень громкости? 2.103. Определите интенсивности звуков с частотами 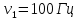 , , 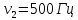 и и 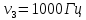 , если , если уровень громкости звуков одинаков и равен 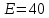 фон. фон.____________ Гл.2 ● 61 |
