2 Дріс. Сйытыты тепетедігіні диференциалды тедеуі. Те ысмды бет тедеуі. Гидростатиканы негізгі тедеуі
 Скачать 89.5 Kb.
|
|
2 Дәріс. «Сұйықтықтың тепе-теңдігінің диференциалдық теңдеуі. Тең қысмды бет теңдеуі. Гидростатиканың негізгі теңдеуі» Тепе-теңдіктегі сұйықтың диференциалдық теңдеуі тыныштық қалыптағы сұйық ішінде орналасқан кейбір нүктелері айналасынан белгіленіп алынған сұйықтың элементарлы көлемі үшін жазылады. Элементарлы көлемі кеңістіктен таңдалған координаттар өсіне параллель орналасқан dx, dy, dz, қырлы параллелипипед түрінде көрсетіледі. Ойша параллелипипедті сұйық қоршаған дей келе, олардың әсерін гидродинамикалық қысым күштеріне ауыстырып, келесіні аламыз.  (6)мұндағы: dp- гидростатикалық қысымның толық дифференциалы немесе гидростатикалық қысымның өзгеруі. Fx, Fу, Fz, - координата өстеріне сәйкес бірлік массалық күштер проекциясы; dx, dy, dz – диференциалдық теңдеу жағдайындағы параллелипипед қырлары, ол бұл теңдеудің бірінші түрі үшін тыныштықтағы сұйықтың қарастырылып отырған нүктелерінің координаталары болып табылады. (6)-теңдеуден тең қысымды беттің теңдеуін алу оңай - барлық нүктелердегі беттік қысымдар бірдей   кезінде  ал  нолге тең болуы мүмкін емес, демек . (7)Бұл теңдеу тең қысымды беттің теңдеуі болып табылады, жеке жағдайда абсолютті тыныштықтағы сұйықтың горизонтальды жазық еркін беті, ал цилиндрлік ыдыстың вертикалды өсі бойымен бір қалыпты айналатын тыныштық қалыптағы сұйықтың тең қысымды беті ретінде осы ыдыстың вертикалды өсі айналасындағы түрленген параболаның қисық сызықты беті болып табылады. 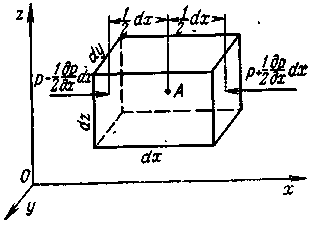 1-сурет. Гидростатиканың негізгі теңдеуіне тұжырымдама жасау Қозғалмайтын ыдыста (1-сурет) ауырлық күші әсерінде болатын сұйықты қарастырамыз. Координаталар өсін ОZ өсі вертикалды жоғары бағытта болатындай етіп орналастырамыз, яғни ауырлық күші әсер ететін сызыққа параллелді. Қарастырылып отырған сұйық көлемінің ішінен хОу жазықтығынан Z қашытыққа немесе сұйықтық еркін бетінен Н қашықтықта орналасқан А нүктесін белгілеп аламыз. Сонда біздің жағдайда координата өсіндегі бірлік массалық күштердің проекциясы келесідей:    . Бұл мәндерді (6)-теңдеуге қойсақ:  немесе интегралдағаннан кейін  мұндағы: С- интегралдау тұрақтысы. Интегралдау тұрақтысын анықтау үшін бастапқы шарттарды құрамыз: сұйықтың еркін бетіндегі, яғни Z=Z0 кезінде  , демек  бұдан  С-ның анықталған мәнін интегралдағаннан кейінгі теңдеуге қойсақ:  .Бұл сұйықтың еркін бетіне әсер ететін, сұйықтың тегіне және еркін бетінен нүктеге дейінгі арақашықтығына байланысты тыныштық қалыптағы нүктедегі қысымның негізгі гидростатикалық теңдеуі болып табылады. Бұл теңдеуде: р – сұйықтың еркін бетіне әсер ететін қысымның сыртқы абсолютті мәні,  - белгіленген нүктедегі сұйықтың бағанасындағы қысым немесе бұл шаманы салмақтың қысым деп те атайды, яғни бірлік аудандағы сұйық бағанасының салмағы мен биіктігіне (Н) тең. Ашық ыдыстарда, су қоймалары және т.б. сұйықтың еркін бетіндегі сыртқы қысымы ол атмосфералық қысым  . Бұл жағдайда, егер сұйықтың берілген нүктесіндегі абсолютті қысым атмосфералық қысымнан үлкен болса  онда ол (8) манометрлік қысым деп аталады  (9)Манометрлік қысым сұйықтың берілген нүктесіндегі атмосфералық қысымнан артық қысымды көрсетеді, сондықтан оны көбінесе артық қысым деп те атайды. (9)-теңдеу манометрлік қысымның өзгеру шегі.  кезінде  ал  кезде  , яғни манометрлік қысымның шамасы 0 ден  дейін өзгеруі мүмкін. Мұндай жағдайда, егер сұйықтың берілген нүктесіндегі абсалютті қысым атмосфералық қысымнан аз болса  , онда (9) – теңдеудің соңғы мүшесі  - Вакуумметрлік қысым (вакуум) деп аталады  (10)Вакуумметрлік қысым берілген нүктедегі атмосфераға дейінгі қысымның кемшілігін көрсетеді. Вакуумметрлік қысымның өзгеру шегі (10) теңдеуде тағайындалған, яғни  кезінде  (абсолютті вакуум), ал кезінде  демек, вакуумметрлік қысымның шамасы 0 ден  дейін өзгеруі мүмкін. Қысым Эюпрі дегеніміз қандайда – бір қарам немесе бет бойымен қысым таралуының графиктік кескіні (бейнесі). Қарам (контур) немесе бет ретінде сұйық орналасқан ыдыстың түбі немесе қабырғасы қарастырылады, ал эпюр сызығының масштабы гидростатиканың негізгі теңдеуімен анықталады.Әдебиеттер: 1 негізгі [16-23]; 2 негізгі [17-24]; 6 қосымша [30-42]. Бақылау сұрақтары
3 Сұйықтың тепе-теңдігінің дифференциалдық теңдеуіне тұжырымдама жасаңыз және теңдеудің барлық мүшелерінің физикалық мәнін түсіндіріңіз. |