Синтез счетчика. Теория автоматов Лаба1 Синтез счетчика. 2. Таблица переходов счетчика 3 Синтез счетчика на dтриггерах 4

• Название: 2. Таблица переходов счетчика 3 Синтез счетчика на dтриггерах 4
• Анкор: Синтез счетчика
• Дата: 28.09.2022
• Размер: 407.83 Kb.
• Имя файла: Теория автоматов Лаба1 Синтез счетчика .docx
• Тип: Документы; #702408
• страница: 1 из 3

Оглавление

1.Задание 2

2.Таблица переходов счетчика 3

3.Синтез счетчика на D-триггерах 4

3.1.Таблица возбуждения D –триггера 4

3.2.Таблица истинности для входов D -триггеров 4

3.3.Мнимизация функций для каждого входа D-тригеров с помощью диаграмм Вейча. (минимизируем ДНФ) 4

3.4. Приведение минимизированных формул для входов D –триггеров к базису «И-НЕ» 6

3.5.Счетчик по подулю 23 с шагом 11 на D-триггерах, комбинационная часть схемы в базисе «И-НЕ» 7

3.6.Временная диаграмма работы счетчика по модулю 23 с шагом 11 на D-триггерах 7

4.Синтез счетчика на JK -триггерах 8

4.1.Таблица возбуждения JK –триггера 8

4.2.Таблица истинности для входов каждого из JK -триггеров 8

4.3.Мнимизация функций для каждого входа JK-тригеров с помощью диаграмм Вейча. (минимизируем ДНФ) 9

4.4.Приведение минимизированных формул для входов JK –триггеров к базису «ИЛИ-НЕ» 13

4.5.Счетчик по подулю 23 с шагом 11 на JK-триггерах, комбинационная часть схемы в базисе «ИЛИ-НЕ» 14

4.6.Временная диаграмма работы счетчика по модулю 23 с шагом 11 на JK-триггерах 14

1. Задание

Построить счётчик по модулю 23 с шагом 11 в двух вариантах:
1. На D-триггерах, комбинационная часть схемы в базисе И-НЕ.
2. На JK- триггерах, комбинационная часть схемы в базисе ИЛИ-НЕ (функционал JK- триггера должен быть использован полностью, т.е. нельзя его использовать в варианте D или Т триггера).
Схемы должны быть минимизированы.

2. Таблица переходов счетчика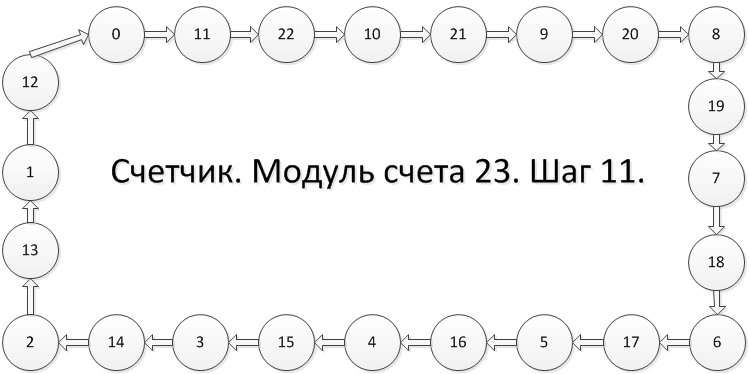

К текущему состоянию Q добавить 11(шаг) и взять остаток по модулю 23 получим состояние Q(t+1).

0	9+11=20	6+11=17	3+11=14
0+11 = 11	20+11=31/23=8	17+11=28/23=5	14+11=25/23=2
11+11 = 22	8+11=19	5+11=16	2+11=13
22+11 = 33/23=10	19+11=30/23=7	16+11=27/23=4	13+11=24/23=1
10+11 = 21	7+11=18	4+11=15	1+11=12
21+11 = 32/23=9	18+11=29/23=6	15+11=26/23=3	12+11=23/23=0

Так как нужны числа от 0 до 22, потребуется 5 разрядов, чтобы закодировать состояния счетчика, а значит ровно столько же триггеров.. 2^5 = 32 (причем, состояния с 23 по 31 не используются).

Q(t)	x4	x3	x2	x1	x0	Q(t+1)	y4	y3	y2	y1	y0
0	0	0	0	0	0	11	0	1	0	1	1
11	0	1	0	1	1	22	1	0	1	1	0
22	1	0	1	1	0	10	0	1	0	1	0
10	0	1	0	1	0	21	1	0	1	0	1
21	1	0	1	0	1	9	0	1	0	0	1
9	0	1	0	0	1	20	1	0	1	0	0
20	1	0	1	0	0	8	0	1	0	0	0
8	0	1	0	0	0	19	1	0	0	1	1
19	1	0	0	1	1	7	0	0	1	1	1
7	0	0	1	1	1	18	1	0	0	1	0
18	1	0	0	1	0	6	0	0	1	1	0
6	0	0	1	1	0	17	1	0	0	0	1
17	1	0	0	0	1	5	0	0	1	0	1
5	0	0	1	0	1	16	1	0	0	0	0
16	1	0	0	0	0	4	0	0	1	0	0
4	0	0	1	0	0	15	0	1	1	1	1
15	0	1	1	1	1	3	0	0	0	1	1
3	0	0	0	1	1	14	0	1	1	1	0
14	0	1	1	1	0	2	0	0	0	1	0
2	0	0	0	1	0	13	0	1	1	0	1
13	0	1	1	0	1	1	0	0	0	0	1
1	0	0	0	0	1	12	0	1	1	0	0
12	0	1	1	0	0	0	0	0	0	0	0