2 Тепловые свойства древесины

• Название: 2 Тепловые свойства древесины
• Дата: 27.10.2020
• Размер: 217.5 Kb.
• Имя файла: GTO-Primeri-zadachi-2-3--Teplovie-svojstva-drevesini.doc
• Тип: Документы; #146013

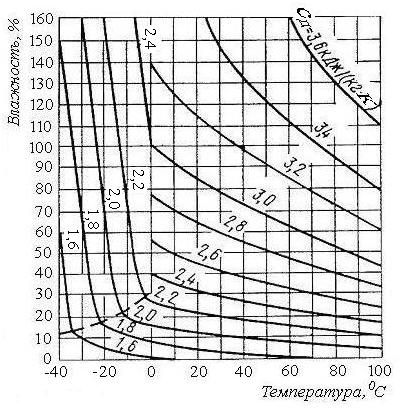
2.3. Тепловые свойства древесины

Основными параметрами, характеризующими тепловые свойства древесины, являются удельная теплоемкость, коэффициент теплопроводности и коэффициент температуропроводности.

Удельная теплоемкость с_д – это количество теплоты, необходимое для нагревания 1 кг древесины на 1⁰С (1 К). Размерность этого параметра – Дж/(кгК). Удельная теплоемкость характеризует способность материала аккумулировать тепловую энергию. Она не зависит от породы древесины. Однако температура и, особенно, влажность древесины оказывают существенное влияние на величину удельной теплоемкости. Конкретные значения этого параметра в зависимости от температуры и влажности древесины могут быть определены по диаграмме, построенной П.С. Серговским 10 в координатах W–t, приведенной на рис. 2.3.

Рис. 2.3. Диаграмма удельной теплоемкости древесины

Коэффициент теплопроводности  – это количество теплоты, проходящей через плоскую стенку площадью 1 м² и толщиной 1 м при разности температуры на противоположных сторонах стенки, равной 1⁰С (1 К). Размерность коэффициента теплопроводности – Вт/(мК). Этот параметр характеризует интенсивность перемещения теплоты в древесине. Его величина зависит от температуры, влажности, породы древесины, а также от направления теплового потока относительно древесных волокон. Определить коэффициент теплопроводности в зависимости от температуры и влажности древесины можно с помощью диаграммы, построенной в координатах –t (рис. 2.4). Диаграмма построена для березовой древесины в направлении поперек волокон (радиальном и тангенциальном). Для определения коэффициента теплопроводности древесины других пород в различных структурных направлениях надо дополнительно использовать формулу

 = нkkx, Вт/(мК),

(2.19)

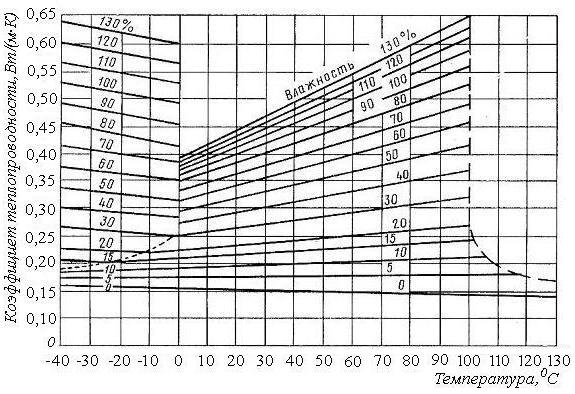
где _н – номинальное значение коэффициента теплопроводности, найденное по диаграмме на рис. 2.4, Вт/(мК); k_ – коэффициент, зависящий от базисной плотности древесины; k_x – коэффициент, зависящий от направления теплового потока относительно древесных волокон.

Рис. 2.4. Диаграмма коэффициента теплопроводности
древесины березы поперек волокон

Значения коэффициентов k_ и k_х определяют по табл. 2.1 и 2.2.

Коэффициент температуропроводности а характеризует скорость изменения температуры древесины при нестационарном теплообмене (нагревании или охлаждении). Он зависит от теплоемкости и теплопроводности древесины, а также от ее плотности:

, м2/с,

(2.20)

где с_д – удельная теплоемкость древесины, Дж/(кгК); _д – плотность древесины, кг/м³.

Табл. 2.1. Значения коэффициента k_

Базисная плотность, Б, кг/м3	350	400	450	500	550	600	650
Коэффициент k	0,81	0,87	0,93	1,00	1,11	1,26	1,45

Табл. 2.2. Значения коэффициента k_x

Группа пород древесины	Коэффициент kх при направлении теплового потока
	радиальном	тангенциальном	вдоль волокон
1. Лиственные с развитыми сердцевинными лучами (дуб, бук, граб, ольха, клен, вяз, липа)	1,00	0,87	1,60
2. Лиственные с неразвитыми сердцевинными лучами	1,00	1,00	2,00
3. Хвойные	1,00	1,00	2,20

Примеры

Пример № 42. Определить коэффициент теплопроводности древесины ольхи в тангенциальном направлении, если ее температура и влажность соответственно составляют t = 60⁰С; W = 60%.

Решение. По диаграмме на рис. 2.4 находим номинальное значение коэффициента теплопроводности _н = 0,40 Вт/(мК). Согласно табл. 4 приложения, базисная плотность ольхи составляет _Б = 420 кг/м³. Пользуясь табл. 2.1 и 2.2, определяем значения поправочных коэффициентов k_ = 0,89; k_х = 0,87. По формуле (2.19) рассчитываем коэффициент теплопроводности:

 = 0,400,890,87 = 0,31 Вт/(мК).

Ответ:  = 0,31 Вт/(мК).

Пример № 43. Определить коэффициент температуропроводности древесины граба в поперечном направлении (смешанная распиловка) при температуре t = 35⁰С и влажности W = 30%.

Решение. По табл. 4 приложения находим базисную плотность древесины граба, а затем, используя диаграмму на рис. 2.2, –
плотность древесины при влажности W = 30%: _Б = 630 кг/м³, _д = 820 кг/м³.

По диаграмме теплоемкости (рис. 2.3) определяем удельную теплоемкость древесины, а по рис. 2.4 – номинальное значение коэффициента теплопроводности с_д = 2,44 кДж/(кгК); _н = 0,275 Вт/(мК). Поправочные коэффициенты для расчета коэффициента теплопроводности находим в табл. 2.1 и 2.2. При этом учитываем, что температуропроводность происходит в поперечном направлении, т. е. коэффициент k_х определяется как среднее арифметическое двух значений – в радиальном и тангенциальном направлениях:

;

.

Коэффициент теплопроводности рассчитываем по формуле (2.19), а коэффициент температуропроводности – по формуле (2.20):

	Вт/(мК);
	м2/с.

Ответ: а = 1,7510^-7 м²/с.

Пример № 44. Перед лущением шпона круглые сортименты (кряжи) прогреваются в горячей воде от начальной температуры t_н = 5⁰С до конечной t_к = 45⁰С. В качестве сырья используется сосновая и березовая древесина влажностью W = 60%. Определить, какой породы сортименты будут прогреваться быстрее при условии, что размеры у них одинаковые.

Решение. Определяем расчетную температуру:

0С.

По табл. 4 приложения устанавливаем базисную плотность древесины обеих пород, а по рис. 2.2 – их плотность при заданной влажности _Б1 = 400 кг/м³; _д1 = 640 кг/м³; _Б2 = 500 кг/м³; _д2 = 800 кг/м³.

Используя рис. 2.3 и 2.4, находим удельную теплоемкость и номинальный коэффициент теплопроводности сосновой и березовой древесины: с_д1 = с_д2 = 2,78 кДж/(кгК); _н1 = _н2 = 0,35 Вт/(мК).

Поправочные коэффициенты определяем по табл. 2.1 и 2.2. При этом учитываем, что передача тепла происходит у круглых сортиментов в радиальном направлении: k_1 = 0,87; k_х1 = 1,00; k_2 = 1,00; k_х2 = 1,00.

По формуле (2.19) рассчитываем коэффициенты теплопроводности для древесины сосны и березы:

	1 = 0,350,871 = 0,30 Вт/(мК);
	2 = 0,3511 = 0,35 Вт/(мК).

Коэффициенты температуропроводности определяем по фор-муле (2.20):

	м2/с;
	м2/с.

Ответ: сосновые сортименты будут прогреваться быстрее,
т. к. а₁  а₂.