Конденсатор К-16360. К-16360 Расчётно-пояснительная записка. 2 Тепловой расчет конденсатора Тепловой расчет конденсатора паровой турбины, как любого теплообменного аппарата, может быть конструкторским или поверочным
 Скачать 90.73 Kb. Скачать 90.73 Kb.
|
|
2.1. Тепловой расчет конденсатора Тепловой расчет конденсатора паровой турбины, как любого теплообменного аппарата, может быть конструкторским или поверочным. Конструкторский расчёт имеет целью определение поверхности теплообмена и основных размеров проектируемого конденсатора. Расчет проводится на заводе-изготовителе турбины. Поверочный расчёт имеет целью определение параметров теплоносителей спроектированного или действующего конденсатора. Расчет проводится на заводе-изготовителе турбины при расчете переменного режима работы конденсационной установки и ПТУ в целом, а также сотрудниками электростанций для уточнения эксплуатационных характеристик конденсатора. Текущий поверочный расчет осуществляется также на электростанциях, имеющих АСУ. В основе методики как конструкторского, так и поверочного теплового расчета конденсатора лежат-два основных уравнения: уравнение теплового баланса и уравнение теплопередачи. Потери теплоты от корпуса конденсатора в окружающую среду обычно не превышают 1%, поэтому можно считать, что практически вся теплота, выделяющаяся при конденсации пара, передается охлаждающей воде. Тогда уравнение теплового баланса для конденсатора может быть представлено в виде: 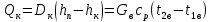 (2.1) (2.1)где Q — количество теплоты, передаваемой от пара к охлаждающей воде в единицу времени (тепловая мощность конденсатора). УРАВНЕНИЕ ТЕПЛОПЕРЕДАЧИ ДЛЯ конденсатора имеет вид: 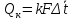 (2.2) (2.2)где k — средний для всей поверхности теплообмена коэффициент теплопередачи конденсатора; F — площадь поверхности теплообмена конденсатора; 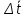 — средняя разность температур между паром и водой для всей поверхности теплообмена конденсатора (среднелогарифмический температурный напор): — средняя разность температур между паром и водой для всей поверхности теплообмена конденсатора (среднелогарифмический температурный напор):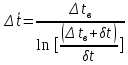 (2.3) (2.3)Учитывая, что система уравнений (2.1) и (2.2) не замкнута, для теплового расчета конденсатора необходимо задаваться рядом параметров теплоносителей и геометрических размеров элементов конденсатора. Методика и расчетная схема зависят от того, какие величины заданы, и от общей постановки задачи. Выбор ряда параметров, определяющих эффективность работы конденсационной установки, должен осуществляться на основе технико-экономического анализа для низкотемпературного комплекса турбины или ПТУ в целом. Основная сложность теплового расчета конденсатора сводится к определению значения среднего для всей поверхности теплообмена коэффициента теплопередачи. Задачей конструкторского расчета конденсатора, как правило, является определение поверхности теплообмена, необходимой для обеспечения заданного давления за турбиной, что осуществляется на основе уравнений (2.1) и (2.2). Согласно уравнению (2.2) 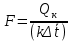 (2.4) (2.4)В качестве исходных данных обычно задаются давление пара в конденсаторе 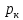 и его расход и его расход 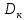 , температура охлаждающей воды на входе в конденсатор , температура охлаждающей воды на входе в конденсатор 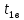 и ее расход и ее расход 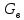 . При этом часто оговаривается ряд параметров и размеров, превышать которые не разрешается. Например, скорость охлаждающей воды в трубках, размеры трубок и др. Могут накладываться отдельные ограничения, связанные с техническими возможностями поставляемого оборудования (например, насосов) и отдельных элементов конденсатора (например, материала и длины трубок). При проведении конструкторского расчета конденсатоpa, при наличии ограничений, чаще всего приходится рассматривать следующие варианты. . При этом часто оговаривается ряд параметров и размеров, превышать которые не разрешается. Например, скорость охлаждающей воды в трубках, размеры трубок и др. Могут накладываться отдельные ограничения, связанные с техническими возможностями поставляемого оборудования (например, насосов) и отдельных элементов конденсатора (например, материала и длины трубок). При проведении конструкторского расчета конденсатоpa, при наличии ограничений, чаще всего приходится рассматривать следующие варианты.1. Тепловой расчет конденсатора по предельной длине трубок и заданному гидравлическому сопротивлению. Сортамент выпускаемых промышленностью трубок, условия их транспортировки, ряд соображений по компоновке турбины и конденсатора позволяют считать длину трубок заданным параметром. Например, в конденсаторах турбин К-300-240, К-500-240, К-220-44, К-500-65 использовались трубки длиной 9 м. Во время проектирования этих конденсаторов такая длина была предельной. Нормативное гидравлическое сопротивление аппарата принималось равным 40 кПа (не более). В последнее время получили широкое распространение трубки длиной 12— 14 м. Изменились и ограничения по гидравлическому сопротивлению конденсатора. 2. Тепловой расчет конденсатора по предельной длине и заданному количеству трубок. Такая постановка вопроса диктуется обычно размерами проема в фундаменте турбины. Это ограничение наиболее часто возникает при проектировании конденсаторов влажно-паровых турбин АЭС, у которых размеры конденсаторов существенно больше, чем у турбин ТЭС той же мощности. При проведении расчета с такими ограничениями используется зависимость для коэффициента заполнения фундаментного проёма 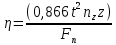 (2.5) (2.5)где t — шаг между трубками конденсатора; 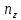 — число трубок в одном ходе охлаждающей воды; z — число ходов воды; — число трубок в одном ходе охлаждающей воды; z — число ходов воды; 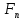 — площадь проема в фундаменте. Тепловой расчет в рассматриваемом варианте проводится для контроля скорости воды в трубках, кратности охлаждения, гидравлического сопротивления аппарата, поскольку поверхность теплообмена при заданных ограничениях (длина, количество трубок) фактически задана. — площадь проема в фундаменте. Тепловой расчет в рассматриваемом варианте проводится для контроля скорости воды в трубках, кратности охлаждения, гидравлического сопротивления аппарата, поскольку поверхность теплообмена при заданных ограничениях (длина, количество трубок) фактически задана.3. Тепловой расчет по минимуму годовых расчетных затрат. Такой вариант расчета проводится при заданных значениях давления в конденсаторе и расхода в нем пара. Составляется так называемая функция цели в виде разности годовых расчетных затрат между рассматриваемым и исходным вариантами. Оптимальные параметры конденсатора определяются по минимуму годовых расчетных затрат с учетом ограничений: допустимая скорость воды, длина трубок и др. Данный вариант расчета аналогичен оптимизации низкотемпературного комплекса турбины и требует большого объема исходных данных по конкретной электростанции. После определения поверхности теплообмена (охлаждения) конденсатора F определяются его основные размеры. Обычно это делается в следующей последовательности. Общее число трубок в конденсаторе 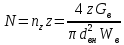 (2.6) (2.6)где 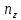 — количество трубок в одном ходе охлаждающей воды; z — число ходов охлаждающей воды; — количество трубок в одном ходе охлаждающей воды; z — число ходов охлаждающей воды; 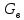 — секундный расход охлаждающей воды, — секундный расход охлаждающей воды, 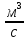 ; ; 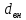 — внутренний диаметр трубки, м; — внутренний диаметр трубки, м; 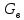 — скорость движения воды в трубках, м/с. — скорость движения воды в трубках, м/с.В практике отечественного конденсаторостроения обычно применяются трубки с внутренним диаметром 22—28 мм, в конденсаторах турбин малой мощности — 14—17 мм. Скорость воды в трубках в большинстве современных конденсаторов на номинальном режиме работы составляет 1,6—2,0 м/с. Допустимые значения скорости составляют 2,5—2,7 м/с для воды без взвеси и 2,0—2,2 м/с при наличии в воде взвеси. Полезная длина трубок конденсатора (без учета толщины трубных досок) определяется зависимостью 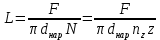 (2.7) (2.7)В инженерной практике, особенно на этапах эскизного проектирования конденсаторов, используется понятие условного диаметра трубной доски конденсатора 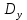 , который можно определить исходя из зависимости , который можно определить исходя из зависимости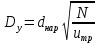 где 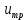 =0,24-0,32 — коэффициент использования трубной доски. =0,24-0,32 — коэффициент использования трубной доски.При проведении поверочного расчета конденсатора обычно задаются следующие параметры: поверхность теплообмена F, температура воды на входе t1в, расходы воды Св и пара DК, число ходов конденсатора по воде z, общее число трубок в конденсаторе N, диаметры трубок; указываются также материал трубок и условный коэффициент чистоты конденсатора. По результатам поверочного расчета обычно строятся зависимости давления (или недогрева воды от температуры насыщения) в конденсаторе от удельной паровой нагрузки аппарата (dK) при различных значениях температуры воды на входе t1в. 2.2. Основы процесса теплопередачи в поверхностном конденсаторе Перенос теплоты от конденсирующего пара к охлаждающей воде через поверхность теплообмена (стенку трубки), разделяющую теплоносители, относится к сложному виду теплообмена. Интенсивность этого процесса характеризуется коэффициентом теплопередачи к, численно равным количеству теплоты, переданной за единицу времени от одного теплоносителя к другому через единицу поверхности при средней разности температур теплоносителей в 1 °С. Рассматривая коэффициент теплопередачи как величину, обратную сумме термических сопротивлений на пути передачи теплоты от пара к воде, запишем 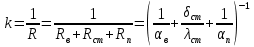 Данное выражение для расчета тонкостенных трубчатых поверхностей конденсатора имеет вид 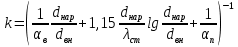 (2.9) (2.9)где 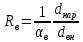 — термическое сопротивление со стороны воды, м2•К/Вт; — термическое сопротивление со стороны воды, м2•К/Вт;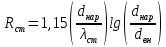 — термическое сопротивление стенки трубки, м2•К/Вт; — термическое сопротивление стенки трубки, м2•К/Вт; 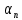 — коэффициент теплоотдачи от пара к стенке трубки, Вт/(м2 • К); — коэффициент теплоотдачи от пара к стенке трубки, Вт/(м2 • К);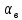 — коэффициент теплоотдачи от стенки трубки к воде, Вт/(м2 • К); dнар , dвн — диаметры трубы наружный и внутренний соответственно, м; — коэффициент теплоотдачи от стенки трубки к воде, Вт/(м2 • К); dнар , dвн — диаметры трубы наружный и внутренний соответственно, м;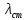 — коэффициент теплопроводности материала стенки трубки, Вт/(м•К). — коэффициент теплопроводности материала стенки трубки, Вт/(м•К).Необходимо иметь в виду, что формула (2.9) не учитывает влияния на коэффициент теплопередачи отложений (загрязнений) с обеих сторон трубок, которые появляются в процессе эксплуатации конденсаторов и оказывают существенное влияние на интенсивность процесса теплопередачи. Учитывая, что процессы теплопередачи как со стороны конденсирующегося пара, так и со стороны однофазного теплоносителя применительно к конденсирующим теплообменным аппаратам. В настоящем разделе остановимся только на особенностях, определящих основы процесса теплопередачи в поверхностном конденсаторе паровой турбины, а также на отдельных зависимостях, положенных в основу методик его теплового расчета. Определение коэффициента теплоотдачи с водяной стороны конденсатора (от стенки трубки к воде) обычно производится по известному уравнению 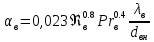 (2.10) (2.10)где 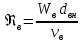 — число Рейнольдса по водяной стороне конденсатора; — число Рейнольдса по водяной стороне конденсатора; 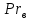 — число Прандтля; — число Прандтля; 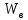 — средняя скорость течения воды в трубках конденсатора, м/с; — средняя скорость течения воды в трубках конденсатора, м/с; 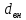 — внутренний диаметр трубок, м; — внутренний диаметр трубок, м; 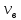 — коэффициент кинематической вязкости воды, м 2 /с; λв— коэффициент теплопроводности воды, Вт/(м • К). — коэффициент кинематической вязкости воды, м 2 /с; λв— коэффициент теплопроводности воды, Вт/(м • К).Здесь за определящую температуру принята средняя температура воды, а определяющий диаметр — внутренний диаметр трубки. Формула (2.10) пригодна для гладких технически чистых трубок в диапазонах чисел Рейнольдса Re=l • 104 - 5 • 106 и Прандтля Рr =0,6-2500. Для расчета коэффициента теплоотдачи при конденсации чистого медленно движущегося пара на одиночной горизонтальной трубке обычно используется полученная Нуссельтом теоретическая зависимость 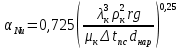 (2.11) (2.11)где 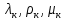 — теплопроводность, плотность и коэффициент динамической вязкости пленки конденсата соответственно, Вт/(м*К), кг/м3 , Н*с/м2 ; r — скрытая теплота парообразования (конденсации), Дж/кг; g — ускорение силы тяжести, м/с2 ; — теплопроводность, плотность и коэффициент динамической вязкости пленки конденсата соответственно, Вт/(м*К), кг/м3 , Н*с/м2 ; r — скрытая теплота парообразования (конденсации), Дж/кг; g — ускорение силы тяжести, м/с2 ; 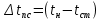 — температурный напор пар—стенка, К; dнар— наружный диаметр трубки, м. — температурный напор пар—стенка, К; dнар— наружный диаметр трубки, м.Формула (2.11) может быть представлена также в безразмерном виде: 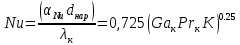 (2.12) (2.12)Где Nu, Gaк, Prк, K — числа Нуссельта, Галилея, Прандтля и фазового перехода. При расчете по формулам (2.11) и (2.12) значения 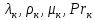 выбираются по средней температуре плёнки выбираются по средней температуре плёнки 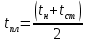 , а r — по температуре насыщения пара. , а r — по температуре насыщения пара.Процесс конденсации неподвижного пара на пучке горизонтальных трубок существенно отличается от конденсации на одиночной трубке. Впервые этот вопрос был также исследован Нуссельтом. В основу расчетной модели было положено пред¬ положение о том, что последовательное стекание конденсата с трубки на трубку влечет за собой увеличение толщины пленки конденсата и соответствующее понижение коэффициента теплоотдачи от пара к нижележащим трубкам. Согласно теории Нуссельта, относительный коэффициент теплоотдачи (по отношению к первой трубке ряда) изменяется по высоте вертикального ряда горизонтально расположенных трубок от 0,7 для второго ряда пучка до 0,4 для двенадцатого. Авторы, исследовавшие теплообмен при пленочной конденсации пара на пучке горизонтальных трубок, не подтверждают данные Нуссельта о таком сильном падении коэффициента теплоотдачи. Визуальные наблюдения за течением конденсатной пленки показывают, что стекание конденсата с трубок происходит дискретно, в виде периодически образующихся отдельных капель, отрыв которых вызывает пульсации (и, следовательно, турбулизацию) конденсатной пленки на трубках. Дискретное стекание конденсата приводит к неоднородности распределения гидравлической нагрузки по длине трубок. Конденсат, падающий сверху на трубку в виде капель и струек, не успевает равномерно распределиться по всей ее длине, а обтекает трубку на сравнительно узких участках (рис. 1). Р 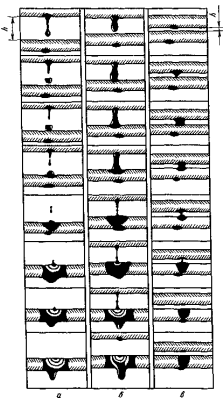 асстояние между отрывным сечением капель на нижней образующей трубки составляет от 50 мм (Reпл=2,5 - 5,0) до 20 мм (Reпл=6,3 - l2,5). Капля в процессе своего формирования стягивает к месту отрыва две-три соседние капли. При Reпл> 14 расстояние между отрывными сечениями становится практически постоянным и составляет примерно 25 мм. При дальнейшем увеличении удельной паровой нагрузки (Reпл) увеличивается частота отрыва капель, превращающихся при Reпл≈30 в прерывистые струйки конденсата. Это позволяет считать, что в зонах трубки, не занятых стекающим сверху конденсатом, процесс конденсации протекает идентично процессу на одиночной трубке и поэтому теплоотдачу в этих зонах можно рассчитывать по формуле Нуссельта. Кроме того при натекании конденсата на нижележащую трубку вместе с ним передается и определенное количество движения, в результате чего негативный эффект заливания конденсатом нижележащей трубки ослабляется ввиду ускорения пленки и ее турбулизации. В ряде работ показано существенное влияние расстояния между соседними горизонтальными трубками в вертикальном ряду на теплообмен при конденсации неподвижного пара. В зависимости от этого расстояния теплообмен может либо ухудшаться, либо интенсифицироваться. Влияние натекания конденсата на теплообмен в пучке горизонтальных трубок может проявиться только тогда, когда вертикальное расстояние между трубками близко к значению капиллярной постоянной (для конденсаторов паровых турбин эти величины различаются на порядок). Анализ экспериментальных исследований по влиянию заливания нижерасположенных трубок горизонтального пучка стекающим сверху конденсатом выявил их различие, что определяется различными условиями проведения исследований. Влияние намокания конденсата на теплообмен в многорядном горизонтальном пучке трубок имеет существенное значение лишь при неподвижном или медленно движущемся паре. асстояние между отрывным сечением капель на нижней образующей трубки составляет от 50 мм (Reпл=2,5 - 5,0) до 20 мм (Reпл=6,3 - l2,5). Капля в процессе своего формирования стягивает к месту отрыва две-три соседние капли. При Reпл> 14 расстояние между отрывными сечениями становится практически постоянным и составляет примерно 25 мм. При дальнейшем увеличении удельной паровой нагрузки (Reпл) увеличивается частота отрыва капель, превращающихся при Reпл≈30 в прерывистые струйки конденсата. Это позволяет считать, что в зонах трубки, не занятых стекающим сверху конденсатом, процесс конденсации протекает идентично процессу на одиночной трубке и поэтому теплоотдачу в этих зонах можно рассчитывать по формуле Нуссельта. Кроме того при натекании конденсата на нижележащую трубку вместе с ним передается и определенное количество движения, в результате чего негативный эффект заливания конденсатом нижележащей трубки ослабляется ввиду ускорения пленки и ее турбулизации. В ряде работ показано существенное влияние расстояния между соседними горизонтальными трубками в вертикальном ряду на теплообмен при конденсации неподвижного пара. В зависимости от этого расстояния теплообмен может либо ухудшаться, либо интенсифицироваться. Влияние натекания конденсата на теплообмен в пучке горизонтальных трубок может проявиться только тогда, когда вертикальное расстояние между трубками близко к значению капиллярной постоянной (для конденсаторов паровых турбин эти величины различаются на порядок). Анализ экспериментальных исследований по влиянию заливания нижерасположенных трубок горизонтального пучка стекающим сверху конденсатом выявил их различие, что определяется различными условиями проведения исследований. Влияние намокания конденсата на теплообмен в многорядном горизонтальном пучке трубок имеет существенное значение лишь при неподвижном или медленно движущемся паре.Рис. 1. Схема течения капель конденсата по трубкам горизонтального пучка Расстояние между соседними трубками (шаг в свету) h составляет: а—24 мм; б — 16 мм; в - 4 мм При достаточно большой скорости пара влияние воздействия парового потока является определяющим. Взаимосвязанное влияние на теплоотдачу при конденсации пара на пучке горизонтальных трубок большого числа факторов не позволяет получить однозначную зависимость относительного коэффициента теплоотдачи от номера трубки, относительного расхода натекающего конденсата и числа рядов по высоте пучка. Подобные зависимости являются, как правило, справедливыми лишь для конкретных условий проведения данных исследований. При конденсации движущегося пара сильно возрастает роль механического взаимодействия паровой и жидкой фаз. В отличие от случая конденсации неподвижного пара, когда касательное напряжение на границе раздела фаз направлено всегда против течения пленки конденсата (оказывает на пленку тормозящее действие), при конденсации движущегося пара касательное напряжение в зависимости от направления парового потока может или подтормаживать, или ускорять течение пленки конденсата и оказывать на теплоотдачу от пара к стенке трубки тем большее влияние, чем выше скорость пара. По данным различных авторов, скорость пара в трубных пучках конденсаторов достигает 150—200 м/с. По мере движения пара через пучок скорость пара уменьшается, что определяется конденсацией части пара на трубках пучка, соответственно уменьшается и теплоотдача от пара к стенке трубки. При прохождении пара через пучок поле его скорости деформируется не только от ряда к ряду трубок, но и по сечению, что определяется совместным влиянием ряда сопутствующих факторов: локальными значениями температурного напора пар—стенка, влиянием стекающего или срываемого паровым потоком конденсата и др. Учитывая эти неопределенности, практически единственным способом определения теплоотдачи движущегося пара в трубных пучках является эксперимент. По опытным данным ВТИ в области давлений пара 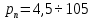 кПа, температурных напорах пар—стенка кПа, температурных напорах пар—стенка 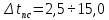 °С и числах Рейнольдса пара перед первым рядом трубок пучка °С и числах Рейнольдса пара перед первым рядом трубок пучка 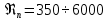 получена обобщенная зависимость получена обобщенная зависимость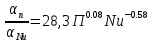 (2.13) (2.13)где 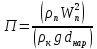 — безразмерное число; — безразмерное число; 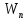 — скорость набегающего потока пара в трубном пучке, м/с; — скорость набегающего потока пара в трубном пучке, м/с;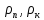 — плотность пара и конденсата, кг/м3 ; g=9,81 м/с2 — ускорение свободного падения; — плотность пара и конденсата, кг/м3 ; g=9,81 м/с2 — ускорение свободного падения; 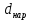 — наружный диаметр трубки, м; — наружный диаметр трубки, м;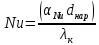 — число Нуссельта для случая конденсации неподвижного пара; — число Нуссельта для случая конденсации неподвижного пара; 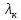 — коэффициент теплопроводности конденсата, Вт/(м*К); — см. формулу (2.11). — коэффициент теплопроводности конденсата, Вт/(м*К); — см. формулу (2.11).Данная зависимость получена для нисходящего направления движения пара в трубном пучке и подтверждена для бокового подвода пара во всем вышеуказанном диапазоне изменения параметров пара. ВТИ при малых скоростях набегающего потока пара 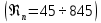 рекомендует зависимость рекомендует зависимость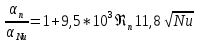 (2.14) (2.14)При конденсации пара в трубных пучках средний коэффициент теплоотдачи помимо других факторов зависит от средней скорости пара в пучке, которая в общем случае определяется выражением 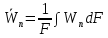 Определение локальных значений 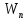 в трубном пучке конденсатора практически невозможно, исключение составляют приближенные методы физико-математического моделирования, поэтому целесообразно учитывать влияние на средний коэффициент теплоотдачи известной скорости пара на входе в трубных пучок в трубном пучке конденсатора практически невозможно, исключение составляют приближенные методы физико-математического моделирования, поэтому целесообразно учитывать влияние на средний коэффициент теплоотдачи известной скорости пара на входе в трубных пучок 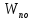 (по горловине конденсатора). В этом случае при (по горловине конденсатора). В этом случае при 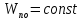 средний коэффициент теплоотдачи средний коэффициент теплоотдачи 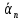 будет зависеть от компоновки трубного пучка конденсатора. будет зависеть от компоновки трубного пучка конденсатора.В качестве параметра, характеризующего компоновку трубного пучка, может использоваться симплекс 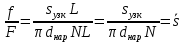 (2.15) (2.15)где f— площадь проходного сечения для пара в узком сечении между трубками по периметру трубного пучка; F — площадь поверхности теплообмена трубного пучка; 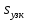 — периметр набегания пара в сечении между трубками по периферии трубного пучка (обычно — периметр набегания пара в сечении между трубками по периферии трубного пучка (обычно 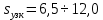 м); N — количество трубок в пучке; L — длина трубок; м); N — количество трубок в пучке; L — длина трубок;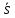 — относительный периметр набегания пара на трубный пучок. — относительный периметр набегания пара на трубный пучок.Таким образом, геометрической характеристикой трубных пучков с различной компоновкой в определенной мере является относительный периметр набегания пара на трубный пучок 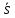 , представляющий собой отношение гидравлического периметра , представляющий собой отношение гидравлического периметра 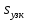 к суммарному периметру поверхности трубок в поперечном сечении пучка к суммарному периметру поверхности трубок в поперечном сечении пучка 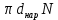 . .Величина 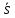 в общем виде учитывает не только изменение скорости пара в трубном пучке при известной скорости пара на входе в общем виде учитывает не только изменение скорости пара в трубном пучке при известной скорости пара на входе 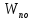 , но и косвенно учитывает влияние стекающего конденсата на теплоотдачу, так как , но и косвенно учитывает влияние стекающего конденсата на теплоотдачу, так как 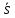 характеризует и глубину трубного пучка конденсатора. характеризует и глубину трубного пучка конденсатора.В многоходовом трубном пучке из-за меньшего температурного напора пар—стенка в верхних ходах конденсатора конденсируется и меньшее количество пара по сравнению с одноходовым пучком. В связи с этим в нижней части пучка поддерживается более высокая скорость пара, происходит менее резкое падение локальных 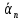 , соответственно возрастает и значение среднего для всего пучка коэффициента теплоотдачи. Учесть перераспределение температурного напора пар—стенка по ходам при известном значении среднего для всего конденсатора температурного напора затруднительно. В связи с этим в уравнение для теплоотдачи , соответственно возрастает и значение среднего для всего пучка коэффициента теплоотдачи. Учесть перераспределение температурного напора пар—стенка по ходам при известном значении среднего для всего конденсатора температурного напора затруднительно. В связи с этим в уравнение для теплоотдачи 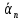 введена дополнительная поправка на число ходов воды, фактически учитывающая изменение температурного напора в отдельных зонах конденсатора. введена дополнительная поправка на число ходов воды, фактически учитывающая изменение температурного напора в отдельных зонах конденсатора.КТЗ по результатам обобщения промышленных испытаний натурных конденсаторов при давлении пара 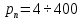 кПа, температурах охлаждающей воды кПа, температурах охлаждающей воды 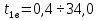 °С, кратности охлаждения m= 15÷300, средней скорости пара в узком сечении на периферии трубного пучка °С, кратности охлаждения m= 15÷300, средней скорости пара в узком сечении на периферии трубного пучка 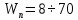 м/с, содержании воздуха в паре на входе в трубный пучок м/с, содержании воздуха в паре на входе в трубный пучок 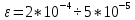 кг/кг получена зависимость кг/кг получена зависимость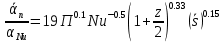 (2.16) (2.16)где 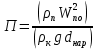 ; ; 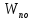 — скорость пара на входе в трубный пучок (по площади горловины конденсатора); z — число ходов воды; значение симплекса — скорость пара на входе в трубный пучок (по площади горловины конденсатора); z — число ходов воды; значение симплекса 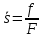 изменялось в диапазоне от 0,004 до 0,020. изменялось в диапазоне от 0,004 до 0,020.Как показано выше, компоновка трубного пучка конденсатора является важным фактором, во многом определяющим пространственную неоднородность распределения скоростей и основных параметров конденсирующегося пара в пучке. Следует отметить, что понятие компоновки включает в себя как собственно конфигурацию трубного пучка, так и компактность, плотность и глубину пучка, а также месторасположение воздухоохладителя. УПИ на основе анализа расчетного исследования и обобщения результатов испытаний большой группы конденсаторов паровых турбин мощностью 100—800 МВт выявлено, что с точки зрения компоновки трубного пучка наиболее сильное влияние на коэффициент теплоотдачи от конденсирующегося пара оказывают параметры 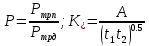 (2.17) (2.17)где Р — относительный периметр трубного пучка; 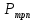 — периметр трубного пучка; — периметр трубного пучка; 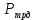 — периметр трубной доски; — периметр трубной доски; 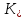 — коэффициент компактности трубного пучка; A — средняя ширина ленты компоновки трубного пучка; — коэффициент компактности трубного пучка; A — средняя ширина ленты компоновки трубного пучка; 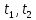 — шаги разбивки труб (см. рис. 3.1). — шаги разбивки труб (см. рис. 3.1).Установлено также, что в сочетании с фактором компоновки на интенсивность теплообмена в трубном пучке конденсатора влияют также скорость пара и начальная температура охлаждающей воды. Влияние этих величин предложено учитывать комплексами 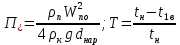 (2.18) (2.18)Где 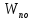 — средняя скорость пара на входе в конденсатор (рассчитывается по площади горловины конденсатора на высоте 1 м над трубным пучком); — средняя скорость пара на входе в конденсатор (рассчитывается по площади горловины конденсатора на высоте 1 м над трубным пучком); 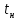 — температура насыщения пара; — температура насыщения пара; 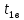 — температура воды на входе в конденсатор. — температура воды на входе в конденсатор.Появление в знаменателе комплекса 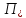 числа 4 вызвано тем, что в качестве определяющей скорости пара в трубном пучке конденсатора принята половина скорости числа 4 вызвано тем, что в качестве определяющей скорости пара в трубном пучке конденсатора принята половина скорости 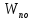 (линейный характер изменения скорости от горловины до патрубка отсоса паровоздушной смеси). (линейный характер изменения скорости от горловины до патрубка отсоса паровоздушной смеси).Зависимость, описывающая влияние компоновки на теплообмен при конденсации пара в пучке, имеет вид: 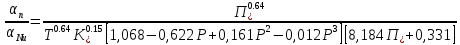 (2.19) (2.19)Данная зависимость получена для практически чистых конденсаторов при допустимых нормами ПТЭ содержаниях в паре воздуха. Наличие в паре воздуха существенно влияет на интенсивность теплообмена при конденсации. Коэффициент теплоотдачи при этом зависит по крайней мере от двух термических сопротивлений — сопротивления пленки конденсата и диффузного сопротивления воздуха. Эти два термических сопротивления взаимосвязаны, что не позволяет решить задачу аналитически. Наиболее удобную зависимость, непосредственно учитывающую содержание воздуха в паре, предложил С. С. Кутателадзе, обобщив опытные данные по конденсации неподвижного пара. Аппроксимация этих данных с погрешностью ±5% позволила получить зависимость 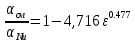 где 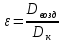 — относительное содержание воздуха в паре, кг/кг. — относительное содержание воздуха в паре, кг/кг.В реальных условиях интенсивность конденсации пара из смеси с воздухом в конденсаторах паровых турбин определяется совместным протеканием процессов тепло- и массообмена, которые находятся в сложной зависимости от большого количества факторов: содержания воздуха в смеси, степени конденсации пара в пучке, скорости пара, удельной паровой нагрузки аппарата, расхода и скорости охлаждающей воды. Определенное влияние оказывают и конструктивные особенности конденсаторов: число ходов воды, эффективность охлаждения паровоздушной смеси в воздухоохладителе, взаимовлияние характеристик конденсатора и воздушного насоса и др. Из-за сложности процесса конденсации пара из паровоздушной смеси в инженерных расчетах аппаратов в настоящее время используются экспериментально полученные обобщенные зависимости. Известен ряд таких зависимостей, в том числе полученных применительно к конденсаторам паровых турбин. Однако эти зависимости, как правило, справедливы лишь для конкретных условий проведения исследований. Известно, что трубки в теплообменных аппаратах, в честности в конденсаторах, в потоке теплоносителя колеблются в режиме автоколебаний с частотой собственных колебаний. Это не может не отражаться на характере течения пленки конденсата, а следовательно, и на теплоотдаче от конденсирующегося пара. Опытами установлено, что в диапазоне частоты колебаний трубки до 50 Гц и амплитуды колебаний до 0,65 мм при удельной паровой нагрузке 40—200 кг/(м2 • ч) вибрирующая трубка при своем движении удерживает конденсатную пленку, перераспределяя ее по периметру трубки, увеличивая тем самым среднюю толщину пленки конденсата. При удельной паровой нагрузке свыше 200 кг/(м2 • ч) вибрирующая трубка турбулизирует пленку конденсата, на поверхности пленки возникают разрывы и происходит срыв отдельных капель с боковых образующих трубки. Анализ экспериментальных данных показал, что в зависимости от удельной паровой нагрузки и параметров вибрации коэффициент теплоотдачи при конденсации пара на вибрирующей трубке может увеличиваться или уменьшаться по сравнению с коэффициентом теплоотдачи при конденсации пара на неподвижной трубке. Результаты опытов обобщены уравнением 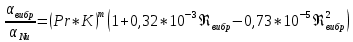 (2.21) (2.21)где 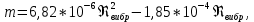 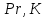 – числа Прандтеля и фазового перехода конденсата соответственно; – числа Прандтеля и фазового перехода конденсата соответственно; 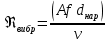 – вибрационное число Рейнольдса; – вибрационное число Рейнольдса; 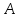 – амплитуда колебаний трубок; – амплитуда колебаний трубок; 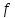 – частота колебаний труб; – частота колебаний труб; 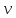 – коэффициент кинематической вязкости конденсата. – коэффициент кинематической вязкости конденсата.Уравнение (2.21) справедливо при 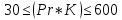 и при и при 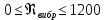 . Определение всех чисел и параметров в этом уравнении производится по температуре насыщения пара. . Определение всех чисел и параметров в этом уравнении производится по температуре насыщения пара.Процесс теплопередачи в поверхностном конденсаторе достаточно хорошо иллюстрируют сложность того, что любое изменение одного из многочисленных режимных факторов (параметров) вызывает перераспределение локальных параметров процесса и интенсивности теплообмена в трубном пучке. Детальный и строгий учет влияния различных факторов на теплообмен в трубных пучках конденсаторов затруднен также из-за сложности определения и описания образующихся в объеме конденсатора трехмерных полей скоростей и других параметров парового потока (паровоздушной смеси). В связи с этим, по мнению большинства специалистов в области исследования, расчета, проектирования и испытаний конденсаторов, наиболее целесообразно проводить тепловые расчеты конденсаторов паровых турбин по апробированным в промышленных условиях эмпирическим зависимостям для среднего по всей поверхности теплообмена коэффициента теплопередачи. Естественно, что эти зависимости должны соответствовать физическим представлениям о процессах, происходящих в конденсаторе, также учитывать все факторы, влияющие на эффективность его работы. |
