задание. 7 кл задание на 2мая. 2. Вычислите Найдите значение выражения 5,51,8 0
 Скачать 115.79 Kb. Скачать 115.79 Kb.
|
|
Домашнее задание «Уровень 1» 1. Найдите значение выражения 2. Вычислите: 3. Найдите значение выражения 5,5 · 1,8 + 0,3. 4. Найдите значение выражения 5. Самолёт, находящийся в полёте, преодолевает 130 метров за каждую секунду. Выразите скорость самолёта в километрах в час. 6. Трамвай движется со скоростью 20 м/с. Какое расстояние он пройдет за время, равное 20 с? Ответ дайте в километрах. 7. Задумали три числа. Первое число составляет 42% суммы всех трёх чисел, второе — 30% этой суммы. Найдите сумму всех трёх чисел, если разность между наибольшим и наименьшим числами равна 77. Запишите решение и ответ. В ответ запишите только число. 8. Фирма проводит обучающие семинары. Стоимость участия в семинаре — 2000 рублей с человека. Группам от организаций предоставляются скидки: от 2 до 5 человек — 3%; более 5 человек — 5%. Сколько рублей должна заплатить организация, направившая на семинар группу из 11 человек? 9. Решите уравнение 10. Решите уравнение: 11. На клетчатой бумаге с размером клетки 1 см x 1 см отмечены точки А, В и С. Найдите расстояние от точки А до середины отрезка ВС. Ответ выразите в сантиметрах.  12. На клетчатой бумаге с размером клетки 1 × 1 нарисован треугольник АВС. Найдите сумму углов АВС и АСВ. Ответ дайте в градусах. 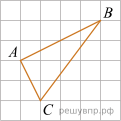 Домашнее задание «Уровень 2» 1. Туристическая фирма организует трехдневные автобусные экскурсии. Стоимость экскурсии для одного человека составляет 3500 р. Группам предоставляются скидки: группе от 3 до 10 человек — 5%, группе более 10 человек — 10%. Сколько заплатит за экскурсию группа из 8 человек? 2. Расходы на одну из статей городского бюджета составляют 12,5%. Выразите эту часть бюджета десятичной дробью. 3. График функции y = −3,6x + b проходит через точку с координатами (7; −3). Найдите коэффициент b. 4. На рисунке изображён график прямой. Напишите формулу, которая задаёт эту прямую. 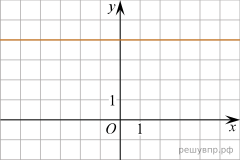 5. Найдите значение выражения 6. В равнобедренном треугольнике ABC с основанием AC угол B равен 120°. Высота треугольника, проведённая из вершины, A равна 8. Найдите длину стороны AC. 7. Биссектриса внешнего угла при вершине В треугольника ABC параллельна стороне АС. Найдите величину угла САВ, если ∠ABC = 36°. Ответ дайте в градусах. 8. Расстояние от пристани А до пристани Б против течения реки катер прошёл за 3 часа, а на обратный путь он затратил на 1 час меньше. Найдите скорость катера в неподвижной воде (собственную скорость), если скорость течения реки 4,6 км/ч. Запишите решение и ответ. 9. Расстояние между пунктами А и В равно 410 км. В 9 часов утра из пункта А в пункт В выехал автобус со скоростью 65 км/ч. В 11 часов утра навстречу ему из пункта В выехал легковой автомобиль со скоростью 75 км/ч. Через некоторое время они встретились. Найдите расстояние от пункта В до места встречи. Запишите решение и ответ. ОТВЕТЫ Уровень 1 1. Ответ: 4 2. Ответ: -1&2|1&-2|-&1&2 3. Ответ: 10,2 4. Ответ: 1,5 5. Ответ: 468 6. Ответ: 0,4 7. Ответ: 550 8. Ответ: 20900 9. Ответ: 4,5 10. Ответ: -6 11. Ответ: 5 12. Ответ: 90 ОТВЕТЫ Уровень 2 1. Туристическая фирма организует трехдневные автобусные экскурсии. Стоимость экскурсии для одного человека составляет 3500 р. Группам предоставляются скидки: группе от 3 до 10 человек — 5%, группе более 10 человек — 10%. Сколько заплатит за экскурсию группа из 8 человек? Решение. Стоимость экскурсии для 8 человек без учёта скидки составляет 3500 · 8 = 28 000 руб. Группе, состоящей из 8 человек, предоставляется скидка 5%: 28 000 · 0,05 = 1400 руб. Таким образом, стоимость экскурсии составит 28 000 − 1400 = 26 600. Ответ: 26 600. 2. Расходы на одну из статей городского бюджета составляют 12,5%. Выразите эту часть бюджета десятичной дробью. Решение. Для того, чтобы представить значение в процентах в виде части от числа, то есть в виде дроби, нужно разделить значение в процентах на 100: 12,5 / 100 = 0,125. Ответ: 0,125. 3. График функции y = −3,6x + b проходит через точку с координатами (7; −3). Найдите коэффициент b. Решение. Подставим точку в уравнение прямой: Ответ: 22,2. 4. Ответ: 5. Найдите значение выражения Решение. Упростим выражение: Найдём значение полученного выражения при Ответ: −29. 6. В равнобедренном треугольнике ABC с основанием AC угол B равен 120°. Высота треугольника, проведённая из вершины, A равна 8. Найдите длину стороны AC. Решение. 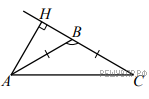 1) Пусть точка H — основание высоты, проведённой из точки A. Из равнобедренного 1) Пусть точка H — основание высоты, проведённой из точки A. Из равнобедренноготреугольника ABC находим: 2) В прямоугольном треугольнике AHC: AC = 2 · AH = 16. Ответ: 16. 7. Биссектриса внешнего угла при вершине В треугольника ABC параллельна стороне АС. Найдите величину угла САВ, если ∠ABC = 36°. Ответ дайте в градусах. Запишите решение и ответ. Решение. 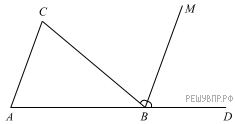 Заметим, что Заметим, что∠CBD = 180° − ∠CBA = 180° − 36° = 144°. Значит, ∠CBM = ∠MBD = 144° : 2 = 72°. Углы САВ и МBD являются соответственными при параллельных прямых АС и ВМ и секущей АВ. Получаем: ∠CAB = ∠MBD = 72°. Ответ: 72°. 8. Расстояние от пристани А до пристани Б против течения реки катер прошёл за 3 часа, а на обратный путь он затратил на 1 час меньше. Найдите скорость катера в неподвижной воде (собственную скорость), если скорость течения реки 4,6 км/ч. Запишите решение и ответ. Решение. Пусть скорость катера в неподвижной воде равна x км/ч. Составим уравнение: откуда Ответ: 23 км/ч. 9. Расстояние между пунктами А и В равно 410 км. В 9 часов утра из пункта А в пункт В выехал автобус со скоростью 65 км/ч. В 11 часов утра навстречу ему из пункта В выехал легковой автомобиль со скоростью 75 км/ч. Через некоторое время они встретились. Найдите расстояние от пункта В до места встречи. Запишите решение и ответ. Решение. Пусть x ч — время, которое двигался до встречи легковой автомобиль, тогда (x + 2) ч — время, которое двигался до встречи автобус. Получаем уравнение: Расстояние, которое проехал до места встречи легковой автомобиль, равно 75 · 2 = 150 (км). Следовательно, они встретились на расстоянии 150 км от пункта В. Ответ: 150 км. |
