конспект урока Перевод чисел из десятичной системы счисления в двоичную и наоборот. Использование приложения Калькулятор 9 кл и. 1 .УРОК ИНТЕГР МАТЕМ И ИНФОРМ КОНКУРСМетодическая разработка уро. 2017г февраль Цели урока
 Скачать 172.5 Kb. Скачать 172.5 Kb.
|
|
Г  КОУ «БАБАЮРТОВСКАЯ СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА-ИНТЕРНАТ№11» КОУ «БАБАЮРТОВСКАЯ СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА-ИНТЕРНАТ№11»  2017г февраль Цели урока: Обучающая Обобщить способ перевода десятичных чисел в двоичную систему счисления, двоичных чисел в десятичную систему счисления, расширить представления учащихся о возможностях приложения Калькулятор. Развивающая Продолжить развитие у учащихся умения самостоятельно делать выводы, обосновывать и высказывать свое мнение. Воспитывающая Продолжить формирование навыков самостоятельной работы на компьютере. Развивать культуру общения, умение работать в паре. Задачи: Повторить способ перевода десятичных чисел в двоичную систему счисления, показать способы перевода двоичных чисел в десятичную систему счисления, научить пользоваться приложением Калькулятор Оборудование: Презентация к данному уроку Карточки Тип урока: Комбинированный урок Знания и навыки учащихся: Уметь переводить целые десятичные числа в двоичную систему счисления и обратно. Умение работать на компьютере с приложением Калькулятор Ход урока Организационный момент. В организационный момент включается проверка домашнего задания. Учитель выясняет, какие задания вызывали затруднения, какие вопросы возникли у учеников. Актуализация опорных знаний учащихся. Фронтальный опрос: • что такое система счисления; • дайте определение понятию «основание системы счисления»; • как перевести число из десятичной системы счисления в двоичную (алгоритм). Система счисления – это принятый способ записи чисел и сопоставления этим записям реальных значений. Все системы счисления можно разделить на два класса: позиционные – количественное значение каждой цифры зависит от ее место положения (позиции) в числе; непозиционные – цифры не меняют своего количественного значения при изменении их положения в числе. Для записи чисел в различных системах счисления используется определенное количество знаков или цифр. Число таких знаков в позиционной системе счисления называется основанием системы счисления. Решим устно: слайды 1.Двоичное число 1010000 в десятичной записи имеет вид: А) 81 Б) 92 В) 80 Г) 78 2.Десятичное число 118 в двоичной записи имеет вид: А) 1110010 Б) 1110011 В) 1110110 Г) 1111001 3.Двоичное число 1001 в десятичной записи имеет вид: А) 9 Б) 8 В) 17 Г) 10 Значит , чтобы перевести числа из двоичной системы в десятичную и наоборот мы должны …. Слайды8-9  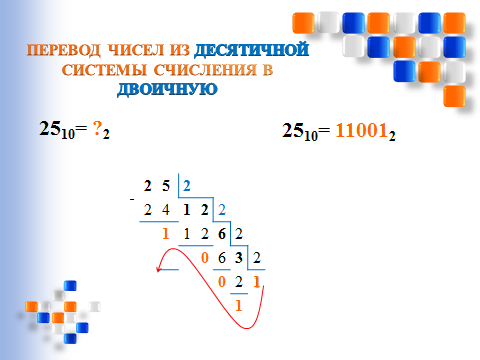 Изучение нового материала. Мы с вами повторили, как переводятся десятичные числа в двоичную систему счисления и наоборот. А сегодня на уроке рассмотрим как переводить целые числа из десятичной системы счисления в двоичную систему счисления и обратно можно с помощью приложения Калькулятор. Сейчас мы будем работать с приложением Калькулятор. Давайте посмотрим, как его найти и как настроить для работы. (Слайд 12-16) Учитель: А теперь, опираясь на новые знания, переведем несколько чисел. А для этого нам понадобится сесть за компьютеры. Давайте вспомним основные правила ТБ при работе на ПК. Прочитайте про себя все внимательно правила и давайте будем следовать им при работе за компьютером. (Учащиеся выполняют практическую работу) Запускаем приложение Калькулятор и выполняем команду (Вид- инженерный). Обратите внимание на группу переключателей, определяющих систему счисления: ·Hex ·Dec · Oct · Bin    Десятичная система счисления Двоичная система счисления Убедимся, что Калькулятор настроен на работу в десятичной системе счисления. С помощью клавиатуры или мыши вводим в поле ввода произвольное число. Активизируем переключатель Bin и в поле ввода видим новое число в двоичной системе счисления. Настроим Калькулятор на работу в двоичной системе счисления. Обратите внимание, какие кнопки и цифровые клавиши нам доступны. Вводим двоичное число и с помощью переключателя Dec переводим его в десятичную систему счисления. Закрепление. Практическая работа в приложении Калькулятор. Нарисуй фигуру Каждой паре выдается карточка, содержащая таблицу с координатами точек, записанными в двоичной системе счисления, и система координат. Для выполнения задания необходимо: а) перевести координаты точек в десятичную систему; б) проверить правильность с помощью программы Калькулятор (этот пункт при желании можно пропустить); в) построить по ним фигуру в координатной плоскости по вариантам: Для выполнения этого задания вам понадобятся не только знания, полученные сегодня на уроке, но и математические знания. Каждому ученику выдается тетрадный лист с нанесенной на нем системой координат (заранее подготавливается учителем) – . Пояснение к заданию: каждая координата точки записана в двоичной системе координат. Вам надо перевести координаты точек в десятичную систему счисления и, применяя знания по математике, построить точки на системе координат, соединить их. Точки одного объекта обозначены одной буквой. I вариант (буква Г) Отметьте и последовательно соедините на координатной плоскости точки, координаты которых приведены в двоичной системе счисления.
Ответ: (5;5), (5;40), (25;40), (25;35), (10;35), (10;5), (5;5). I вариант. Звезда
Ответ: (2;15), (8;16), (11; 22), (14; 16), (20; 15), (16; 10), (18; 4), (11; 7), (4;4), (6;10), (2;15) II вариант. Ракета
Ответ: (8;2), (5;2), (8;10), (8;2), (11;25), (14;21), (14;10), (17;2), (14;2), (14;7), (12;7), (13;2), (9;2), (10;7), (8;7), (8;2). Давайте посмотрим как можно перевести числа в программе EXСEL Слайд 20 Ну а сейчас, ребята, поиграем. Слайд 21 Итог урока. Что нового узнали на уроке? (В виде беседы с классом.) Рефлексия. Вам понравился урок? Чтобы узнать мнение учащихся, учесть их интересы и лучше подготовиться к следующему уроку, можно подготовить два вида смайликов. Учащиеся выбирают тот смайлик, который соответствует их настроению. Слайд22 Дом. задание Вывод: Данный урок сопровождается презентацией. С помощью мультимедийного проектора на экране учащиеся наглядно видят весь теоретический и практический материал данного урока, что повышает результативность и усвояемость данного материала. Данная методическая разработка урока предназначена в помощь учителю, работающему по новому учебно-методическому комплекту по информатике (автор Босова Л.Л., издательство «Бином. Лаборатория знаний»), имеющему гриф «Допущено» Министерства образования РФ. Учебное пособие: Информатика: Учебник /Л.Л. Босова. – 4-е изд., испр. – М.: Бином. Лаборатория знаний, 2006. Информатика: Рабочая тетрадь для 6 класса/ Л.Л. Босова. – М.: Бином. Лаборатория знаний, 2006. Используемая методическая литература: Уроки информатики в 8-9 классах: Методическое пособие/ Л.Л. Босова, А.Ю. Босова. – М.:Бином. Лаборатория знаний, 2004. Занимательные задачи по информатике / Л.Л.Босова, А.Ю.Босова, Ю.Г. Коломенская. – 2-е изд., испр. – М.: Бином. Лаборатория знаний, 2006. |
