Физика. Базовые вопросы и примеры. 20192020 уч год (Лектор Третьякова Лилия Владимировна) комплексные числа
 Скачать 258.5 Kb. Скачать 258.5 Kb.
|
|
ПЕРЕЧЕЬ БАЗОВЫХ ВОПРОСОВ И ЗАДАЧ по высшей математике выносимых на экзамен за II семестр 2019-2020 уч. год (Лектор: Третьякова Лилия Владимировна) КОМПЛЕКСНЫЕ ЧИСЛА Комплексные числа (основные определения). Формы записи комплексного числа. Определение суммы и разности двух комплексных чисел, правила сложения и вычитания. Определение произведения комплексных чисел и правило их умножения во всех формах записи. Формула Муавра возведение комплексного числа в натуральную степень. Определение частного комплексных чисел и правило его нахождения во всех формах записи. Определение корня n-ой степени из комплексного число, и формула нахождений его значений. 1. Представить в тригонометрической и показательной формах комплексные числа:
2. Выполнить действие:
Неопределенный интеграл. 1. Первообразная. Неопределенный интеграл и его геометрический смысл. 2. Основные свойства неопределенного интеграла. 3. Таблица интегралов. 4. Основные методы интегрирования: а) непосредственное интегрирование; б) интегрирование заменой переменных (метод подстановки); в) интегрирование по частям. 5. Понятие правильной и неправильной рациональной дроби, виды простейших дробей I – IV типов. 6. Способ разложения правильной рациональной дроби на сумму простейших. Интегрирование простейших дробей I – II типов. 7. Понятие функции, рационально зависящей от тригонометрических. Универсальная подстановка. 8. Интегрирование простейших алгебраических иррациональностей. Уметь решать следующие примеры 1. Непосредственное интегрирование:
2. Интегрирование заменой переменной:
3. Интегрирование по частям:
4. Интегрирование дробно рациональных функций:
5. Интегрирование функций, рационально зависящих от тригонометрических:
6. Интегрирование простейших алгебраических иррациональностей:
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ. 1. Основные понятия фнп. Область и ее граница. 2. Определение функции двух переменных, ее график, способы задания. 3. Частные и полный дифференциал. 4. Производная сложной функции. 5. Дифференцирование неявных функций. 6. Касательная плоскость и нормаль к поверхности. Уметь решать следующие примеры 1. Найти частные производные первого порядка функций по всем переменным: а) 2. Найти частные производные второго порядка по переменной х: а) 3. Найти полный дифференциал функций: а) 4. Найти производные сложных функций: а) б) Определенный интеграл Определенный интеграл, как предел интегральной суммы. Геометрический смысл определенного интеграла. Площадь криволинейной трапеции. Связь неопределенного интеграла с определенным. Формула Ньютона-Лейбница. Основные свойства определенного интеграла. Методы вычисления о.и. (формулы замены переменной и интегрирования по частям в определенном интеграле). Интегрирование четных и нечетных функций на отрезке, симметричном относительно нуля. Уметь решать следующие примеры 1. Вычислить:
2. Исследовать сходимость несобственных интегралов (по определению):
3. Вычислить площадь плоских фигур, ограниченных линиями: а) б) в) первой аркой циклоиды 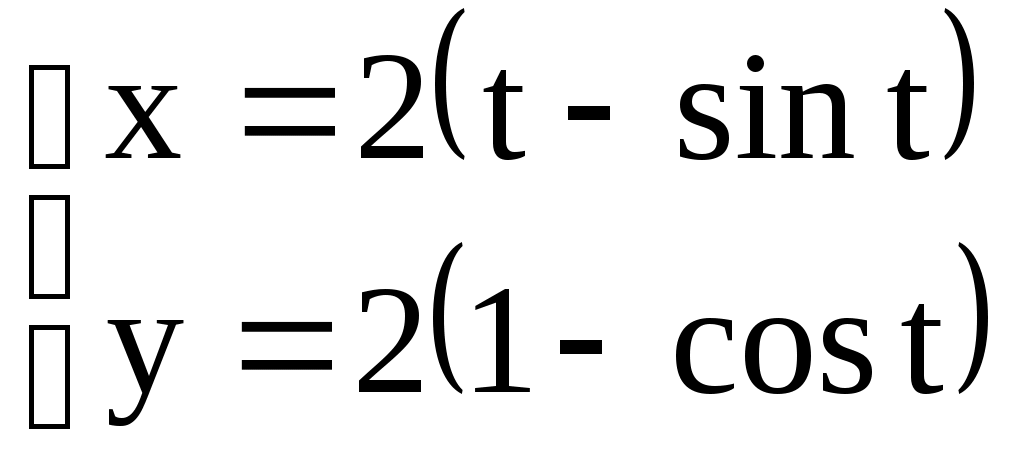 и осью ОХ. и осью ОХ. г) эллипсом д) кардиоидой ж) четырех лепестковой розой 4. Найти длины дуг кривых: а) параболы б) полукубической параболы в) астроиды 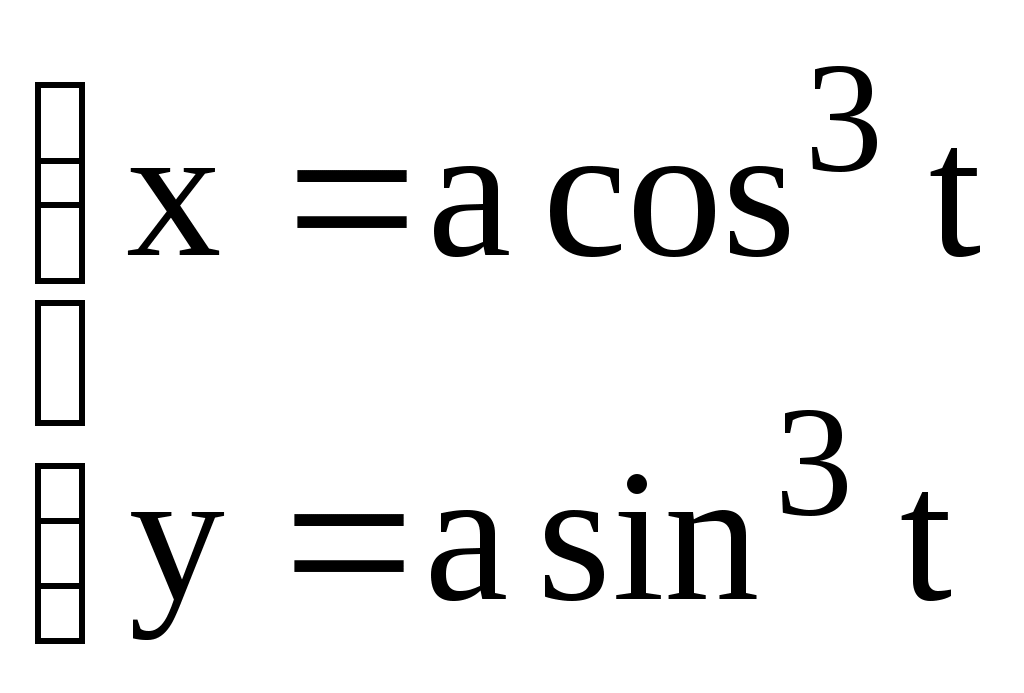 ; г) ; г) 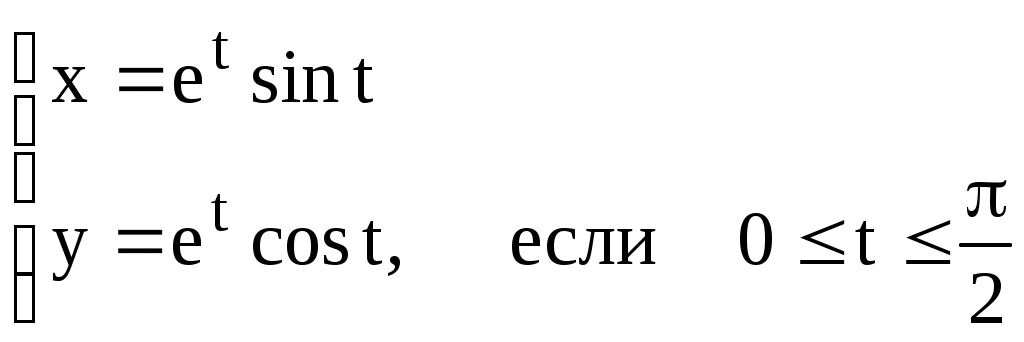 д) кардиоиды ж) первого витка спирали Архимеда: 5. Вычислить объем тела, полученного вращением. а) вокруг оси ОХ фигуры, ограниченной линиями б) вокруг оси ОУ фигуры, ограниченной линиями в) вокруг оси ОХ фигуры, ограниченной линиями Дифференциальные уравнения первого порядка. Определения дифференциального уравнения, его порядка, решения. Определения общего и частного решений д.у. I-го порядка. Определение д.у. с разделяющимися переменными и метод его решения. Определение линейного д.у. и метод его решения. Уметь решать следующие примеры С разделяющимися переменными. а) в) Линейные, уравнения Бернулли: а) Дифференциальные уравнения 2-го и высших порядков. Определения общего и частного решений д.у. 2-го порядка и высших. Линейные однородные и неоднородные д.у. 2-го и высших порядков. Теорема о частных решениях линейного однородного д.у. 2-го порядка. Фундаментальная система решений ЛОДУ 2-го порядка и ее свойства. Теорема о структуре общего решения ЛОДУ 2-го и высших порядков. Теорема о частном решении ЛОДУ 2-го порядков. Решение линейных однородных д.у. 2-го порядка с постоянным коэффициентами в случае: а) действительных различных корней; б) действительных кратных корней; в) комплексно-сопряженных корней. Метод решения ЛНДУ 2-го и высших порядков с постоянными коэффициентами и специальной правой частью вида: а) б) Уметь решать следующие примеры Линейные однородные д.у. с постоянными коэффициентами: а) в) Линейные неоднородные д.у. с постоянными коэффициентами и специальной правой частью: а) г) |

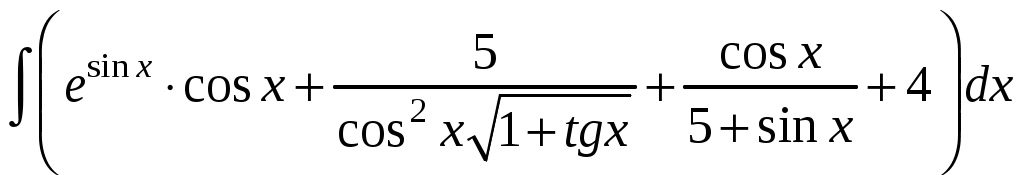 ;
;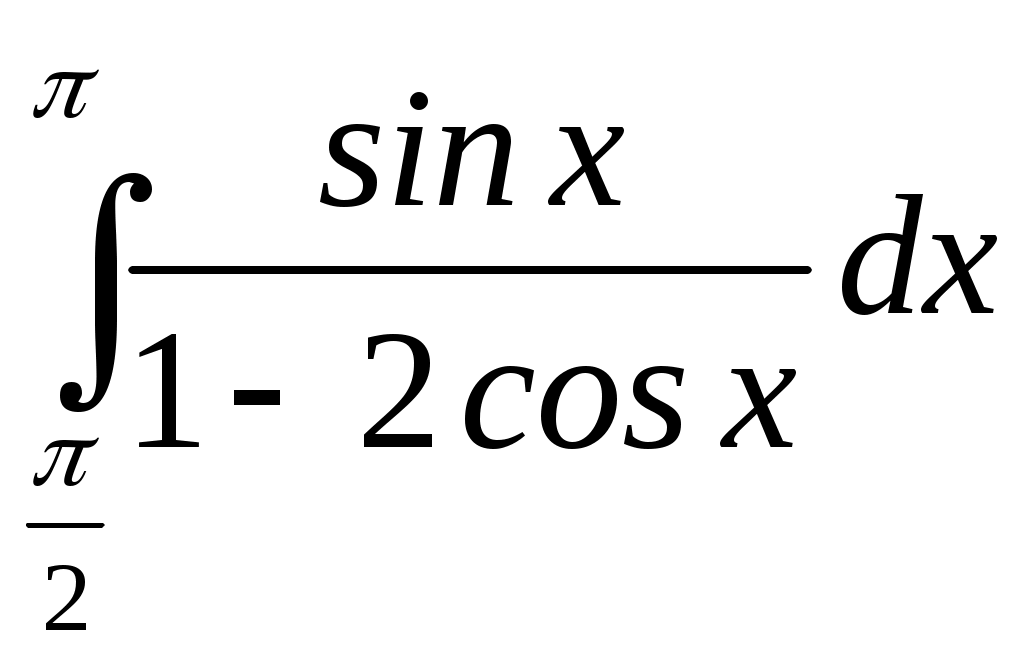 ;
;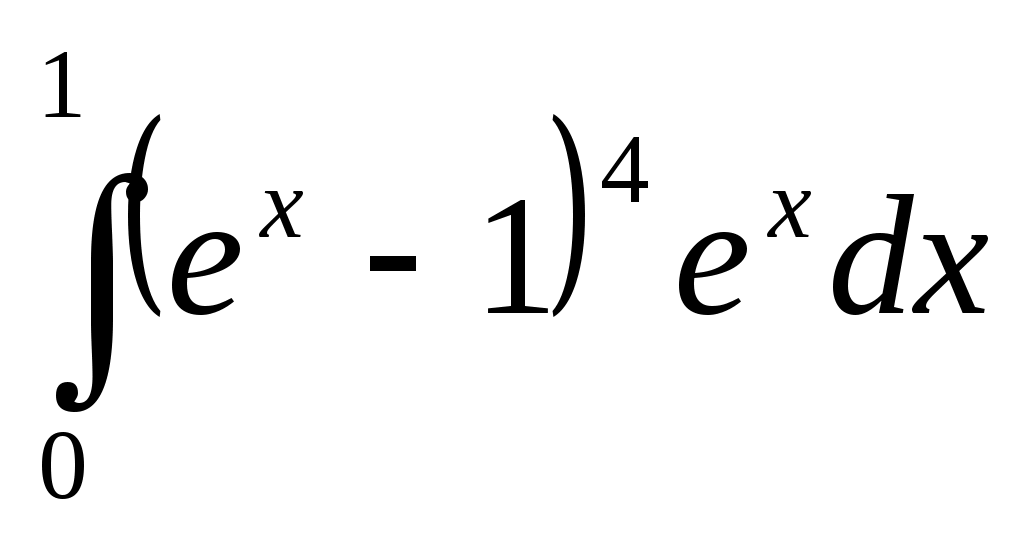 .
.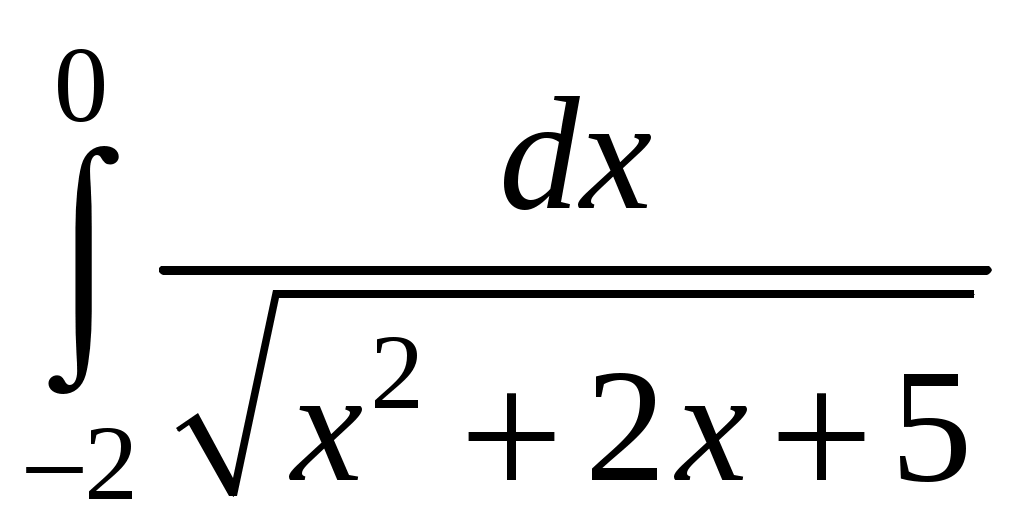 .
.