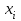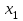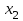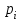Матем 2 технари. Шпаргалка (7). 2i. Найдите частную производную первого порядка функции 2у
 Скачать 269.91 Kb. Скачать 269.91 Kb.
|
|
1. Даны комплексные числа z1 = 2 + 2i, z2 = 1-i. Вычислить 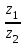 .<variant>2i. .<variant>2i.2.Найдите частную производную первого порядка 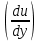 функции функции 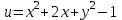 <variant>2у <variant>2у 3. Вероятность исправной работы агрегата 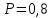 . Найти вероятность того, что он выйдет из строя. <variant>0,2 . Найти вероятность того, что он выйдет из строя. <variant>0,2 4. Вероятность наступления события А 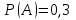 ; вероятность наступления события В ; вероятность наступления события В 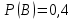 . Найти вероятность того, что в результате испытаний наступят оба события. <variant>0,12 . Найти вероятность того, что в результате испытаний наступят оба события. <variant>0,12 5. Вероятность наступления события А 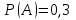 ; вероятность наступления события В ; вероятность наступления события В 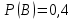 . Найти вероятность того, что в результате испытаний не наступит ни одного события. <variant>0,42 . Найти вероятность того, что в результате испытаний не наступит ни одного события. <variant>0,42
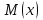 по данному закону распределения: <variant> по данному закону распределения: <variant>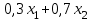 7. Вычислить число сочетаний 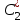 . <variant>2 . <variant>2 8. Сумма вероятностей полной группы событий равна…. <variant>1 9. Даны комплексные числа z1=1+2i z2=3-4i. Найти сумму чисел. <variant>4-2i 10. Дисперсия непрерывной случайной величины 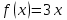 , заданной в интервале , заданной в интервале 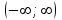 вычисляется по формуле: <variant> вычисляется по формуле: <variant>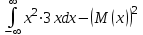 11. Замена 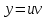 применяется при решении дифференциальных уравнений I порядка: <variant>линейных применяется при решении дифференциальных уравнений I порядка: <variant>линейных 12.Решить дифференциальное уравнение: 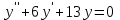 . . <variant> 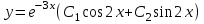 13.для исследования сходимости ряда 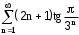 рационально использовать признак: <variant>Даламбера рационально использовать признак: <variant>Даламбера 14. Определить тип дифференциального уравнения I-го порядка y/ + y = y2 <variant>с разделяющимися переменными; 15. Исследовать ряд на сходимость, с указанием признака: 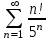 <variant>расходится, Даламбера 16. Записать разложение функции 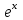 : <variant> : <variant>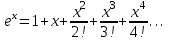 17. Дифференциальное уравнение 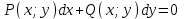 называется уравнением…, если… называется уравнением…, если…<variant>в полных дифференциалах, 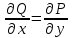 . .18. Если событие невозможно, то вероятность его появления равна…… <variant>0 19.Сколькими способами можно поставить 3 книги на полке. <variant>3! 20. Число событий, благоприятствующих событию А равно 3, число всевозможных 4. Найти вероятность наступления события А. <variant>3/4 21 Если интегральная функция 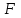 распределения непрерывной случайной величины, заданная в некотором интервале распределения непрерывной случайной величины, заданная в некотором интервале 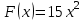 , то соответствующая ей дифференциальная функция , то соответствующая ей дифференциальная функция 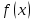 равна <variant>30х равна <variant>30х 22. Если математическое ожидание 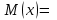 5 5 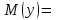 2, то 2, то 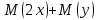 равно…<variant>12 равно…<variant>12 23. Замена 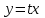 ; ; 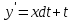 применяется при решении дифференциальных уравнений I порядка: <variant>однородных применяется при решении дифференциальных уравнений I порядка: <variant>однородных24. Определить тип дифференциального уравнения I-го порядка 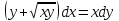 <variant>однородное дифференциальное уравнение; <variant>однородное дифференциальное уравнение;25.Указать способ понижения порядка дифференциального уравнения y///x2 = x + 1 <variant>разрешив уравнение относительно старшей производной, интегрировать 26. Записать структуру частного решения линейного неоднородного дифференциального уравнения: 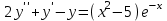 <variant> <variant>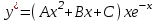 27.Формула Пуассона при 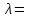 9 имеет вид: <variant> 9 имеет вид: <variant>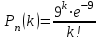 28. Исследовать ряд на сходимость, с указанием признака: 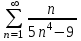 <variant> сходится, сравнения . 29. Если предел отношения Un к Vn равен отличной от нуля константе, то оба ряда…. <variant>ведут себя одинаково 30. Записать разложение функции 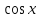 в ряд: <variant> в ряд: <variant>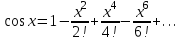 31. Найти М(х) для случайной величины х, заданной : <variant>2,4
32. Если появление события совершенно достоверно, то его вероятность равна …… <variant>1 33.Сколькими способами можно поставить 4 книги на полке. <variant>4! 34.Число событий, благоприятствующих событию А равно 2, число всевозможных 3. Найти вероятность наступления события А. <variant> 2/3 35. Даны комплексные числа z1=3+2i, z2=3-4i. Найти 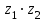 .<variant>17-6i; 36. Найти .<variant>17-6i; 36. Найти 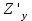 , функции , функции 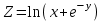 <variant> <variant>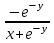 37. Вероятность исправной работы агрегата 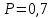 . Найти вероятность того, что он выйдет из строя. <variant>0,3 . Найти вероятность того, что он выйдет из строя. <variant>0,3 38. Вероятность наступления события А 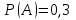 ; вероятность наступления события В ; вероятность наступления события В 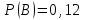 . Найти вероятность того, что в результате испытаний наступят оба события. <variant>0,036 . Найти вероятность того, что в результате испытаний наступят оба события. <variant>0,036 39. Вероятность наступления события А 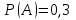 ; вероятность наступления события В ; вероятность наступления события В 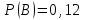 . Найти вероятность того, что в результате испытаний не наступит ни одного события. <variant>0,616 . Найти вероятность того, что в результате испытаний не наступит ни одного события. <variant>0,616
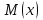 по данному закону распределения: по данному закону распределения: <variant> 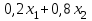 41. Вычислить число сочетаний 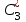 . <variant>3 . <variant>3 42. Вероятность совместного появления двух независимых событий А и В, находится по формуле: <variant>Р(АВ) = Р(А)Р(В) 43. Даны комплексные числа 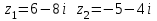 . Найти . Найти 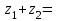 <variant> <variant>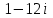 44. Дисперсия непрерывной случайной величины 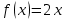 , заданной в интервале , заданной в интервале 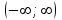 вычисляется по формуле: <variant> вычисляется по формуле: <variant>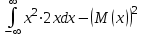 45. Определить тип дифференциального уравнения I-го порядка y/ - xy2 = 2xy <variant>с разделяющимися переменными; 46. Указать способ понижения порядка дифференциального уравнения xy// = sin x <variant>разрешив уравнение относительно старшей производной, интегрировать 47. Записать общее решение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами 2y// – 3y/ + y = 0 <variant>y = C1ex + C2ex/2; 48. Даны комплексные числа 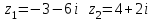 . Найти . Найти 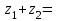 <variant> <variant>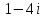 49. для исследования сходимости ряда 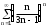 рационально использовать признак: <variant>Радикальный Коши рационально использовать признак: <variant>Радикальный Коши 50. Замена 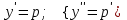 применяется при решении дифференциальных уравнений вида: <variant> применяется при решении дифференциальных уравнений вида: <variant>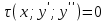 51. Решить дифференциальное уравнение: 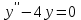 . . <variant> <variant>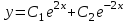 52. Исследовать на сходимость знакопеременный ряд: 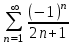 <variant>сходится условно 53.Записать в общем виде ряд Маклорена <variant> 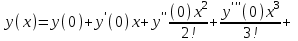 … …54.Если для уравнения 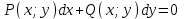 выполнено условие выполнено условие 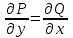 , то: , то:<variant> это уравнение в полных дифференциалах 55. Два события, вероятность появления одного из которых зависит от наступления (или не наступления) другого, называютс<variant>зависимыми 56. Сколькими способами можно поставить 5 книги на полке. <variant>5! 57. Число событий, благоприятствующих событию А равно 4, число всевозможных 5. Найти вероятность наступления события А.<variant>4/5 58. Даны комплексные числа z1 = 6-3i, z2 = 3i. Найти 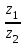 .<variant>1+2i; .<variant>1+2i; 59. Вероятность исправной работы агрегата 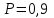 . Найти вероятность того, что он выйдет из строя. <variant>0,1 . Найти вероятность того, что он выйдет из строя. <variant>0,1 60.Вероятность наступления события А 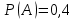 ; вероятность наступления события В ; вероятность наступления события В 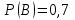 . Найти вероятность того, что в результате испытаний наступят оба события. <variant>0,28 . Найти вероятность того, что в результате испытаний наступят оба события. <variant>0,28 61. Записать 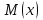 по данному закону распределения: по данному закону распределения:
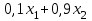 62. Вычислить число сочетаний 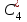 . .<variant>4 63.Вероятность совместного появления двух зависимых событий, вычисляется по формуле: <variant>Р(АВ) = Р(А)РА(В) 64. Если математическое ожидание 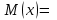 6 6 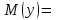 1, то 1, то 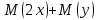 равно… равно…<variant>13 65. Указать формулу полной вероятности: <variant> 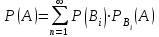 66. Определить тип дифференциального уравнения I-го порядка y/ = 5x – y <variant>с разделяющимися переменными; 67. Замена 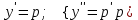 применяется при решении дифференциальных уравнений вида: <variant> применяется при решении дифференциальных уравнений вида: <variant>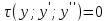 68.Решить дифференциальное уравнение: 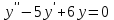 . <variant> . <variant>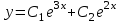 69. Исследовать на сходимость знакопеременный ряд: 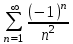 <variant>сходится абсолютно 70.Даны комплексные числа 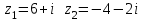 . Найти . Найти 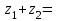 <variant> <variant> 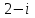 71. Исследовать ряд на сходимость, с указанием признака: 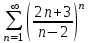 <variant>расходится, Коши 72. Записать в общем виде ряд Тейлера: <variant> 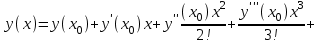 … …73.Уравнение 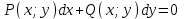 является дифференциальным уравнением в полных дифференциалах, если: <variant> является дифференциальным уравнением в полных дифференциалах, если: <variant>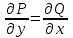 74. Вероятность совместного появления двух независимых событий А и В, равна …… <variant>сумме вероятностей этих событий 75. Сколькими способами можно поставить 6 книги на полке.<variant>6! 76.Число событий, благоприятствующих событию А равно 2, число всевозможных 7. Найти вероятность наступления события А. <variant>2/7 77. Даны комплексные числа z1 = 3 – 5i, z2 = 4 + 2i. Найти z1·z2. 78. Найдите частную производную первого порядка  функции функции  : <variant>–2х : <variant>–2х 79.Вероятность исправной работы агрегата  . Найти вероятность того, что он выйдет из строя. <variant>0,6 . Найти вероятность того, что он выйдет из строя. <variant>0,6 80 Вероятность наступления события А  ; вероятность наступления события В ; вероятность наступления события В 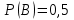 . Найти вероятность того, что в результате испытаний наступят оба события. <variant>0,25 . Найти вероятность того, что в результате испытаний наступят оба события. <variant>0,25
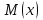 по данному закону распределения: по данному закону распределения: <variant> 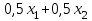 82. Вычислить число сочетаний 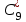 .<variant>9 .<variant>9 83. Если некоторое событие возможно, но его появление не абсолютно достоверно, то вероятность его появления будет число, заключенное между: <variant>0 и 1 84. Указать формулу Бейеса: <variant>  85. Если для ряда  с положительными членами существует с положительными членами существует  , то этот ряд сходится при , то этот ряд сходится при и расходится при и расходится при 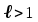 . Это: . Это: <variant>радикальный признак Коши; 86.Уравнение вида y’+P(x)y=Q(x), где P(x) и Q(x)–непрерывные функции х, называется <variant>линейным; 87. Данный ряд 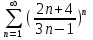 исследуем на сходимость по признаку: <variant>Коши исследуем на сходимость по признаку: <variant>Коши 88. Записать общее решение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами y// – 2y/ + 10y = 0 <variant>y = ex (C1 cos3x + C2sin3x); 89. для исследования сходимости ряда 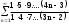 рационально использовать признак: <variant>Даламбера рационально использовать признак: <variant>Даламбера 90. Два события, появление одного из которых исключает появление другого в одном и том же испытании, называются: <variant>несовместными 91. Вероятность наступления события А 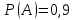 ; вероятность наступления события В ; вероятность наступления события В 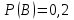 . Найти вероятность того, что в результате испытаний наступят оба события. <variant>0,18 . Найти вероятность того, что в результате испытаний наступят оба события. <variant>0,18 92. Найти сопряженное число к числу 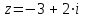 <variant> <variant> 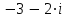
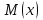 по данному закону распределения: <variant> по данному закону распределения: <variant>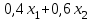 94. Вычислить число сочетаний 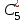 . <variant>5 . <variant>5 95. Вероятность появления одного из двух несовместимых событий, безразлично какого, определяется по формуле: <variant>Р(А + В) = Р(А) + Р(В) 96.Если интегральная функция 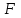 распределения непрерывной случайной величины заданная в некотором интервале распределения непрерывной случайной величины заданная в некотором интервале 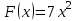 , то соответствующая ей дифференциальная функция , то соответствующая ей дифференциальная функция 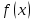 равна <variant>14х равна <variant>14х 97.Если математическое ожидание 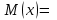 8 8 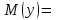 2, то 2, то 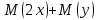 равно… равно…<variant>18 98Указать формулу теоремы сложения вероятностей для двух событий: <variant> 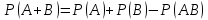 99.Если для ряда 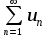 с положительными членами таков, что существует с положительными членами таков, что существует 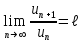 , то при , то при 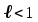 ряд сходится, а при ряд сходится, а при 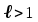 расходится. Это: расходится. Это:<variant>признак Даламбера; . 100.Уравнение вида a0y”+ a1y’+ a2y=0, где a0, a1, a2 –постоянные, называется. <variant>линейным однородным II порядка; 101. Дана функция 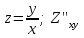 найти производную. <variant> найти производную. <variant>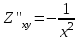 102. Дана функция 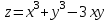 , найти производные , найти производные 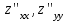 <variant 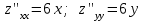 103. Разложить в ряд Тейлора по степеням х, функцию Sin2x: <variant 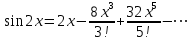 104. Разложить в ряд Тейлора функцию е3х по степеням х: <variant 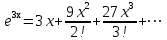 105. В показательной форме комплексное число 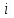 имеет вид: <variant> имеет вид: <variant>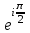 106. Если математическое ожидание 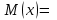 2; 2; 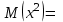 10, то дисперсия 10, то дисперсия 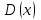 равна <variant>6 равна <variant>6107 Исследовать на сходимость знакопеременный ряд: 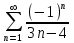 <variant>сходится условно 108. Найти 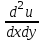 для функции для функции 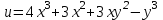 <variant>6у <variant>6у109. Найти область сходимости ряда: 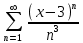 <variant> [2;4] <variant> [2;4]110. Найти 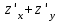 в М0(1;1), если в М0(1;1), если 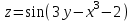 <variant>0 <variant>0111. Известно, что математическое ожидание 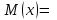 5; 5; 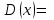 61, найти 61, найти 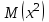 <variant>86 112. В студенческой группе 15 девушек и 10 юношей. Случайным образом (по жребию) выбирают одного. Найти вероятность того, что будет отобран юноша. <variant>3/5 113. Исследовать на сходимость знакопеременный ряд: 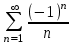 . .<variant> сходится условно, Лейбница 114. Если математическое ожидание 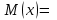 3 3 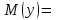 2, то 2, то 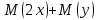 равно равно<variant> 8 115. Решить дифференциальное уравнение: 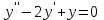 . <variant> . <variant>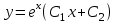 116. Исследовать на сходимость знакопеременный ряд: 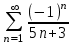 <variant>сходится условно, Лейбница 117. Найти 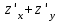 в М0(1;1), если в М0(1;1), если 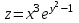 <variant>5 <variant>5118. Найти область сходимости ряда: 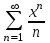 <variant>[-1;1) <variant>[-1;1)119. Найти область сходимости ряда: 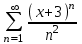 <variant>[-4;-2] <variant>[-4;-2]120. Найти 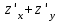 в М0(1;1), если в М0(1;1), если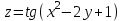 <variant>0 <variant>0121. Известно, что математическое ожидание 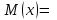 3; 3; 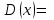 12, найти 12, найти 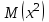 <variant>21 122. Исследовать ряд на сходимость, с указанием признака: 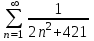 <variant>сходится, сравнения 123. Если дисперсия 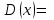 4, то 4, то 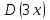 равна <variant>36 равна <variant>36124. Найти область сходимости ряда 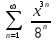 . <variant>(-2;2) . <variant>(-2;2)125. Найти частные производные функции 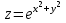 <variant>z'x= <variant>z'x=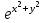 2x, z'у= 2x, z'у=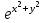 2у 2у126. Найти область сходимости ряда 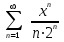 . <variant>[-2;2) . <variant>[-2;2)127. Известно, что математическое ожидание 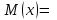 6; 6; 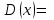 3, найти 3, найти 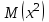 <variant>39 <variant>39128. В урне 10 белых , 15 черных и 25 красных шаров. Вынули один шар. Найти вероятность того, что вынутый шар белый или красный. <variant>0,7 129. Абитуриент сдает два вступительных экзамена: по математике и по физике. Найти вероятность того, что абитуриент получит только одну пятерку, если вероятность получения пятерки по математике равна 0,8, а по физике – 0,6. <variant>0,44 130. Найти для функции 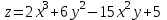 значение выражения значение выражения 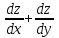 в точке А(1,-1): <variant>9 в точке А(1,-1): <variant>9131. Вероятность того, что образец бетона выдержит нормативную нагрузку, равна 0,9.Найти вероятность того, что из 7 образцов испытание выдержат ровно5.(ответ округлить до 0,001) <variant>0,124 132. Записать общее решение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами 4y// + 4y/ + y = 0 <variant> 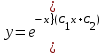 133. Вероятность появления события А равна 0,4. Какова вероятность того, что в 4 испытаниях событие А появится ровно 3 раза? <variant>0,1536 134. Вероятность появления события А равна 0,4. Какова вероятность того, что в 4 испытаниях событие А появится ровно 2 раза? <variant>0,3456 135.Найти область сходимости ряда: 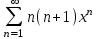 <variant> <variant>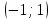 136. Записать общее решение линейного однородного уравнения второго порядка с постоянными коэффициентами y// + 8y/ + 16y = 0 137. В студенческой группе 15 девушек и 10 юношей. Случайным образом (по жребию) выбирают одного. Найти вероятность того, что будет отобрана девушка. <variant>0,4 138. Найти область сходимости ряда: 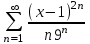 <variant>(-2;4) <variant>(-2;4)139. 3Исследовать на сходимость ряд с положительными членами 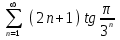 . <variant>сходится . <variant>сходится140.Решением, какого дифференциального уравнения является функция y = 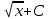 <variant> <variant>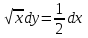 |