Механика колебния волны. 3. 14. Тело брошено под углом к горизонту. По заданным параметрам движения материальной точки определить все недостающие параметры по таблице.
 Скачать 126.5 Kb.
|
|
3.14. Тело брошено под углом α к горизонту. По заданным параметрам движения материальной точки определить все недостающие параметры по таблице. Решение задачи сопроводить чертежом, на котором показать все векторные величины. Обозначения: α – угол между направлением начальной скорости  и осью  ,  и  – проекции вектора скорости на оси и  для момента времени  ,  и  – проекции вектора перемещения на оси и для момента времени ,  - нормальное ускорение и  - тангенциальное ускорение в момент времени ,  – радиус кривизны траектории в момент времени ,  – полное время движения,  – дальность полета,  – максимальная высота полета. В расчетах ускорение свободного падения можно принять равным  .Дано: ,
Решение: Все расчетные формулы для оси ОХ берутся как для равномерного движения, а на ось ОУ как для равноускоренного движения с ускорением свободного падения. Скорости тела в заданный момент времени по осям:  ,Откуда начальная скорость:  .Путь, пройденный точкой к заданному моменту времени:  ,Откуда заданное время:  .Скорости тела в заданный момент времени по осям:  ,Полная скорость точки в этот момент:  ,Путь, пройденный точкой к заданному моменту времени:  .Для удобства введем угол φ. Из рисунка видно, что:  и .Значение нормального ускорения:  ,Откуда выразим радиус кривизны траектории:  .Полное смещение точки по OX и OY соответственно:  ,  . |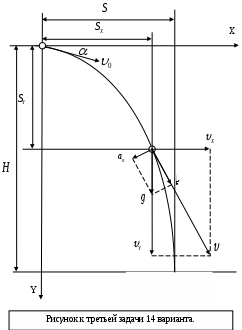
