пися. 1номер. 3 Исследовать функцию на выпуклость в функцию
 Скачать 177.06 Kb. Скачать 177.06 Kb.
|
|
3  ) Исследовать функцию на выпуклость в ) Исследовать функцию на выпуклость в 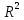 функцию функцию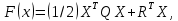 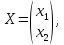 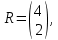 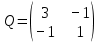 Решить задачу 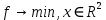 Градиентным методом, выбирая в качестве начального приблежения произвольную точку из 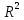 . Шаг в градиентном методе следует выбирать из условии монотонности функции. Полученное решение уточните с помощью метода Ньютона. . Шаг в градиентном методе следует выбирать из условии монотонности функции. Полученное решение уточните с помощью метода Ньютона.3. Данная функция выпукла. Действительно, 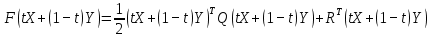 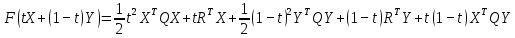 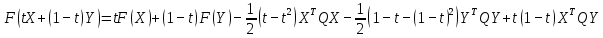 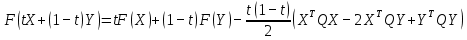 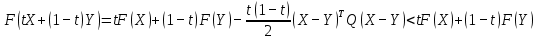 так как матрица Q положительно определена по критерию Сильвестра. Координаты градиента функции: 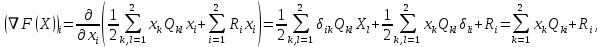 то есть 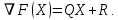 В качестве начального приближения выберем 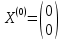 . . В этом случае 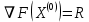 и первый шаг метода наискорейшего спуска и первый шаг метода наискорейшего спуска 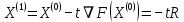 , ,где параметр выбирается исходя из условия 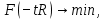 то есть, то есть, 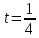 , так как , так как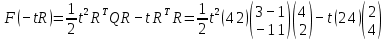 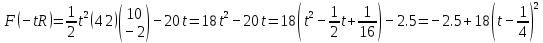 Получили 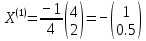 Далее 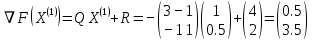 и второй шаг метода наискорейшего спуска: и второй шаг метода наискорейшего спуска: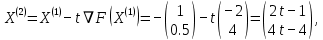 где параметр выбирается исходя из условия 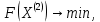 то есть то есть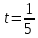 , так как , так как 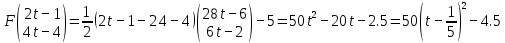 Таким образом, 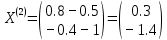 Далее 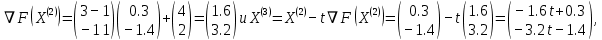 где параметр выбирается исходя из условия 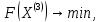 то есть, то есть, 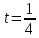 , так как , так как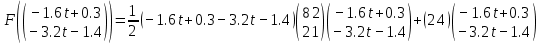 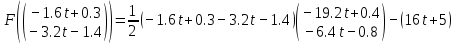 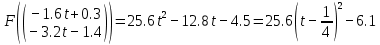 Таким образом, 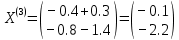 Далее 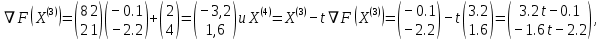 где параметр выбирается исходя из условия 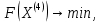 то есть, то есть, 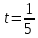 , так как , так как 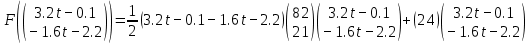 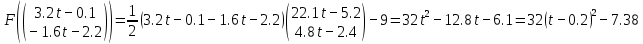 Таким образом, 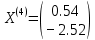 Далее 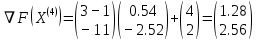 Уточнение методом Ньютона. Найдем гессиан функции: 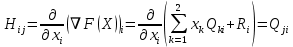 Таким образом, 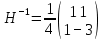 / /Итерация метода Ньютона: 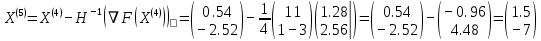 Это – точное решение, так как 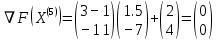 . . |
