Консультация. 3. Метод наименьших квадратов (мнк)
 Скачать 43.05 Kb. Скачать 43.05 Kb.
|
|
3. Метод наименьших квадратов (МНК). Математический метод, позволяющий найти оценки параметров модели путем минимизации суммы квадратов отклонений 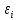 . Он позволяет разместить линию, описывающую облако точек наблюдений, наилучшим образом. . Он позволяет разместить линию, описывающую облако точек наблюдений, наилучшим образом.7. Теорема Гаусса-Маркова. Предпосылки регрессионного анализа Мат. Ожидание случайного члена должно быть равно нулю: M  Дисперсия случайного члена должна быть постоянной для всех наблюдений D  Случайные члены должны быть статистически независимы между собой: cov  Ошибки регрессии нормально распределены: 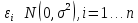 Случайные отклонения должны быть статистически независимы от объясняющих переменных Если эти условия регрессионного анализа выполняются, то оценки, сделанные с помощью МНК, являются наилучшими линейными несмещенными оценками, то есть обладают свойствами несмещенности, эффективности(наименьшая дисперсия), состоятельности(при достаточно большом n оценки близки к параметрам) 34. Тест Чоу Используется для проверки однородных двух выборок, а именно проверяется нулевая гипотеза, что две выборки описываются одним и тем же уравнением регрессии. Пусть имеется две выборки с переменными y,x1,…,xk объемом n1 и n2 и в каждой зависимость yi от регрессоров описываются уравнениями: Пусть RSS1 = 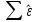 i2 RSS1 = i2 RSS1 = 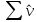 i2 - остаточные суммы квадратов в модели регрессии, оцененной по первой и второй выборкам соответственно. i2 - остаточные суммы квадратов в модели регрессии, оцененной по первой и второй выборкам соответственно.Обозначим через RSS=  i2 остаточную сумму кввадратов в модели регрессии, оцененной по объединенной выборке объема n1 + n2 i2 остаточную сумму кввадратов в модели регрессии, оцененной по объединенной выборке объема n1 + n2Статистический критерий проверки нулевой гипотезы об однородности выборок. H0:  12= 12= 22, 22,H1: 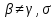 12= 12= 22. 22.F =  Следовательно, при заданном уровне значимости  нулевая гипотеза отвергается при F>Fтабл где Fтабл=F( нулевая гипотеза отвергается при F>Fтабл где Fтабл=F( |
