3, 4-практ. сабақ АжСТ. 3 практикалы саба Бірдей лшемді матрицаларды осу. Матрицаны сана кбейту. Матрицаларды кбейту. Матрицаларды транспонирлеу
 Скачать 138.58 Kb. Скачать 138.58 Kb.
|
|
№ 3 практикалық сабақ Бірдей өлшемді матрицаларды қосу. Матрицаны санға көбейту. Матрицаларды көбейту. Матрицаларды транспонирлеу.   A= A= AТ= AТ= 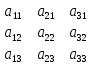 ; AТ-транспонирленген матрица ; AТ-транспонирленген матрица1-мысал. 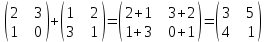 . .2-мысал. 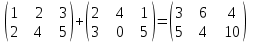 . .3-мысал. 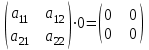 . .4-мысал. 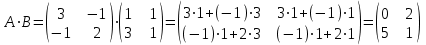 . .5-мысал. 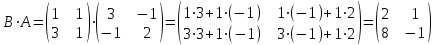 . .6-мысал. 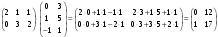 . .7-мысал. 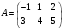 , , 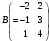 матрицалары берілген. матрицалары берілген. 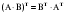 теңдікті дәлелдеңіз. теңдікті дәлелдеңіз.Шешуі.  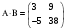 ; ; 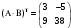 . . 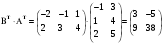 . .Сонымен, теңдік дәлелденді. 8-мысал. 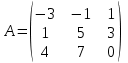 , , 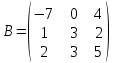 , , 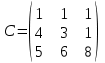 матрицалары берілген. матрицалары берілген. 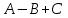 матрицасын табалық. матрицасын табалық.Шешуі. 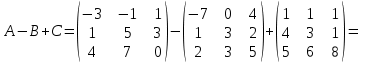 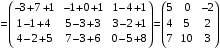 . .9-мысал. 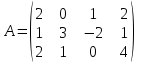 және және 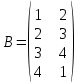 матрицалары берілген. матрицалары берілген. 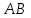 және және 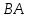 көбейтінділерін табалық. көбейтінділерін табалық. Шешуі. а) 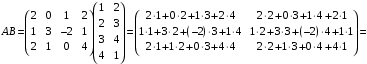 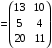 . .б) 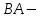 орындалмайды. орындалмайды.10-мысал. Мына матрицаларға көрсітілген амалдарды орындаңыз: Мұндағы  , ,  . . Шешуі.  , , . .Матрицаларды қосу A және B матрицаларын қосу үшін әуелі олардың өлшемдіктері тең болуы қажет. Онда 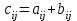 теңдігімен алынған матрицасы теңдігімен алынған матрицасы 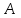 және және 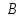 матрицасының қосындысы деп саналады, яғни онда матрицасының қосындысы деп саналады, яғни онда 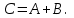 11-мысал. 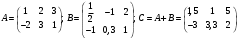 Матрицаны матрицаға көбейту 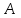 матрицасын матрицасын 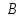 матрицасына көбейту үшін бірінші матрицаның бағана саны мен екінші көбейтіш матрицаның жолдар саны тең болуы керек. Басқа жағдайларда матрицаларды көбейту амалы анықталмайды. матрицасына көбейту үшін бірінші матрицаның бағана саны мен екінші көбейтіш матрицаның жолдар саны тең болуы керек. Басқа жағдайларда матрицаларды көбейту амалы анықталмайды. 12-мысал. 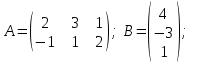 Табу керек A және B матрицаларының көбейтіндісін Табу керек A және B матрицаларының көбейтіндісінЕскерту!  1) 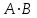 анықталғанымен анықталғанымен 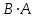 анықталмауы мүмкін. анықталмауы мүмкін.2) 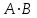 және және 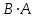 анықталғанымен, мүмкін анықталғанымен, мүмкін 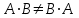 . .13-мысал. 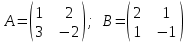 , , 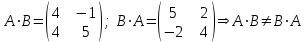 . .№ 4 практикалық сабақ Сызықтық тәуелділік. Векторлар жүйесінің базисі. 1-есеп 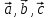 векторлары базис құратынын дәлелдеңіз және осы базистегі векторлары базис құратынын дәлелдеңіз және осы базистегі 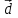 векторының координаталарын табыңыз, векторының координаталарын табыңыз, 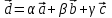 . . 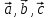 векторлары үшін келесі шарт орыналады векторлары үшін келесі шарт орыналады 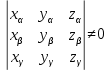 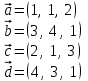 болсын болсын Шешуі: 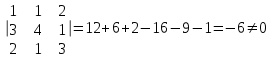 егер 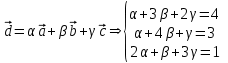 X, Y, Z векторларын X, Y, Z векторларын 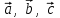 вектрларына, вектрларына, 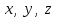  векторын векторын 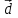 векторына теңестіреміз, сонымен векторына теңестіреміз, сонымен 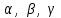 - ны табамыз: - ны табамыз:  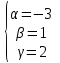 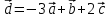 2-есеп. Шешуі. 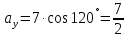 , ,  болады. Осыдан болады. Осыдан  . . 3-есеп. Шешуі. Алдымен  . Осы теңдеу жүйесін шешіп, оның . Осы теңдеу жүйесін шешіп, оның 4-есеп 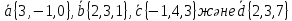 векторлары берілген. Табу керек: векторлары берілген. Табу керек: 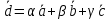 Уйге тапсырма: СӨЖ
|

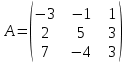 және
және 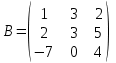 матрицасы берілген.
матрицасы берілген. 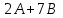 матрицасын табыңыздар.
матрицасын табыңыздар. 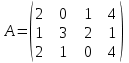 және
және 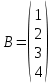 матрицалары берілген.
матрицалары берілген. 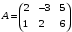 және
және 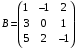 матрицалары берілген.
матрицалары берілген. 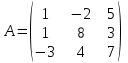 матрицасының
матрицасының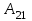 алгебралық толықтауышын табыңыздар.
алгебралық толықтауышын табыңыздар. көбейтіндісін табыңыздар.
көбейтіндісін табыңыздар.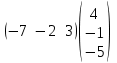 көбейтіндісін табыңыздар.
көбейтіндісін табыңыздар.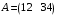 және
және 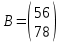 матрицалары берілген.
матрицалары берілген.