бдр18. 3 Расчетные сочетания усилий
 Скачать 0.56 Mb. Скачать 0.56 Mb.
|
|
3.1. Расчетные сочетания усилий Усилия в расчетных сечениях балок типа БДР
3.2. Выбор типа опалубочной формы Примем первый тип опалубочной формы стропильной балки как для первого снегового района строительства. 3.3. Расчет нижнего пояса 3.3.1. Подбор арматуры 1. Дано: - расчетные усилия в сечении: N = 2361.94 кН, M = 52.79 кН∙м; - размеры поперечного сечения b = 0,2 м; h = 0,3 м; - величина защитного слоя бетона ap = ap' = 0,06 м; - класс ПН арматуры А600. 2. Rs=520 МПа. 3. Рабочая высота сечения h0 = 0.3-0.06 = 0.24 м; 4. Эксцентриситет продольного усилия относительно центра тяжести сечения 5. Эксцентриситет продольного усилия относительно граней сечения соответственно верхней и нижней: 6. Коэффициент 7. Площадь растянутой и сжатой арматуры (3.3) 8. Принимаем нижнюю арматуру 3Ø36 А800 Asp = 3054 мм2, dsp = 22мм, а верхнюю 2Ø32 А800 A’sp = 1609 мм2, d’sp = 32 мм. 3.3.2 Образование трещин 1. Дано: - класс бетона В35; - условия твердения – подвергнутый тепловлажностной обработке; - способ натяжения арматуры – механический; - средний коэффициент надежности по нагрузке γfm=1,249; - длина растянутого пояса l=18,0 м 2. Нормативная прочность бетона при растяжении Rbt,ser = 1.95 МПа, модуль упругости бетона Eb =34500 МПа, нормативная прочность арматуры Rs,ser = 600 МПа, модуль упругости арматуры Es=200000 МПа. 3. Назначаем величину предварительных напряжений 4. Коэффициент неблагоприятного влияния ПН γsp= 0,9. 5. Величина предварительных напряжений: σsp = σsp = 0.9∙540 = 486 МПа (3.5). 6. Потери от релаксации арматуры: Δσsp1 = 0.1∙σsp – 20 = 0,1∙486 – 20=28,6 МПа (3.6). 7. Потери от перепада температуры при тепловлажностной обработки бетона: Δσsp2 = 1.25∙Δt = 1,25∙65 = 81,25 МПа. (3.7) 8. Потери от деформации стальной формы Δσsp3 =30 МПа (при механическом способе натяжения). 9. Потери от деформации анкеров: 10. Первые суммарные потери: 11. εb,sh=0,0002 для бетона класса B35. 12. Потери от усадки бетона Δσsp5 = εb,sh∙Es = 0,0002∙200000 = 40 МПа (3.10) 13. Коэффициент ползучести φb,сr=2.1 (по табл. 2.6 [4]). 14. Коэффициент приведения арматуры к бетону: α = Es/Eb = 200000/34500 = 5,8 (3.11) 15. Коэффициент армирования сечения: 16. Усилие предварительного обжатия с учетом первых потерь: P(1) = (Asp + A’sp)(σsp – σlos,1) = (3054+1609)∙(486 -160,903)∙10-3=1515,93 кН (3.13) 17. Приведенная площадь сечения: Ared = bh + αAsp + αA’sp = 0.2∙0.3 + 5.8∙3054∙10-6+ 5.8∙1609∙10-6=0.087 м 2(3.14) 18. Приведенный статический момент: 19. Центр тяжести приведенного сечения относительно наиболее растянутой грани: 20. Момент инерции бетонного сечения: 21. Момент инерции нижней и верхней арматуры: 22. Приведенный момент инерции сечения: 23. Расстояние от центра тяжести приведенного сечения до центра тяжести арматуры, соответственно нижней и верхней: (3.21) 24. Эксцентриситет усилия обжатия с учетом первых потерь: 25. Напряжения в бетоне на уровне центра тяжести нижней и верхней арматуры: 26. Потери от ползучести бетона:  (3.25) (3.25)  (3.26) (3.26) 27. Вторые суммарные потери в верхней и нижней арматуре: (3.27) 28. σbp > 0, т.е. потери от ползучести следует учитывать. 29. Проверяем условие: 30. Предварительное напряжение с учетом всех потерь: (3.29) 31. Коэффициент учета пластичности: γ = 1.3. 32. Упругий момент сопротивления приведенного сечения: 33. Ядровое расстояние: 34. Усилие обжатия с учетом всех потерь: 35. Эксцентриситет усилия обжатия с учетом всех потерь: 36. Момент трещиностойкости: 37. Нормативное усилие от постоянной и полной снеговой нагрузки: 38. Момент усилия Ntot относительно ядровой точки: 39. Проверка трещиностойкости: Трещины образуются, требуется расчет по их раскрытию. 3.3.3. Раскрытие трещин 1. Дано: - усилие от постоянной нагрузки Ng = 1472.46 кН; - предельно допустимая ширина непродолжительного раскрытия трещины acrc = 0.4 мм; - предельно допустимая ширина продолжительного раскрытия трещины a’crc = 0.3 мм; 2. Коэффициент учитывающий долю длительной составляющей снеговой нагрузки kl = 0.5. 3. Длительнодействующая продольная сила: 4. Значение продольной силы в момент образования трещины: 5. Расстояние от центра тяжести приведенного сечения до точки приложения продольной силы: 6. Расстояние от центра тяжести приведенного сечения до точки приложения усилия обжатия P: 7. Плечо внутренней пары сил: 8.1. Напряжения в растянутой арматуре от усилия Ntot: 8.2. Напряжения в растянутой арматуре от усилия Nl: 8.3. Напряжения в растянутой арматуре от усилия Ncrc: 9. Проверка условия: т.е. прочность нижней арматуры на разрыв обеспечена. 10. Поправочный коэффициент, учитывающий пластичность – k = 0.9 (п. 4.10[4]). 11. Высота растянутой зоны как для упругого материала:  (3.46) (3.46)12. Высота растянутой зоны с учетом пластичности: 13. Проверяем условие: Так как условие не выполняется, то: 14. Проверяем условие: 15. Площадь сечения растянутого бетона: 16. Базовое расстояние между трещинами: 17.1. Коэффициент совместной работы бетона и арматуры при полной нагрузке: 17.2. Коэффициент совместной работы бетона и арматуры при постоянной и временной длительной нагрузке: 18. Опытные коэффициенты: φ1= 1 φτ1=1.4 φ2= 0.5. 19.1. Ширина раскрытия трещин от длительного действия постоянных и временных длительных нагрузок: 19.2. Ширина раскрытия трещин от кратковременного действия полной нагрузки: 19.3. Ширина раскрытия трещин от кратковременного действия постоянных и временных длительных нагрузок: 20. Продолжительная ширина раскрытия трещин: Непродолжительная ширина раскрытия трещин: 21. Проверяем условие: 3.3.4. Наклонное сечение 1. Дано: - максимальная поперечная сила на опоре Qmax = 68.05 кН, - класс конструктивной арматуры B500. 2. Коэффициент учета влияния длительной нагрузки на прочность бетона γb1 = 0.9. 3. Табличные значения прочности бетона при сжатии Rb = 19.5 МПа, при растяжении Rbt = 1.3 МПа, прочность конструктивной арматуры на срез – Rsw = 300 МПа. 4. Прочность бетона с учетом длительности нагрузки: 5. 6. 7. Коэффициент учета предварительного обжатия в наклонном сечении:  (3.64) (3.64)8. Момент в наклонном сечении, воспринимаемый бетоном: 9. Длина проекции наклонного сечения: 10. Поперечная сила воспринимаемая бетоном: 11. Поперечная сила в конце наклонного сечения: 12. Проверка условий: 13. Поперечная арматура требуется. 14. Шаг поперечных стержней: 15. Диаметр поперечных стержней: dsw = 4 мм. 16. 17. Определяем интенсивность хомутов: Определим площадь хомутов: 2Ø6 мм B500 Asw = 57 мм2. 18. Проверим выполнение условия: 19. Проверим выполнение условия: 20. 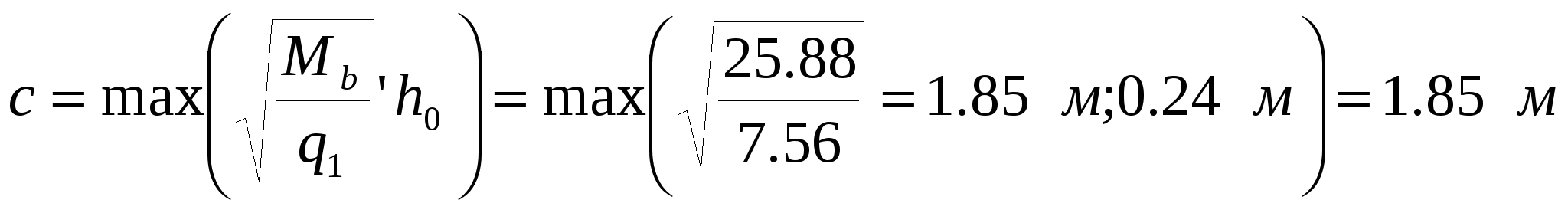 (3.77) (3.77)21. 22. а) Проверка условия: б) 22’. 23. Проверка условия: 24. 25. Поперечная сила, воспринимаемая хомутами в наклонном сечении: 26. Проверка условия прочности: 27. 28. sw = 150 мм, dsw = 6 мм. 3.4. Расчет верхнего пояса 3.4.1. Подбор арматуры 1. Дано: - расчетные усилия в сечении: N = 2377.2 кН, M = 116.87 кН∙м; - размеры поперечного сечения b = 0.2 м, h = 0.42 м; - величина защитного слоя бетона a = a’ = 0.04 м; - класс простой арматуры A300; - длина панели верхнего пояса l = 1.5 м. 2. Rs = Rsc = 270 МПа. 3. Величина случайного эксцентриситета: 4. Расчетная длина панели верхнего пояса: 5. 6. Рабочая высота сечения: 7. Эксцентриситет продольного усилия относительно центра тяжести сечения: 8. Эксцентриситет продольного усилия относительно растянутой грани сечения: 9. Граничная высота сжатой зоны: 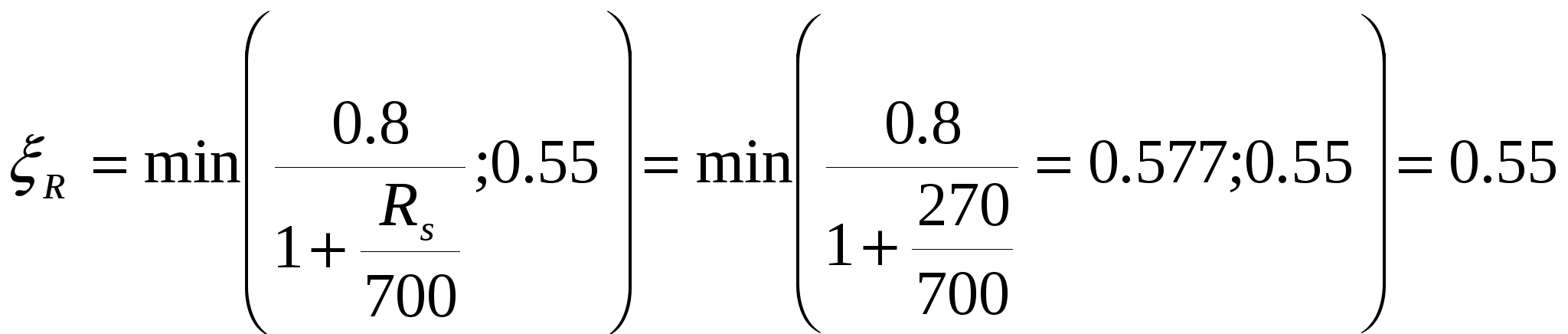 (3.90) (3.90)10. Предельный коэффициент граничной высоты сжатой зоны: 11. Площадь сжатой арматуры: 12. Площадь растянутой арматуры: 13. Принимаем верхнюю арматуру 3Ø40A300 As = 3770 мм2, ds = 40 мм, а нижнюю 2Ø12A300 A’s = 226 мм2, d’s = 12 мм. 3.4.2. Наклонное сечение 1. Дано: - поперечная сила Q = 100.55 кН. 2. Модуль упругости простой арматуры A300 Es = 200000 МПа. 3. Максимальная поперечная сила в наклонном сечении: 4. Момент в наклонном сечении, воспринимаемый бетоном: 5. Длина проекции наклонного сечения: 6. Поперечная сила воспринимаемая бетоном: 7. Коэффициент приведения арматуры к бетону: 8. Приведенная площадь сечения: 9. Приведенный статический момент: 10. Центр тяжести приведенного сечения относительно наиболее растянутой грани: 11. Момент инерции бетонного сечения: 12. Момент инерции верхней и нижней арматуры: 13. Приведенный момент инерции сечения: 14. Поперечная сила воспринимаемая бетоном до образования трещин: 15. Уточненная поперечная сила воспринимаемая бетоном: 16. Поперечная сила в конце наклонного сечения: 17. Проверка условий: Поперечная арматура требуется. 18. Шаг поперечных стержней: 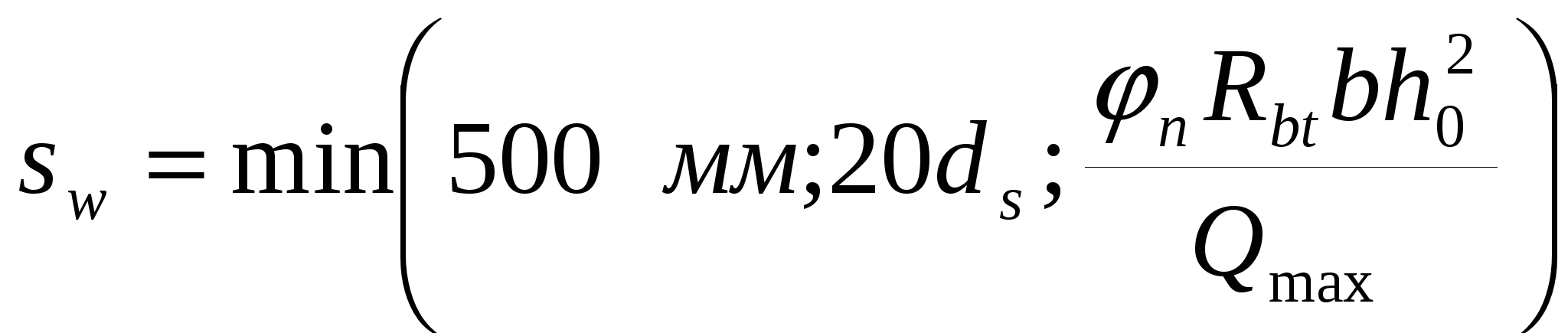 (3.111) (3.111)19. Диаметр поперечных стержней: dsw = 4 мм. 16. 17. Определяем интенсивность хомутов: Определим площадь хомутов: 2Ø8 мм B500 Asw = 101 мм2. 18. Проверим выполнение условия: 19. Проверим выполнение условия: 20. 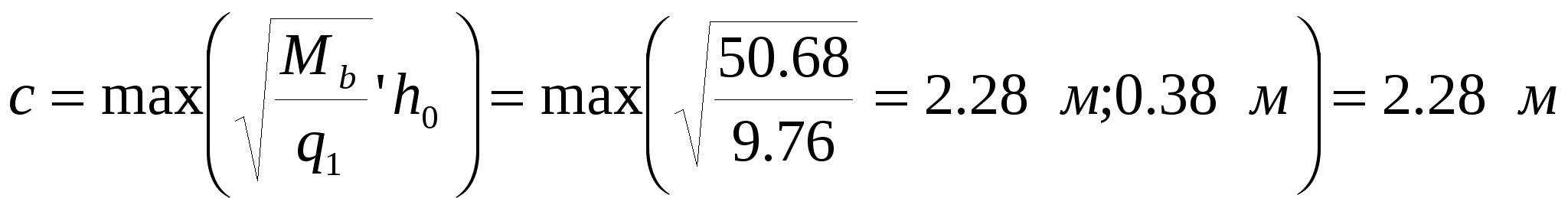 (3.117) (3.117)21. 22. а) Проверка условия: б) 22’. 23. Проверка условия: 24. 25. Поперечная сила, воспринимаемая хомутами в наклонном сечении: 26. Проверка условия прочности: 27. 28. sw = 500 мм, dsw = 8 мм. 3.5. Расчет стоек 1. Дано: - расчетные усилия в сечении: N = 5.26 кН, M = 44.78 кН∙м; - размеры поперечного сечения: b = 0.2 м, h = 0.5 м; -величина защитного слоя бетона: ap = a’p = 0.04 м; - класс простой арматуры: A400; - длина панели верхнего пояса l = 1.5 м. 2. Величина случайного эксцентриситета: 3. Расчетная длина панели верхнего пояса: 4. 5. Рабочая высота сечения: 6. Эксцентриситет продольного усилия относительно центра тяжести сечения: 7. Эксцентриситет продольного усилия относительно растянутой грани сечения: 8. Граничная высота сжатой зоны: 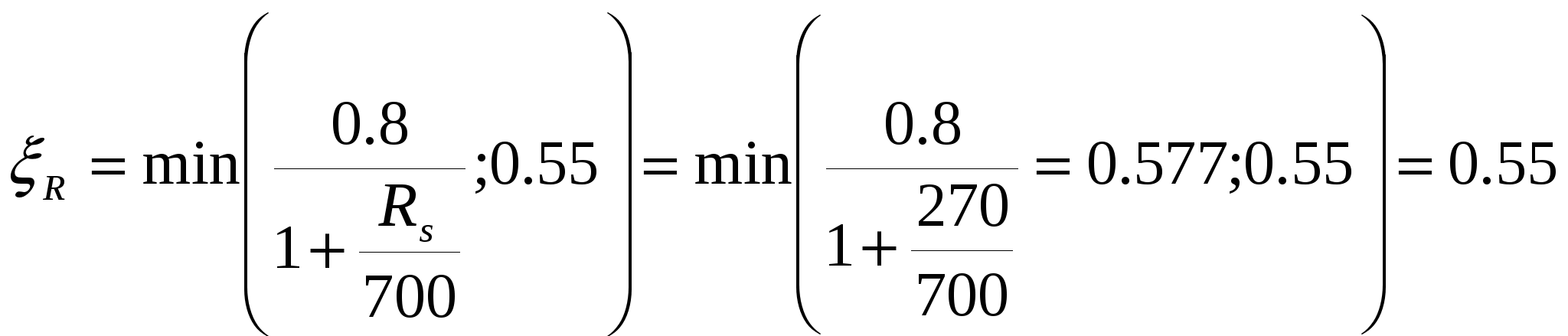 (3.129) (3.129)9. Предельный коэффициент граничной высоты сжатой зоны: 10. Площадь сжатой арматуры: 11. Определяем коэффициент относительной высоты сжатой зоны бетона: 12. Площадь растянутой арматуры: 13. Принимаем нижнюю арматуру 2Ø10A300 As = 157 мм2, ds = 10 мм, а верхнюю 2Ø16A300 A’s = 402 мм2, d’s = 16 мм. 3.6. Расчет опорного узла 1. Дано: - поперечная сила Qmax = 675.17 кН; - ширина и высота сечения опорной части b = 0.2 м, h1 = 0.89 м; - величина защитного слоя бетона a = a’ = 0.06 м. 2. Длина проекции наклонного сечения с = 2.85 м. 3. Рабочая высота сечения: 4. Момент воспринимаемый бетоном: 5. Поперечная сила воспринимаемая бетоном: 6. Проверка условия: 7. Проверка условия: 8. Проекция наклонного сечения при нагрузке в виде сосредоточенной силы: 9. Поперечная сила в таком сечении 10. Параметр 11. Параметр 12. Параметр 13. Предельное значение параметра 14. Проверяем условие: 15. Требуемая интенсивность хомутов: 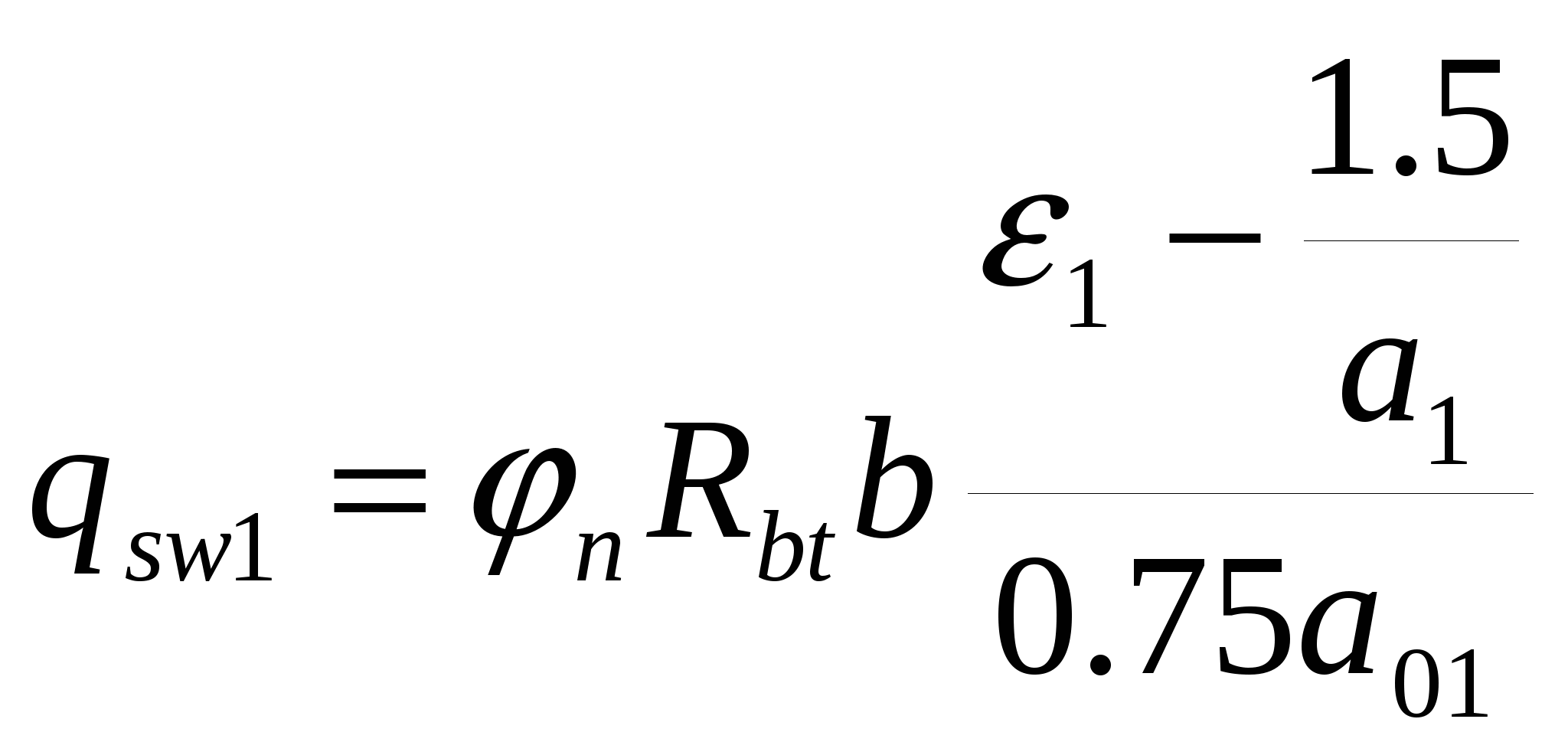 (3.146) (3.146)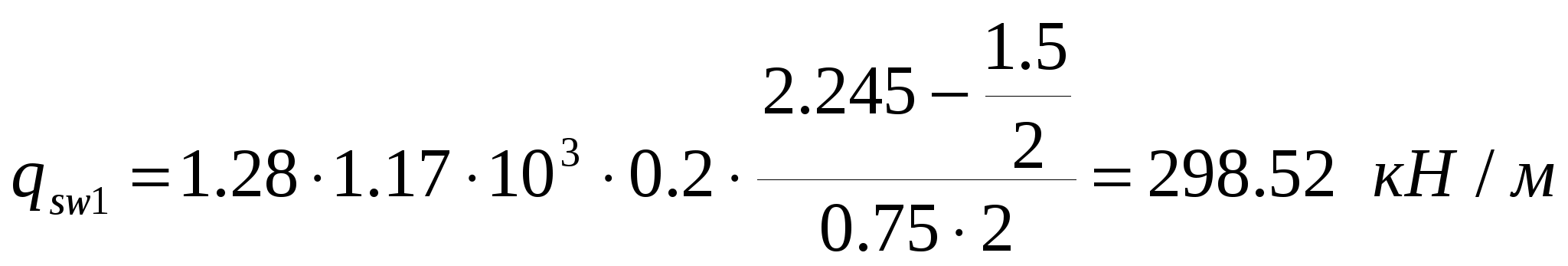 (3.147) (3.147)16. 17. Конструктивный шаг поперечных стержней: 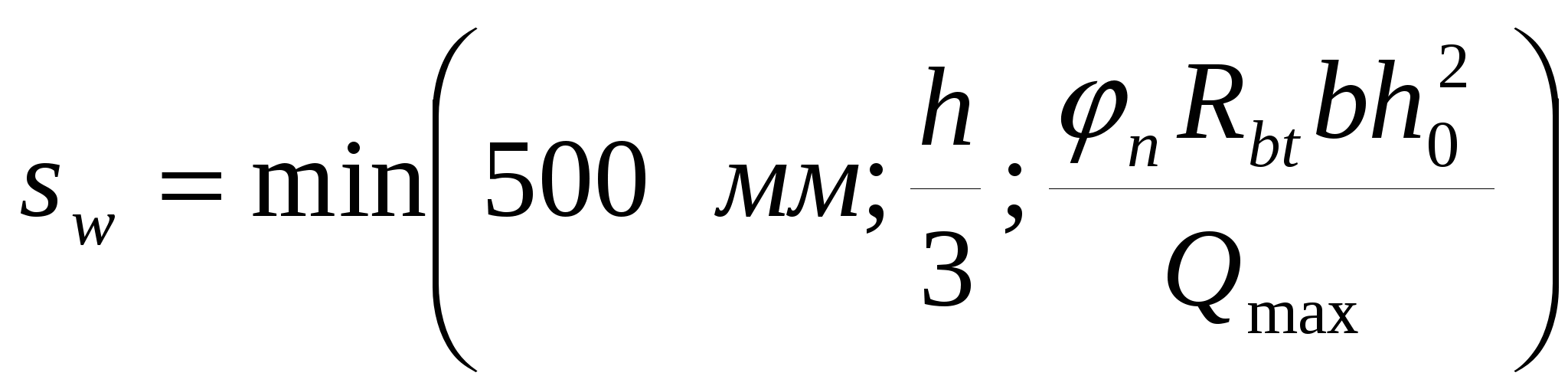 (3.148) (3.148)Примем s = 200 мм. 18. Требуемая площадь поперечной арматуры при 2 стержнях в сечении: 19. Принимаем поперечную арматуру 2Ø14 А-300 Asw = 308 мм2 с шагом s = 200 мм. Так как в верхнем и нижнем поясах балки требуется арматура большого диаметра, то для обеспечения совместной работы бетона с арматурой, принимаем 3-ю опалубочную форму БДР шириной 280 мм. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
