редуктор. 03 Вопрос Выбор материалов зубчатой передачи. 3 Выбор материалов зубчатой передачи. Определение допускаемых напряжений
 Скачать 44.86 Kb. Скачать 44.86 Kb.
|
|
3 Выбор материалов зубчатой передачи. Определение допускаемых напряжений 3.1. Выбор твердости, термообработки и материала колеса а) К зубчатому колесу применим твердость ≤ 350 НВ, при этом обеспечивается чистое нарезание зубьев после термообработки, высокая точность изготовления и хорошая прирабатываемость зубьев. Для равномерного изнашивания зубьев и лучшей их прирабатываемости твердость шестерни НВ1 назначим больше твердости колеса НВ2 и измерим по шкале Роквела ≥45 HRCЭ НВ1 - НВ2 ≥70 б) Определим марку стали : - для шестерни – 40Х, твердость ≥ 45 HRCЭ ; - для колеса – 40Х, твердость ≤350 НВ2, в) По таблице определим механические характеристики стали 40Х: - для шестерни – твердость 45…50 HRCЭ1, термообработка – улучшение и закалка ТВЧ, Dпред = 125 мм, Dпред – предельно допустимый диаметр заготовки шестерни. - для колеса – твердость 269…302 НВ2, термообработка – улучшение, Sпред = 80 мм, Sпред – предельно допустимая толщина заготовки обода и диска колеса. г) Определим среднюю твердость зубьев шестерни и колеса: HRCЭ1ср = ( 45 + 50 ) / 2 = 47,5; НВ2ср = ( 269 +302 )/2= 285,5 По графику находим НВ1ср = 457 3.2 Определяем допускаемые контактные напряжения 1. Рассчитываем коэффициент долговечности KHL . Наработка на весь срок службы: - для колеса N2 = 573 ω2 Lh = 573·5,37·26,28·103= 80,86·106 циклов где N – число циклов нагружения зубьев колеса за весь срок службы – наработка, где ω2 - угловая скорость колеса, ω2 = 5,37 рад/с; Lh – срок службы привода, Lh = 26,28·103 лет -для шестерни N1 = N2 uзп = 404,3·106 циклов где uзп – передаточное число передачи В зависимости от средних твердостей поверхностей HRCЭ1ср и НВ2ср находим NHO1 = 69.9 · 106 циклов NHO2 = 22,5 · 106 циклов Так как ‚N1 > NHO1 и N2 > NHO2, то коэффициенты долговечности KHL1 =1 и KHL2 = 1. б) По таблицам определяем допускаемое контактное напряжение [σ]НО соответствующее числу циклов перемены напряжений NHO: - для шестерни [σ]НО1 =14НRCЭ1ср +170=14·47,5+170=835 Н/мм2 - для колеса [σ]НО2 = 1,8 НВ 2ср+67= 664,9 Н/мм2 в) Определяем допускаемое контактное напряжение: - для шестерни [σ]Н1 = KHL1· [σ]НО1 = 835 Н/мм2 - для колеса [σ]Н2 = KHL2∙ [σ]НО2 = 580,9 Н/мм2 Так как НВ1 - НВ2 = 457 – 285,5 ≥70 и НВ 2ср = 285,5 < 350 НВ, то передача рассчитывается на прочность по среднему допускаемому контактному напряжению [σ]Н =0,45 ([σ]Н1 + [σ]Н2 )= 0,45(835 + 664,9)= 675 Н/мм2 При этом условие [σ]Н =675 Н/мм2 [σ]Н2 = 1,23∙ 664,9 = 817,8 Н/мм2 соблюдается. 3.3 Определяем допускаемые напряжения изгиба для зубьев шестерни [σ]F1 и колеса [σ]F2 . а) Рассчитываем коэффициент долговечности KFL Наработка за весь срок службы: для шестерки N1 = 501,95·106 циклов, для колеса N2 = 100,39·106 циклов. Число циклов перемены напряжений, соответствующее пределу выносливости, NFO = 4·106 для обоих колес. Так как N1 > NFO1, и N2 > NFO2, то коэффициенты долговечности КFL1 = 1 и КFL2 = 1 б) Определяем допускаемое напряжение изгиба, соответствующее числу циклов перемены напряжений NFO, - для шестерни [σ]FО1 = 310 Н/мм2 - для колеса [σ]FО2 =1,03· НВ 2ср =1,03 · 362 = 373 Н/мм2 в) Определяем допускаемое напряжение изгиба: - для шестерни [σ]F1 = КFL1[σ]FО1 = 1·310 = 310 Н/мм2 - для колеса [σ]F2 = КFL2[σ]FО2 = 1·373 = 373 Н/мм2 4. Расчет закрытой цилиндрической косозубой зубчатой передачи 4.1. Проектный расчет 1. Определим межосевое расстояние аw, мм: аw ≥ Ка (u +1) 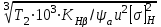 = = = 43 (5+1) 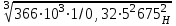 = = 119,917 мм 119,917 мм где: а) Ка—вспомогательньий коэффициент; для косозубых Ка = 43 б) ψ а = b2 / аw – коэффициент ширины венца колеса, равный 0,28...О,36 в) u- передаточное число редуктора, u = 5 г) Т2 — вращающий момент на тихоходом валу редуктора, Т2 = 366 Нм д) [ σ ]Н - допускаемое контактное напряжение колеса, [ σ ]Н = 675 Н/мм2 е) КНβ— коэффициент неравномерности нагрузки по длине зуба, для прирабатывающихся зубьев КНβ = 1 Полученное значение межосевого расстояния округлим до ближайшего значения из ряда нормальных линейных размеров аw = 120 мм 2. Определим модуль зацеплеяия m, мм: m ≥ 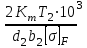 = =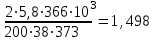 где а) Кm - вспомогательный коэффициент; для косозубых Кm = 5,8 б) d2 - делительный диаметр колеса, d2 = 2 аwu/(u+1)=2·120·5/(5+1) = 200 мм в)b2— ширина веyца колес b2 = ψ а аw = 0,32·120 = 38 мм, ψ а – коэффициент ширины венца колеса, равный 0,28...О,36 Полученное значение модуля m округлим в большую сторону до стандартного из ряда чисел. m =1,5 Определим угол наклона зубьев βmin для косозубых передач βmin = arcsin 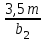 = arcsin = arcsin = 80 = 80В косозубых передачах угол наклона зубьев принимают βmin = 8…16о 3. Определим суммарное число зубьев шестерни и колеса для косозубых колес z∑ = z1 + z2 = 2 аwcos βmin / m =2·120· cos 80/1,5=158,448 Полученное значение z∑ округлим в меньшую сторону до целого числа. z∑ = 158 4. Определим число зубьев шестерни: z1 = z∑ / 1 +u=158/1+5=26,33 Значение z1 округлим до ближайшего целого числа , при этом для уменьшения шума и отсутствия подрезания зубьев z1 ≥ 18 z1 = 26 5. Определим число зубьев колеса : z2 = z∑ - z1 =158-26=132 6. Определим фактическое передаточное число передачи и проверим его отклонение от заданного: uф = z2 / z1 = 132/26=5,08 ∆u = 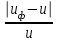 100% = 100% =  100% =1,6% ≤ 4 % 100% =1,6% ≤ 4 %7. Определим фактическое межосевое расстояние: для косозубых передач аw = (z1 + z1)m/2cos β= (26 + 132)·1,5/2 cos 80β ·=119,67 мм≈120 мм 8. Определим основные геометрические параметры передачи, а) шестерня: - Диаметр делительной окружности: для косозубых передач d1= m z1/ cos β =1,5·26/ cos β=40 мм - Диаметр вершин зубьев: da1 = d1+2 m = 40+2·1,5=43 мм - Диаметр впадин зубьев: df1 = d1- 2,4 m =40-2,4·1,5=36 мм - Ширина зубчатого венца: b1 = b2 + (2…4) = 38+4=42 мм в) колесо: - Диаметр делительной окружности: для косозубых передач d2= m z2 / cos β=1,5·132/ cos 80=200 мм - Диаметр вершин зубьев: da2 = d2+2 m = 200+2·1,5=203 мм - Диаметр впадин зубьев: df2 = d2- 2,4 m = 200-2,4·1,5=196 мм - Ширина зубчатого венца: b2 = ψ а аw = 0,32·120=38 мм ψ а – коэффициент ширины венца колеса, равный 0,28...О,36 4.2 Проверочный расчёт 1. Проверим межосевое расстояние: аw = (d1+d2)/ 2 = (40+200)/2=120 мм 2. Проверим пригодность заготовок колес: - шестерни: Dзаг = da1 + 6 = 43+6=49 мм Условие Dзаг ≤ Dпред выполняется. где Dпред = 125 мм, Dпред – предельно допустимый диаметр заготовки шестерни - колеса: Sзаг = b2 + 4 = 38+4 = 42 мм Условие Sзаг ≤ Sпред выполняется. где: Sпред = 80 мм, Sпред – предельно допустимая толщина заготовки обода и диска колеса. 3. Проверим контактные напряжения σ Н, Н/мм2 σ Н = K  где [ σ ]Н = 675 Н/мм2, uф – фактическое передаточиое число передачи, uф = 5 d2 – диаметр делительной окружности, d2 = 200 мм b2 - ширина зубчатого венца, b2 = 38 мм К - вспомогательный коэффициент, К = 436 Ft – окружная сила в зацеплении Ft = 2Т2· 103 / d2 = 2·366· 103 / 200 =3660 Н Т2 – вращающий момент (из таблицы 2.4) Т2 = 366 Нм KHα – коэффициент, учитывающий распределение нагрузки между зубьями, KHα = 1,1. KHβ – коэффициент неравномерности нагрузки по длине зуба, для прирабатывающихся зубьев, КНβ = 1 KHν – коэффициент динамической нагрузки, зависящий от окружной скорости колес и степени точности передачи, KHν=1,1 Допускается: - недогрузка σ Н < [ σ ]Н не более 10% - перегрузка σ Н > [ σ ]Н до 5 % σ Н = 376· 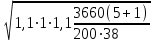 = 703 Н/мм2 = 703 Н/мм2 Непегруз - 4% Условие выполняется 4. Проверить напряжения изгиба зубьев шестерни σ F1 и колеса σ F2 .Н/мм2 - для колеса: σ F2 = YF2 Yβ 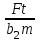 KFα KFβ KFν ≤ [σ] F2 KFα KFβ KFν ≤ [σ] F2- для шестерни: σ F1 = σ F2 YF1/ YF2 ≤ [σ] F1 где: m—модуль зацепления, m = 1,5 мм; b2 – ширина зубчатого венца колеса, b2 = 38 мм; Ft – окружная сила в зацеплении Ft = 2Т2· 103 / d2 = 2·366· 103 / 200 =3660 Н Т2 – вращающий момент, Т2 = 366 Нм d2 – диаметр делительной окружности, d2 = 200 мм KFα - коэффициент, учитывающий распределение нагрузки между зубьями. KFα = 1. KFβ - коэффициент неравномерности нагрузки по длине зуба. для прирабатывающихся зубьев колеса KFβ = 1 . KFν - коэффициент динамической нагрузки, зависящий от окружной скорости колес и степени точности передачи, примем степень точности 9, KFν = 1. YF1 и YF2 - коэффициенты формы зуба шестерни и колеса. Определим в зависимости от числа зубьев шестерни и колеса, YF1 = 4,07, YF2 = 3,62. Для косозубых передач в зависимости от эквивалентного числа зубьев - шестерни zv1 =z1/ cos3β =26/0,955= 27,23 - колеса zv2 =z2/ cos3β = 132/0,955 = 138,22 угол наклона зубьев - β Yβ - коэффициент, учитывающий наклон зуба, Yβ = 1. [σ] F1 и [σ] F2—допускаемые напряжения изгиба шестерни и колеса, Н/мм2 Напряжения изгиба зубьев колеса - для колеса: σ F2 = 3,62 1 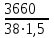 1 1 1=232,442≤ [σ] F2 1 1 1=232,442≤ [σ] F2- для шестерни: σ F1 = 232,442 4,07/ 3,62=261,337 ≤ [σ] F1 σ F2≤ [σ] F2 232,442 ≤ 373 σ F1 ≤ [σ] F1 261,337 ≤ 310 При проверочном расчете σ F значительно меньше [σ] F - это допустимо, так как нагрузочная способность большинства зубчатых передач ограничивается контактной прочностью. |
