динамика вращательного движения. 4. динамика вращательного движения твёрдого

• Название: 4. динамика вращательного движения твёрдого
• Дата: 11.04.2022
• Размер: 396 Kb.
• Имя файла: динамика вращательного движения.doc
• Тип: Документы; #463981

4. ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ТВЁРДОГО ТЕЛА

Для описания динамики вращательного движения потребуются дополнительные динамические характеристики. Поэтому начнём с определений этих динамических характеристик.
4.1. МОМЕНТ СИЛЫ
Из повседневного опыта известно, что в ряде случаев, прикладывая одну и ту же силу к разным точкам тела, можно получить разные результаты (например, попытайтесь открыть дверь, прикладывая одинаковую силу к ручке двери и где-нибудь вблизи дверных петель).

Количественной мерой воздействия, зависящего от точки приложения силы, является момент силы.

М 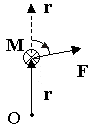омент силы относительно точки О - это векторная величина, равная векторному произведению радиуса-вектора r, соединяющего точку О и точку приложения силы, и силы F:

M=[r,F].

Модуль вектора момента силы M=rFsin, где -угол между векторами r и F.

Направление вектора Мопределяется по правилу правого винта: во-первых необходимо совместить начала перемножаемых векторов, затем поставить правый винт перпендикулярно плоскости, в которой лежат векторы-сомножители, и вращать его от вектора, записанного первым, к вектору, записанному вторым, в сторону наименьшего угла; направление поступательного движения винта покажет направление результирующего вектора (в приведённом на рисунке примере результирующий вектор направлен за рисунок). Размерность момента силы [М]=Н^.м, т.е. ньютон на метр.

Если на тело действуют несколько сил одновременно, то результирующий момент силы относительно некоторой точки О равен векторной сумме моментов всех сил относительно той же точки О:

M=M₁+M₂+…+M_N.

Е 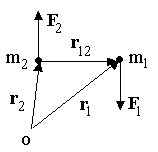сли к телу приложены две силы F₁и F₂, равные по величине и противоположные по направлению, то их суммарное действие характеризуют моментом пары сил. Момент пары сил равен сумме моментов сил F₁и F₂относительно одной точки О:

M=[r₁,F₁]+[r₂,F₂]=[r₁,F₁]-[r₂,F₁]=[(r₁-r₂₎,F₁]=[r₁₂,F₁];

Здесь учтено, что F₂=-F₁; вектор r₁₂ – вектор, соединяющий точки приложения сил F₁и F₂.

Если силы F₁и F₂не только равны по модулю, но и направлены вдоль прямой, соединяющей точки приложения сил, то угол между силой F₁ и радиус-вектором r₁₂ равен нулю. Поэтому момент такой пары сил равен нулю.

Проекция вектора момента силы на ось z, проходящую через точку О, называется моментом силы относительно оси

M 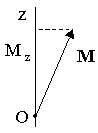_z=[r,F]_z.

Момент силы относительно оси является скалярной величиной.

Если на тело действуют несколько сил одновременно, то результирую­щий момент силы относительно оси z, проходящей через точку О, равен проекции результирующего момента всех сил относительно точки О на эту ось.

При решении задач удобно использовать другой вариант определения момента силы относительно оси:

M_z=F_R,

г 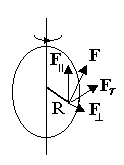де F_ - проекция вектора силы на касательную к траектории вращения, R - плечо силы (это кратчайшее расстояние между осью вращения и линией действия силы, равное rsina).

На рисунке показано вращающееся тело, к которому приложена сила F. Параллельная и перпендикулярная оси составляющие силы влияния на вращение тела не оказывают, так как ось закреплена. Третья составляющая силы F_τ, направленная по касательной к оси, и создаёт момент силы относительно оси M_z.
4.2. МОМЕНТ ИМПУЛЬСА
П 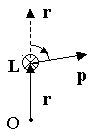усть дана материальная точка, имеющая импульс р. Пусть её положение относительно точки О определяется радиусом-вектором r. Движение такой точки характеризуют моментом импульса L.

Моментом импульса материальной точки относительно точки О называется векторная величина, равная векторному произведению радиуса-вектора rи вектора импульса p:

L=[r,p].

Модуль момента импульса L=rpsin, где  - угол между векторами rир. Направление вектора момента импульса определяется по правилу правого винта.

Размерность момента импульса [L]=кг^.м²/с.

М 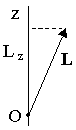омент импульса тела относительно точки равен векторной сумме моментов импульсов частиц тела относительно той же точки

L=L₁+L₂+…+L_N.

Проекция вектора момента импульса относительно точки О на ось z, проходящую через эту точку, называется моментом импульса относительно оси:

L_z=[r,p]_z.

Момент импульса относительно оси является скалярной величиной.

Момент импульса тела относительно оси zравен проекции момента им­пульса тела относительно точки О на ось z, проходящую через эту точку.
4.3. СВЯЗЬ МОМЕНТА СИЛЫ И МОМЕНТА ИМПУЛЬСА
Момент импульса и момент силы связаны между собой. Найдём выражение, связывающее их.

Возьмём производную по времени от выражения, определяющего момент импульса:



Член равен нулю, так как угол между вектором скорости dr/dt и вектором импульса р равен нулю.

Производная импульса по времени, имеющаяся во втором члене полу­ченного выражения, равна силе (второй закон Ньютона). Поэтому можем запи­сать полученное выражение в следующей форме:

.

Но [r,F]есть по определению момент силы Fотносительно той же точки О. Поэтому



т.е. скорость изменения момента импульса частицы равна моменту силы, действующему на эту частицу.

Проекция последнего уравнения на ось z выражает связь момента им­пульса относительно оси z и момента силы относительно той же оси.

.
4.4. ОСНОВНОЙ ЗАКОН ДИНАМИКИ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
Пусть твёрдое тело вращается относительно неподвижной оси z.

Выразим момент импульса твёрдого тела относительно оси вращения. Для этого представим твёрдое тело как совокупность элементарных масс. Момент импульса одной элементарной массы относительно оси z



Момент импульса всего тела равен сумме моментов импульсов всех эле­ментарных масс



Скорость v у разных элементарных масс различна, а угловая скорость одинакова.

Поскольку v=r,



Поскольку угловая скорость со одинакова для всех элементарных масс, её можно вынести за знак суммы



Введём обозначение . С учётом этого

L_z=J_z^..

Ранее мы получили, что момент импульса и момент силы связаны сле­дующим образом:

.

Заменив L_zна J_zω и с учётом того, что J_zс течением времени не изменяется, получаем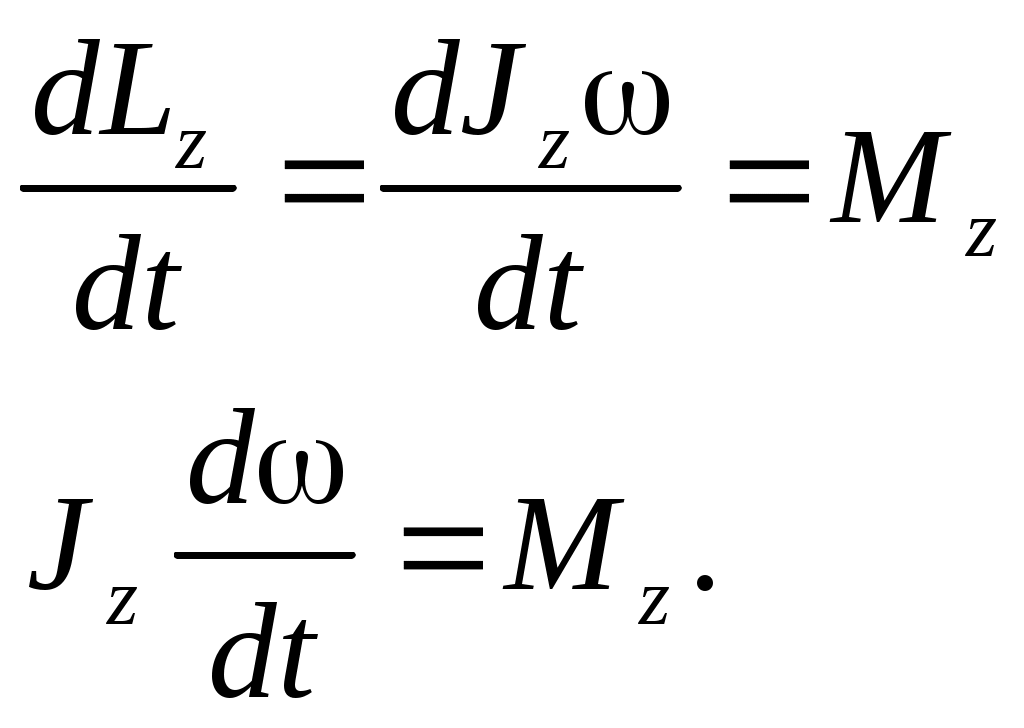



Учитывая, что производная угловой скорости по времени равна угловому ускорению , получаем

.

Полученное выражение - основной закон динамики вращательного движения, связывающий между собой меру внешнего воздействия - момент силы M_z с результатом внешнего воздействия - угловым ускорением .

Коэффициент J_z, стоящий в этом уравнении, зависит от массы тела и от то­го, как она распределена по объёму тела (это видно из определения величины J_z).

Чем меньше J_z, тем большее угловое ускорение получит тело при воздей­ствии момента силы M_z. Это говорит о том, что коэффициент J_z. характеризует инертность вращающегося тела. Поэтому J_zназывают моментом инерции тела относительно оси z.

Знание величины момента инерции тела необходимо для описания враща­тельного движения. Поэтому обсудим более подробно, что такое момент инер­ции и как его вычислить.
4.5. МОМЕНТ ИНЕРЦИИ ТЕЛА ОТНОСИТЕЛЬНО ОСИ ВРАЩЕНИЯ
Во вращательном движении в качестве меры инертности используется мо­мент инерции (тело одной и той же массы при вращении относительно разных осей обладает разной инертностью, поэтому массой в качестве меры инертно­сти вращающихся тел пользоваться нельзя).

Определение момента инерции



можно прочесть так: момент инерции тела относительно оси z равен сумме произведений элементарных масс на квадрат расстояния от оси вращения до данной элементарной массы.

Момент инерции есть величина скалярная.

Размерность момента инерции, как это видно из определения, [J]=кг^.м².

Из определения следует, что момент инерции - величина аддитивная, т.е. момент инерции системы из нескольких частиц равен сумме моментов инерции каждой из частиц.

Вычисление момента инерции производится путём интегрирования:



где dm - элементарная масса; dV- элементарный объём (объём, занимаемый элементарной массой); r - расстояние от элементарной массы до оси вращения;  - плотность тела в данной точке.

Вычисление этого интеграла в общем случае может быть довольно слож­ным, но если тело однородно, т.е. плотность тела во всех его точках одинакова, то плотность можно вынести за знак интеграла

.

В качестве примера рассмотрим расчёт момента инерции однородного диска относительно оси, перпендикулярной плоскости диска и проходящей через его центр.

Выделим в диске кольцо радиуса r шириной dr.

Масса этого кольца dm=dV=b2rdr, где b - толщина диска. Тогда момент инерции диска



(здесь учтено, что bR²=m - масса диска).

В 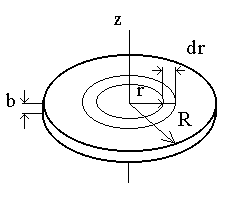ажно отметить, что момент инерции тела относительно разных осей различен (например, чем больше расстояние от материальной точки до оси вращения, тем больше её момент инерции).

Если этот же диск будет вращаться относительно оси, проходящей не через центр, то вы­числения станут намного сложнее. Но в ряде слу­чаев от необходимости интегрирования избавляет теорема Штейнера: момент инерции тела относительно произвольной оси вращения равен мо­менту инерции тела относительно оси, про­ходящей через центр масс тела параллельно оси вращения плюс произведение массы тела на квадрат расстояния между осями

J=J_o+ma².

Н 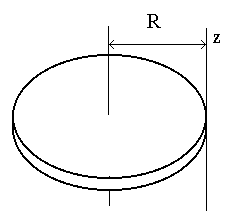апример, момент инерции диска отно­сительно оси z, перпендикулярной плоскости диска и проходящей на расстоянии Rот цен­тра масс тела, равен, по теореме Штейнера,

J=mR²/2 + mR²=3mR²/2.

4.6. ЗАКОН СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА
Рассмотрим систему частиц, на которые действуют как внутренние, так и внешние силы.

Момент импульса i-й частицы равен L_i=[r_i,p_i].

Момент импульса системы частиц, равный сумме моментов импульсов всех частиц, принадлежащих системе, можно выразить как



Производная момента импульса системы частиц по времени равна сумме производных моментов импульсов всех частиц, принадлежащих системе, а ка­ждая из этих производных, как было показано ранее, равна сумме моментов всех сил, действующих на i-ю частицу. Поэтому производную момента импуль­са системы по времени можно записать следующим образом:

.

Суммарный момент внутренних сил равен нулю, поскольку, в соответст­вии с третьим законом Ньютона, внутренние силы попарно равны по модулю, противоположны по направлению и направлены вдоль одной прямой. Как было отмечено в разд. 4.1, момент такой пары сил равен нулю. Следовательно,

,

т.е. момент импульса системы частиц изменяется под действием момента внешних сил.

Если суммарный момент внешних сил равен нулю, то

.

Нулю равна производная от константы, следовательно при момент импульса системы частиц постоянен во времени, т.е. L=const.

Таким образом, момент импульса системы материальных частиц будет постоянным во времени, если суммарный момент внешних сил равен ну­лю. Это и есть закон сохранения момента импульса.

Обратите внимание: момент импульса системы будет сохраняться и в том случае, когда сумма внешних сил отлична от нуля, но суммарный момент внешних сил равен нулю.
4.7. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ ВРАЩАЮЩЕГОСЯ ТЕЛА
Представим тело, вращающееся относительно оси z, как совокупность элементарных масс.

Скорость i-й элементарной массы, находящейся на расстоянии r, от оси вращения, v_i=r_i.

Её кинетическая энергия

.

Кинетическая энергия тела равна сумме кинетических энергий элементар­ных масс

.
4.8. РАБОТА ВНЕШНИХ СИЛ ПРИ ВРАЩЕНИИ ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ОСИ
Поскольку взаимное расположение частиц твёрдого тела при вращении не изменяется, элементарная работа внешних сил над телом будет равна прираще­нию кинетической энергии этого тела:

A=dW

или

.

Но d=dt, следовательно,

.

Таким образом, элементарная работа, совершаемая при вращении тела от­носительно неподвижной оси, равна произведению момента силы относительно оси вращения на элементарное угловое перемещение.

Работа на конечном угловом перемещении равна интегралу от элементар­ной работы, т.е.



Если момент силы с течением времени не изменяется, то работа рассчиты­вается гораздо проще

A=M^..
4.9. АНАЛОГИЯ МЕЖДУ ХАРАКТЕРИСТИКАМИ ПОСТУПАТЕЛЬНОГО И ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
Между характеристиками вращательного и поступательного движения существует прямая аналогия, которая раскрывается в данном разделе.

Поступательное движение Вращательное движение

Мера положения тела

координаты x, y, z угловая координата .

Мера изменения положения тела

перемещение dr угловое перемещение d.

Мера быстроты изменения положения тела

скорость поступательного угловая скорость .

движения v

Мера быстроты изменения скорости

ускорение а угловое ускорение .

Мера внешнего воздействия

сила F момент силы М.

Мера количества движения

импульс р момент импульса L.

Мера инертности

масса m момент инерции J.

Основной закон динамики

F=ma M=J.

Кинетическая энергия

mv²/2 J²/2.

Работа

.