ЖАНСАЯ. 4дріс Фредгольм теориясы Жоспар
 Скачать 46.45 Kb. Скачать 46.45 Kb.
|
|
4-дәріс Фредгольм теориясы Жоспар Ерекшеленген ядролы Фредгольмнің 2-ші текті интегралдық теңдеуі. Фредгольмнің теориясы. Ерекшеленген ядро деп біреу тек  айнымалысына, ал екіншісі тек айнымалысына, ал екіншісі тек  айнымалысына тәуелді екі функция көбейтінділерінің ақырлы қосындысынан тұратын, яғни айнымалысына тәуелді екі функция көбейтінділерінің ақырлы қосындысынан тұратын, яғни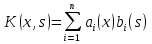 (1) (1)түріндегі ядро аталады. Жалпы жағдайда 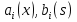 функциялары өзара сызықты тәуелсіз деп қараймыз. Егер олардың кейбіреулері сызықты тәуелді болса, онда (1) өрнегіндегі қосылғыштарды жинақтап, көбейткіштер сызықты тәуелсіз болатындай етіп түрлендіруге болады. функциялары өзара сызықты тәуелсіз деп қараймыз. Егер олардың кейбіреулері сызықты тәуелді болса, онда (1) өрнегіндегі қосылғыштарды жинақтап, көбейткіштер сызықты тәуелсіз болатындай етіп түрлендіруге болады.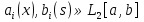 болсын. Бұл жағдайда болсын. Бұл жағдайда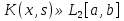 болады. болады.Фредгольмнің екінші текті 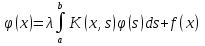 (2) (2)интегралдық теңдеуін қарастырайық. Егер 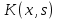 ядросын (1) өрнекпен аустырсақ, онда теңдеуден ядросын (1) өрнекпен аустырсақ, онда теңдеуден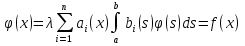 (3) (3)теңдеуі шығады. Бұл теңдеудің шешімі бар деп ұйғарайық. Егер 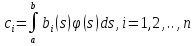  деп белгілесек, онда 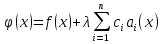 (4) (4)Сонымен (2) теңдеуінің шешімін табу мәселесі тұрақты 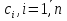 белгісіз коэффициенттерін анықтауға келтірілді. белгісіз коэффициенттерін анықтауға келтірілді.Егер (4) теңдеуінің екі жағында 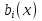 функцияларына көбейтіп, алынған өрнекті функцияларына көбейтіп, алынған өрнекті 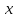 бойынша бойынша 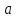 дан дан 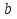 ға дейін интегралдасақ, ға дейін интегралдасақ, 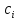 коэффициенттерін анықтайтын алгебралық сызықтық теңдеулер жүйесің коэффициенттерін анықтайтын алгебралық сызықтық теңдеулер жүйесің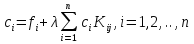 (5) (5)аламыз, мұндағы 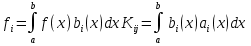 Әрине, осы алгебралық жүйенің шешімі жоқ болса, онда (3) интегралдық теңдеуінің де шешімі жоқ болады. Егер 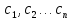 айнымалылар (5) жүйенің шешімдері бар болса, онда (4) теңдігінен айнымалылар (5) жүйенің шешімдері бар болса, онда (4) теңдігінен 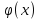 функциясының (3) теңдеуінің шешімі екенін тексеріп көру қиын емес. функциясының (3) теңдеуінің шешімі екенін тексеріп көру қиын емес.Ал (5) теңдеулер жүйенің шешімінің бар болуы белгісіз 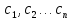 айнымалылардың коэффициенттерінең құралған анықтауышқа байланысты екені алгебра курсынан белгілі. Сондықтан айнымалылардың коэффициенттерінең құралған анықтауышқа байланысты екені алгебра курсынан белгілі. Сондықтан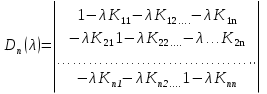 анықтауышын қарастырайық. Әрине 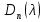 анықтауыш анықтауыш 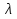 -ға байланысты -ға байланысты  дәрежелі көпмүшелік және дәрежелі көпмүшелік және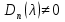 , себебі , себебі 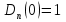 Демек, Демек, 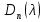 көпмүшелігінің түбірлерінің саны көпмүшелігінің түбірлерінің саны  нан артық болмайды. Ол түбірлерді нан артық болмайды. Ол түбірлерді 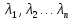 деп белгілейік. деп белгілейік.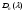 көпмүшелігі (3) теңдеу үшін Фредгольм анықтаушы, ал ол көпмүшеліктің түбірлері көпмүшелігі (3) теңдеу үшін Фредгольм анықтаушы, ал ол көпмүшеліктің түбірлері 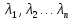 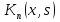 ядросының немесе (3) интегралдық теңдеуінің меншікті сандары деп аталады. Сызықтық алгебралық жүйелер теориясы бойынша ( ядросының немесе (3) интегралдық теңдеуінің меншікті сандары деп аталады. Сызықтық алгебралық жүйелер теориясы бойынша (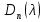 анықтаушы үшін) мына тұжырымдарға әкеледі. анықтаушы үшін) мына тұжырымдарға әкеледі.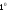 . Егер . Егер 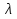 саны саны 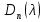 көпмүшелігінің түбірлерінің бір де біреуіне тең болмаса, онда кез келген көпмүшелігінің түбірлерінің бір де біреуіне тең болмаса, онда кез келген 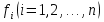 функциялары үшін (5) жүйенің жалғыз ғана шешімі бар болады. Демек, (2) интегралдық теңдеу үшін мына тұжырым орынды. функциялары үшін (5) жүйенің жалғыз ғана шешімі бар болады. Демек, (2) интегралдық теңдеу үшін мына тұжырым орынды.1-теорема. Егер 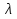 саны саны 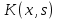 ядросының меншікті мәні болмаса, онда (3) интегралдық теңдеуінің кез келген ядросының меншікті мәні болмаса, онда (3) интегралдық теңдеуінің кез келген 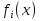 функция үшін (4) өрнегімен анықталатын жалғыз ғана функция үшін (4) өрнегімен анықталатын жалғыз ғана 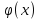 шешімі бар болады. шешімі бар болады. Әдетте бұл тұжырымды Фредгольмнің бірінші теоремасы дейді. 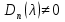 болса, біртекті алгебралық жүйенің шешімдері болса, біртекті алгебралық жүйенің шешімдері 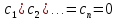 болады. Сондықтан болады. Сондықтан 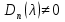 жағдайда біртекті интегралдық теңдеудің жағдайда біртекті интегралдық теңдеудің 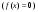 тек қана нольдік шешімі бар болады. тек қана нольдік шешімі бар болады.Егер (5) жүйесін Крамер әдісімен шешетін болсақ, онда алымындағы анықтауыштарды бос мүшесі орналасқан бағана элементтері бойынша жіктеп былай жазуға болады: 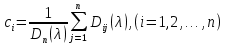 мұндағы 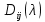 -алгебралық толықтауыштар, ол көрсеткіші -алгебралық толықтауыштар, ол көрсеткіші 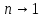 -ден аспайтын -ден аспайтын 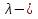 ға байланысты көпмүшелік. Белгісіз ға байланысты көпмүшелік. Белгісіз 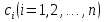 сандарының осы мәндерін (4) формулаға қойып, (3) теңдеуінің шешімін сандарының осы мәндерін (4) формулаға қойып, (3) теңдеуінің шешімін 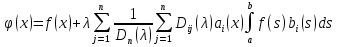 түрінде, немесе 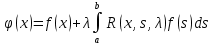 формуласымен анықтаймыз, мұнда 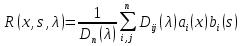 жоғарыдағы (3) интегралдық теңдеуінің резольвентасы шешу ядросы деп аталады. 2 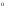 . Енді . Енді 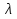 саны саны 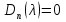 теңдеуі түбірлерінің біріне тең, яғни теңдеуі түбірлерінің біріне тең, яғни 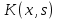 ядросының меншікті мәні болсын. Онда (1.5) жүйенің анықтауышы нольге тең. Бұл жағдайда сәйкес біртекті ядросының меншікті мәні болсын. Онда (1.5) жүйенің анықтауышы нольге тең. Бұл жағдайда сәйкес біртекті 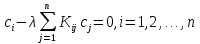 Жүйенің 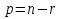 теңдеуі (мұнда теңдеуі (мұнда 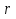 саны саны 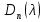 матрицасының рангі) сызықты тәуелсіз және нольге тең емес матрицасының рангі) сызықты тәуелсіз және нольге тең емес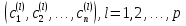 векторы оның шешімі болады. Ал сонда 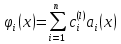 функциялары біртекті интегралдық 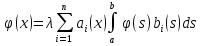 теңдеуінің нольге тең емес шешімдері болады. Бұл теңдеудің жалпы шешімі бұлай жазылады: 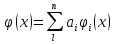 мұндағы 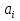 кез келген тұрақты шамалар. Біртекті интегралдық теңдеудің нольге тең емес шешімдерін сол теңдеудің меншікті мәндеріне сәйкес келетін меншікті функциялары деп атайды. кез келген тұрақты шамалар. Біртекті интегралдық теңдеудің нольге тең емес шешімдерін сол теңдеудің меншікті мәндеріне сәйкес келетін меншікті функциялары деп атайды.Енді (2) теңдеумен қатар мына 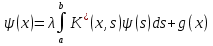 интегралдық теңдеуді қарастырайық, мұнда 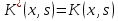 . Осы теңдеуді (2) интегралдық теңдеуіне түйіндес деп атайды. Ерекшеленген ядролы (3) интегралдық теңдеуіне түйіндес теңдеу . Осы теңдеуді (2) интегралдық теңдеуіне түйіндес деп атайды. Ерекшеленген ядролы (3) интегралдық теңдеуіне түйіндес теңдеу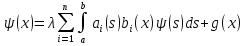 . .Бұл теңдеу үшін, (3) теңдеуіне айтылған тұжырымдарды сөзбе-сөз қайталауға болады. Онын шешімі 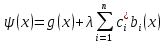 түрінде жазылады, мұнда 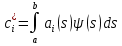 Егер 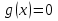 , яғни теңдеу біртекті болса, онда , яғни теңдеу біртекті болса, онда 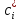 тұрақты коэффициенттерін сәйкес біртекті жүйеге түйіндес тұрақты коэффициенттерін сәйкес біртекті жүйеге түйіндес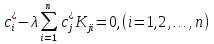 теңдеулер жүйесінен анықтаймыз. 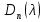 анықтауышы аталған жүйелерге ортақ болғандықтан сонғы жүйенен анықтауышы аталған жүйелерге ортақ болғандықтан сонғы жүйенен 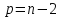 сызықты тәуелсіз вектор–шешімі бар болады: сызықты тәуелсіз вектор–шешімі бар болады: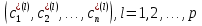 Сондықтан, 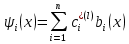 функциялары түйіндес біртекті интегралдық 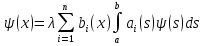 теңдеуінің шешімдері болады. Осыдан мынадай қорытынды шығады. 2-теорема. Егер 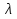 параметрі параметрі 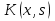 ядросының меншікті мәні болса, онда біртекті интегралдық теңдеумен оған түйіндес теңдеудің бірдей санды сызықты тәуелсіз меншікті функциялары бар болады. ядросының меншікті мәні болса, онда біртекті интегралдық теңдеумен оған түйіндес теңдеудің бірдей санды сызықты тәуелсіз меншікті функциялары бар болады.Бұл тұжырымды Фредгольмнің 2-теоремасы деп айтады. 3 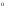 . Енді . Енді 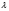 параметрі біртекті емес (3) интегралдық теңдеуінің меншікті мәні болған жағдайды қарастырайық. Жоғарыда айтқандай (3) теңдеуінің шешілуі (5) сызықтық теңдеулер жүйенің шешілуімен эквивалентті. Сондықтан, егер параметрі біртекті емес (3) интегралдық теңдеуінің меншікті мәні болған жағдайды қарастырайық. Жоғарыда айтқандай (3) теңдеуінің шешілуі (5) сызықтық теңдеулер жүйенің шешілуімен эквивалентті. Сондықтан, егер 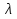 параметрі параметрі 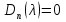 теңдеудің түбірі болса, онда (5) жүйе шешілмейді, демек, (3) интегралдық теңдеуінің шешімі жоқ болады. Ал егер теңдеудің түбірі болса, онда (5) жүйе шешілмейді, демек, (3) интегралдық теңдеуінің шешімі жоқ болады. Ал егер 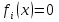 , яғни, , яғни,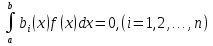 болса, онда (5) жүйенің шешімі бар. Демек, соңғы шарттар орындалған жағдайда (3) біртекті емес интегралдық теңдеуінің шешімі бар болады. Осы шаттарды жоғарыдағы қатарға қолдансақ, 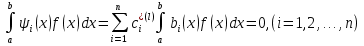 шарттарын аламыз. Сонымен мынадай теорема делелдедік. 3-теорема. Егер 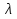 ядроның меншікті мәні болса, онда жалпы жағдайда (3) интегралдық теңдеуінің шешімі жоқ болады. Біртекті емес (3) интегралдық теңдеуінің шешімі бар болуы үшін ондағы бос мүше ядроның меншікті мәні болса, онда жалпы жағдайда (3) интегралдық теңдеуінің шешімі жоқ болады. Біртекті емес (3) интегралдық теңдеуінің шешімі бар болуы үшін ондағы бос мүше 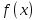 ол теңдеуге түйіндес біртекті теңдеудің сәйкес барлық шешімдеріне ортогоналды болуы қажетті де жеткілікті. ол теңдеуге түйіндес біртекті теңдеудің сәйкес барлық шешімдеріне ортогоналды болуы қажетті де жеткілікті.Бұл – Фредгольмнің үшінші теоремасы. Ал соңғы шарттар орындалған жағдайда (3) теңдеуінің ақырсыз көп шешімі бар болады: 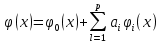 мұндағы 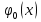 - біртекті емес интегралды теңдеудің жеке шешуі, ал - біртекті емес интегралды теңдеудің жеке шешуі, ал 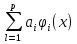 сәйкес біртекті теңдеудің жалпы шешуі. сәйкес біртекті теңдеудің жалпы шешуі.Ұсынылатын әдебиеттер 1. Орынбасаров, Ш. Сақаев. Интегралдық теңдеулер. Алматы «Білім» 1994. 2. Васильева А.Б., Тихонов А.Н. Интегральные уравнения М. 3. Краснов М.Л., Макаренко Г.И. Операционное исчисление. Устойчивость движения. Наука. 1964. 4. Краснов М.Л. Интегральные уравнения. М. 1975. 5. Лизоркин П.И. Курс дифференциальных и интегральных уравнений. М.1981. 6. Михлин С.Г. Лекции по линейным интегральным уравнениям. М. 1959. 7. Михлин С.Г. Приложения интегральных уравнений к некоторым проблемам механики, математической физики и техники. Гостехиздат. 194 |
