Высщая математика. 4 индивидуальные домашние задания 4Shaxsiy topshiriqlar Задания 1
 Скачать 365.89 Kb. Скачать 365.89 Kb.
|
|
4- индивидуальные домашние задания 4-Shaxsiy topshiriqlar Задания 1. Проверить, будут ли коллинеарны или ортогональны два 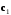 и и 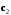 вектора которого образованы векторами вектора которого образованы векторами 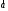 и и 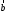 . .1-Topshiriq: 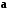 va va 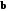 vektorlardan yasalgan vektorlardan yasalgan 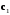 va va 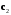 vektorlar kolline armi? vektorlar kolline armi?1. 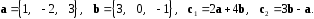 2. 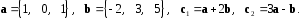 3. 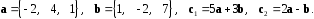 4. 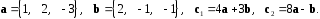 5. 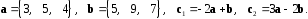 6. 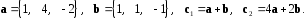 7. 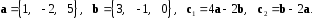 8. 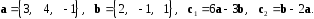 9. 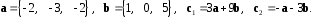 10. 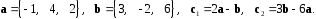 11. 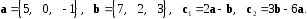 12. 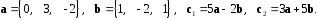 13. 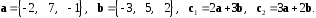 14. 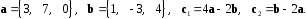 15. 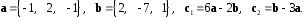 16. 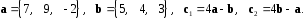 17. 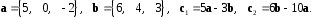 18. 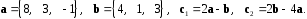 19. 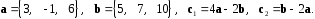 20. 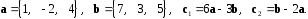 21. 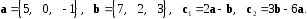 22. 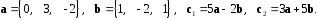 23. 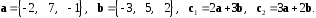 24. 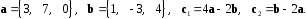 25. 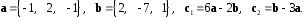 26. 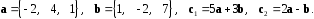 27. 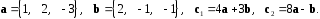 28. 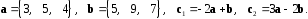 29. 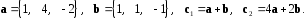 30. 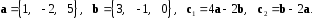 Задания 2. Определить в декартовой системе координат угол между вектором 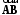 и вектором и вектором 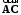 . .2-Topshiriq: 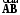 va va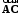 vektorlar orasidagi burchak kosinusini toping. vektorlar orasidagi burchak kosinusini toping.1. 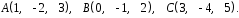 2. 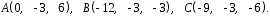 3. 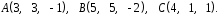 4. 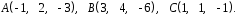 5. 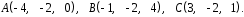 6. 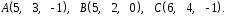 7. 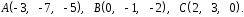 8. 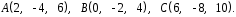 9. 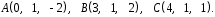 10. 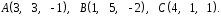 11. 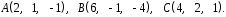 12. 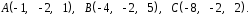 13. 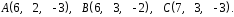 14. 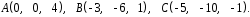 15. 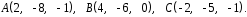 16. 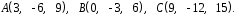 17. 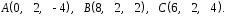 18. 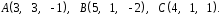 19. 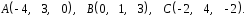 20. 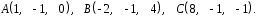 21. 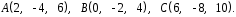 22. 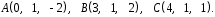 23. 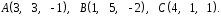 24. 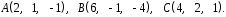 25. 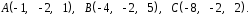 26. 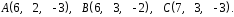 27. 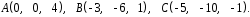 28. 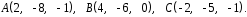 29. 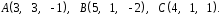 30. 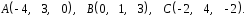 Задания 3. Вычислить площадь параллелограмма, две стороны которого образованы векторами 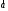 и и 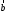 , ,3-Topshiriq: 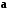 va va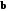 vektorlarga qurilgan parallelogramm yuzini toping. vektorlarga qurilgan parallelogramm yuzini toping. 1. 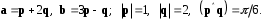 2. 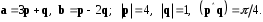 3. 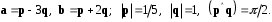 4. 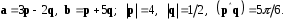 5. 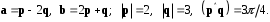 6. 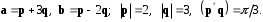 7. 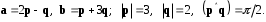 8. 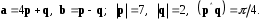 9. 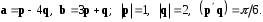 10. 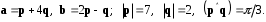 11. 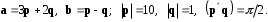 12. 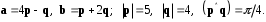 13. 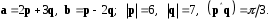 14. 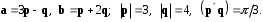 15. 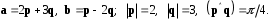 16. 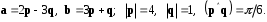 17. 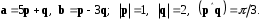 18. 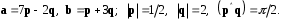 19. 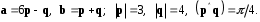 20. 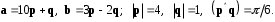 21. 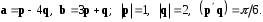 22. 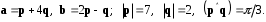 23. 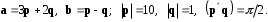 24. 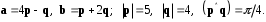 25. 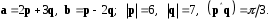 26. 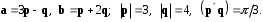 27. 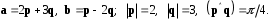 28. 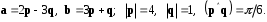 29. 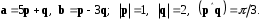 30. 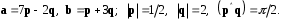 Задания 4. 4-Topshiriq: Написать разложение вектораx по векторам p, q, r. x vektorini p, q, r vektorlar orqali yoying 3.1 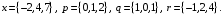 3.2 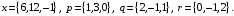 3.3 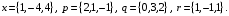 3.4 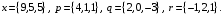 3.5 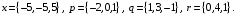 3.6 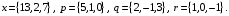 3.7 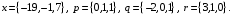 3.8 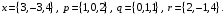 3.9 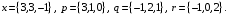 3.10 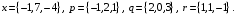 3.11 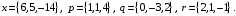 3.12 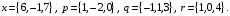 3.13 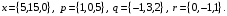 3.14 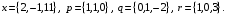 3.15 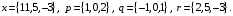 3.16 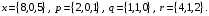 3.17 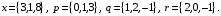 3.18 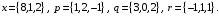 3.19 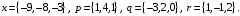 3.20 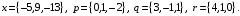 3.21 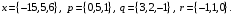 3.22 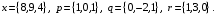 3.23 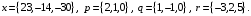 3.24 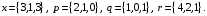 3.25 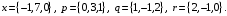 3.26 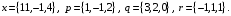 3.27 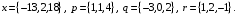 3.28 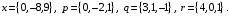 3.29 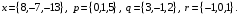 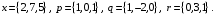 Задания 5. Доказать, что векторы 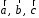 образуют базис, и найти координаты вектора образуют базис, и найти координаты вектора 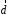 в этом базисе. в этом базисе.5-Topshiriq: 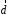 vektorning vektorning 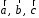 vektorlar orqali yoyilmasini toping. vektorlar orqali yoyilmasini toping.Найдите разложение вектора 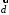 по векторам по векторам 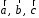 . .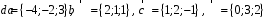 ; ;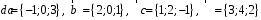 ; ;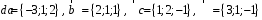 ; ;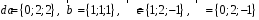 ; ;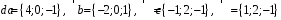 ; ;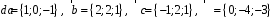 ; ;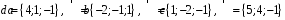 ; ;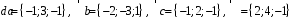 ; ;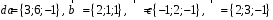 ; ;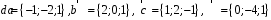 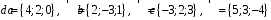 ; ;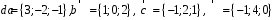 ; ;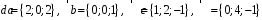 ; ;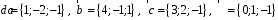 ; ;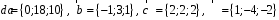 ; ;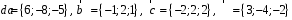 ; ;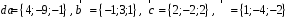 ; ;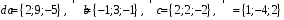 ; ;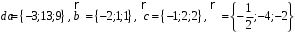 ; ;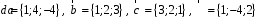 ; ;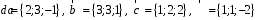 ; ;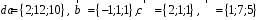 ; ;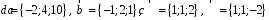 ; ;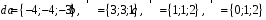 ; ;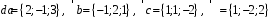 ; ;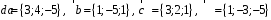 ; ; ; ; ; ; ; ;5.30  . .Задания 6. 6-Topshiriq: Даны координаты точек:  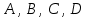 . .Найти: 1) длину вектора 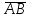 , ,2) угол между векторами 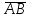 и и 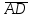 , ,3) площадь треугольника 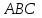 , ,4) объём пирамиды 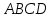 , ,1. A (5, 1, 4 ); B (-7, 6, 5 ); C (3, -4, 3 ); D (0, 2, 9 ). 2. A (5, 2, 0 ); B (2, 5, 0 ); C (1, 2, 4 ); D (-1, 1, 1 ). 3. A (-2, 0, -4 ); B (-1, 7, 1 ); C (4, -8, -4 ); D (1, -4, 6 ). 4. A (2, -1, 2 ); B (1, 2, -1 ); C (3, 2, 1 ); D (-4, 2, 5 ). 5. A (-1, 2, -3 ); B (4, -1, 0 ); C (2, 1, -2 ); D (3, 4, 5 ). 6. A (1, -1, 1 ); B (-2, 0, 3 ); C (2, 1, -1 ); D (2, -2, -4 ). 7. A (1, 2, 0 ); B (1, -1, 2 ); C (0, 1, -1 ); D (-3, 0, 1 ). 8. A (1, 0, 2 ); B (1, 2, -1 ); C (2, -2, 1 ); D (2, 1, 0 ). 9. A (1, 3, 0 ); B (4, -1, 2 ); C (3, 0, 1 ); D (-4, 3, 5 ). 10. A (0, 3, 2 ); B (-1, 3, 6 ); C (-2, 4, 2 ); D (0, 5, 4 ). 11. A (5, 2, 0 ); B (2, 5, 0 ); C (1, 2, 4 ); D (-1, 1, 1 ). 12. A (2, -1, 2 ); B (1, 2, -1 ); C (3, 2, 1 ); D (-4, 2, 5 ). 13. A (1, -1, 1 ); B (-2, 0, 3 ); C (2, 1, -1 ); D (2, -2, -4 ). 14. A (1, 0, 2 ); B (1, 2, -1 ); C (2, -2, 1 ); D (2, 1, 0 ). 15. A (0, 3, 2 ); B (-1, 3, 6 ); C (-2, 4, 2 ); D (0, 5, 4 ). 16. A (1, 3, 0 ); B (4, -1, 2 ); C (3, 0, 1 ); D (-4, 3, 5 ). 17. A (1, 2, 0 ); B (1, -1, 2 ); C (0, 1, -1 ); D (-3, 0, 1 ). 18. A (-1, 2, -3 ); B (4, -1, 0 ); C (2, 1, -2 ); D (3, 4, 5 ). 19. A (-2, 0, -4 ); B (-1, 7, 1 ); C (4, -8, -4 ); D (1, -4, 6 ). 20. A (5, 1, 4 ); B (-7, 6, 5 ); C (3, -4, 3 ); D (0, 2, 9 ). 21. A (1, -1, 1 ); B (-2, 0, 3 ); C (2, 1, -1 ); D (2, -2, -4 ). 22. A (1, 2, 0 ); B (1, -1, 2 ); C (0, 1, -1 ); D (-3, 0, 1 ). 23. A (1, 0, 2 ); B (1, 2, -1 ); C (2, -2, 1 ); D (2, 1, 0 ). 24. A (1, 3, 0 ); B (4, -1, 2 ); C (3, 0, 1 ); D (-4, 3, 5 ). 25. A (0, 3, 2 ); B (-1, 3, 6 ); C (-2, 4, 2 ); D (0, 5, 4 ). 26. A (5, 1, 4 ); B (-7, 6, 5 ); C (3, -4, 3 ); D (0, 2, 9 ). 27. A (5, 2, 0 ); B (2, 5, 0 ); C (1, 2, 4 ); D (-1, 1, 1 ). 28. A (-2, 0, -4 ); B (-1, 7, 1 ); C (4, -8, -4 ); D (1, -4, 6 ). 29. A (2, -1, 2 ); B (1, 2, -1 ); C (3, 2, 1 ); D (-4, 2, 5 ). 30. A (-1, 2, -3 ); B (4, -1, 0 ); C (2, 1, -2 ); D (3, 4, 5 ). Задания 7. 7-Topshiriq: При каком 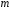 , если оно существует, векторы , если оно существует, векторы 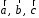 компланарны? компланарны?4. 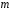 ning qanday qiymatida ning qanday qiymatida 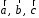 vektorlar chiziqli bog’liq bo‘ladi? vektorlar chiziqli bog’liq bo‘ladi? При каком значении параметра 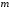 векторы векторы 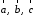 будут линейно зависимыми? будут линейно зависимыми?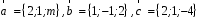 ; ;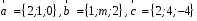 ; ;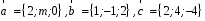 ; ;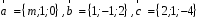 ; ;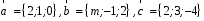 ; ;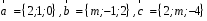 ; ;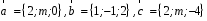 ; ;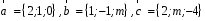 ; ;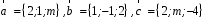 ; ;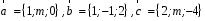 ; ;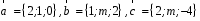 ; ;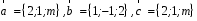 ; ;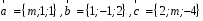 ; ;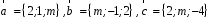 ; ;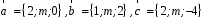 ; ;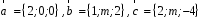 ; ;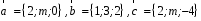 ; ;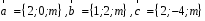 ; ;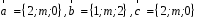 ; ;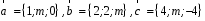 ; ;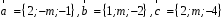 ; ;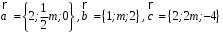 ; ;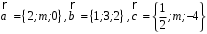 ; ;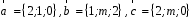 ; ;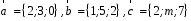 ; ;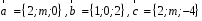 ; ;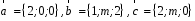 ; ;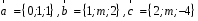 ; ;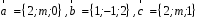 ; ;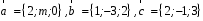 . .Задания 8. 8-Topshiriq: Для векторов 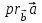 и и 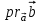 в декартовой системе координат. в декартовой системе координат.2 |
