Расчёт замкнутой сети. №4 - Расчет замкнутой сети. 4. расчет замкнутой сети распределение потоков мощности и напряжений в простых замкнутых сетях

• Название: 4. расчет замкнутой сети распределение потоков мощности и напряжений в простых замкнутых сетях
• Анкор: Расчёт замкнутой сети
• Дата: 27.04.2021
• Размер: 430.5 Kb.
• Имя файла: №4 - Расчет замкнутой сети.doc
• Тип: Документы; #199419

№4. РАСЧЕТ ЗАМКНУТОЙ СЕТИ

4. РАСПРЕДЕЛЕНИЕ ПОТОКОВ МОЩНОСТИ И НАПРЯЖЕНИЙ
В ПРОСТЫХ ЗАМКНУТЫХ СЕТЯХ

Ранее рассматривались разомкнутые сети. Ниже будут рассматриваться замкнутые сети. Напомним, что в разомк­нутых сетях все узлы получают питание только по одной
ветви.

В простых замкнутых сетях есть узлы, питающиеся по двум ветвям, но нет узлов, получающих питание более чем по двум ветвям, отсутствуют узлы, с которыми соединены три и более ветви (рис. 3.14, а, б). Простые замкнутые сети содержат только один контур.


Рис. 3.13. Примеры простых разом-
кнутых сетей:

а — неразветвленной; б — разветвлен-
ной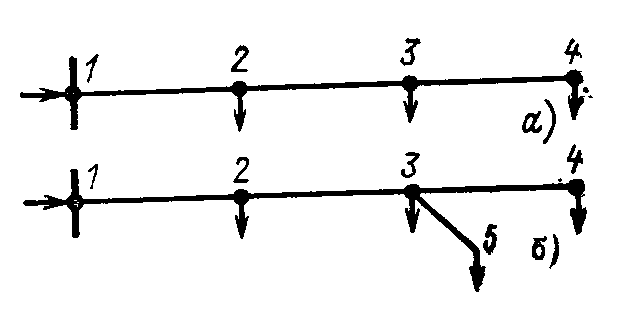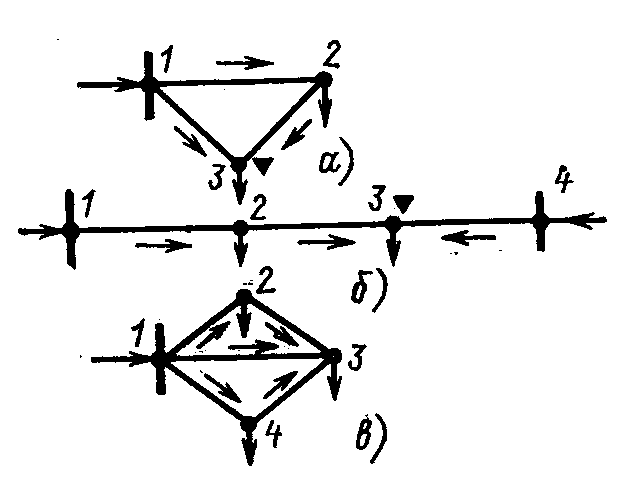


Рис. 3.14. Примеры простых замкнутых сетей:

а — треугольник; б — линия с двусторонним питанием; в — сложнозамкнутая сеть


Характерным частным видом простой замкнутой сети является кольцевая сеть (рис. 3.14, а). Она содержит один замкнутый контур. В качестве источников питания могут служить или электростанции, или шины подстанций, в свою очередь связанные сетью с электростанциями системы.
Кольцевая сеть на рис. 3.14, а может быть представлена в виде линии с двухсторонним питанием (рис. 3.14, б). Действительно, если источник питания в узле 1 мысленно раз­делить на два и представить в виде узлов 1 и 4, то из коль­цевой сети на рис. 3.14, а получим линию с двухсторонним питанием на рис. 3.14,б.

В сложной замкнутой сети есть узел, с которым соеди­нены три ветви или более (рис 3.14, в). Сложная замкну­тая сеть содержит два и более контуров.

К достоинствам замкнутых сетей следует отнести по­вышенную надежность электроснабжения потребителей, меньшие потери мощности, к недостаткам — сложность эксплуатации, удорожание за счет дополнительных линий. Расчеты замкнутых сетей сложнее, чем разомкнутых.

Распределение потоков мощности в простой замкнутой сети без учета потерь мощности. Представим простейшую замкнутую сеть в виде линии с двухсторонним питанием
( рис. 3.15, а) и рассмотрим различные случаи.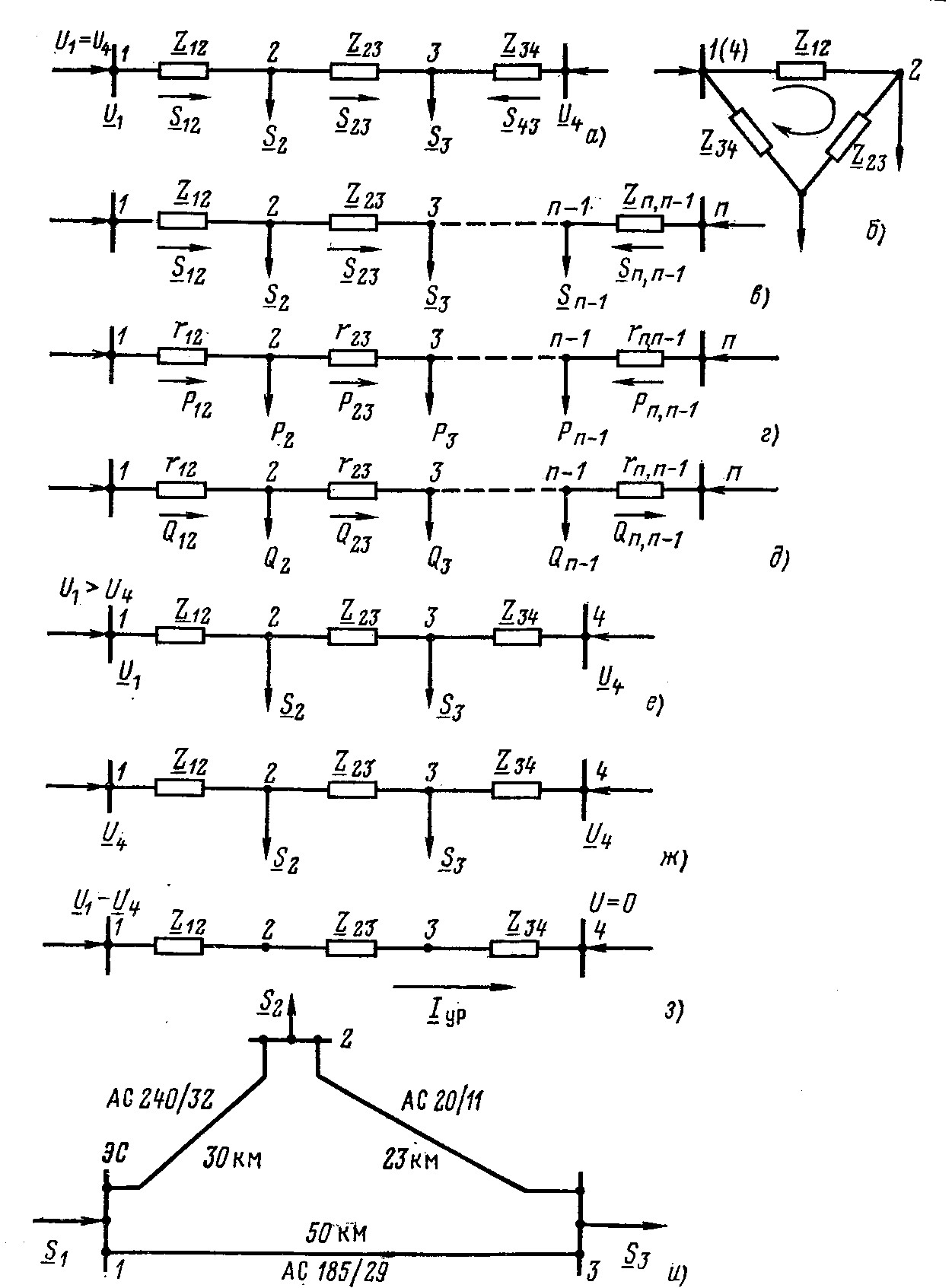



Рис. 3.15. Распределение потоков мощности в линии с двухсторонним питанием без учета потерь мощности:

а—схема замещения линии с четырьмя узлами; б—иллюстрация второго закона Кирхгофа; в—линия с п узлами; г,д—распределение Р и в однородной линии; е—линия с четырьмя узлами при ; ж, з—эквивалентное представление линии на рис, е; и—схема кольцевой сети 110 кВ
Заданы одинаковые напряжения по концам линии . Известны мощности нагрузки , , сопротивления участков линии , где k. — узел начала участка линии; j — узел конца.

Принимаем следующие допущения:

а) пренебрегаем потерями мощности при опреде­лении потоков ;

б) предполагаем, что ток участка определяется по но­минальному напряжению:

;

в) используем расчетные мощности нагрузок под­станции.

При равенстве напряжений источников питания на ос­новании второго закона Кирхгофа можно записать (рис. 3.15,б)

.

Если заменим в последнем выражении все комплексные величины на сопряженные, то получим следующее урав­нение:

. (3.70)

Так как потери мощности не учитываются, первый за­кон Кирхгофа для узлов 2 и 3 можно записать так:

; (3.71)

. (3.72)

Подставив значения мощностей (3.71) и (3.72) в урав­нение (3.70), получим уравнение с одним неизвестным:

.

Отсюда находим значение потока мощности :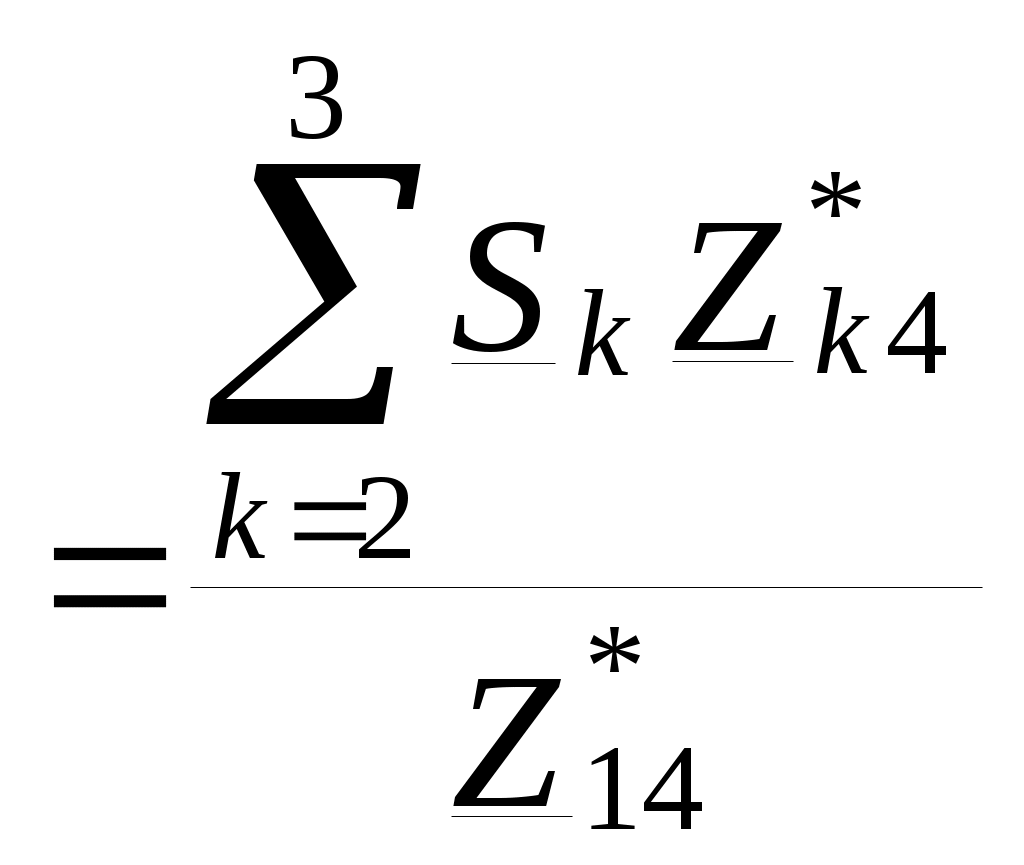



, (3.73)

где

.

Аналогично можно вывести формулу для определения потока мощности :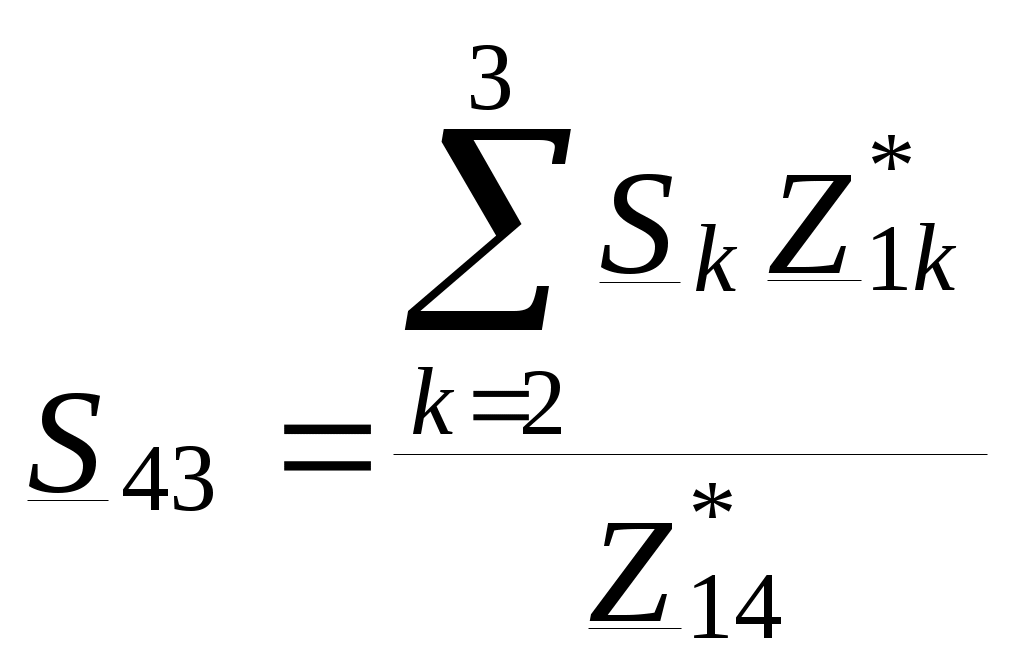

, (3.74)

где .

Значение потока мощности можно легко найти на основании первого закона Кирхгофа из (3.71).

Кольцевая сеть (рис. 3.15, и) напряжением ...... кВ свя­зывает электростанцию 1 с понижающими подстанциями 2, 3, имеющими расчетные нагрузки , МВА и , МВА. Марки проводов, длины линий указаны. Выбрать сечения проводов и подсчитать их со­противления и проводимости, зарядную мощность. Напряжение на шинах электростанции, …..кВ. Определить мощность, которая поступает с шин электростанции. Расчет проведем с учетом потерь мощности.

РЕШЕНИЕ. Составим схему замещения сети в виде линии с двухсторонним питанием, разрезая кольцо в узле 1 (рис. 3.15,а). Определим по выраже­ниям (3.73) и (3.74) приближенное потокораспределение в кольце с целью выявления точки потокораздела:



МВА;



МВА.

Проверим правильность определения потоков мощности на головных линиях кольца по условию :

Значения и определены верно. Находим поток мощности в линии 23 по первому закону Кирхгофа для узла 2:

МВА.

Узел 3 — точка потокораздела активной и реактивной мощности.
Мощность, поступающая с шин электростанции и определенная без уче­та потерь мощности, равна

МВА.

При одинаковом сечении проводов вдоль всей линии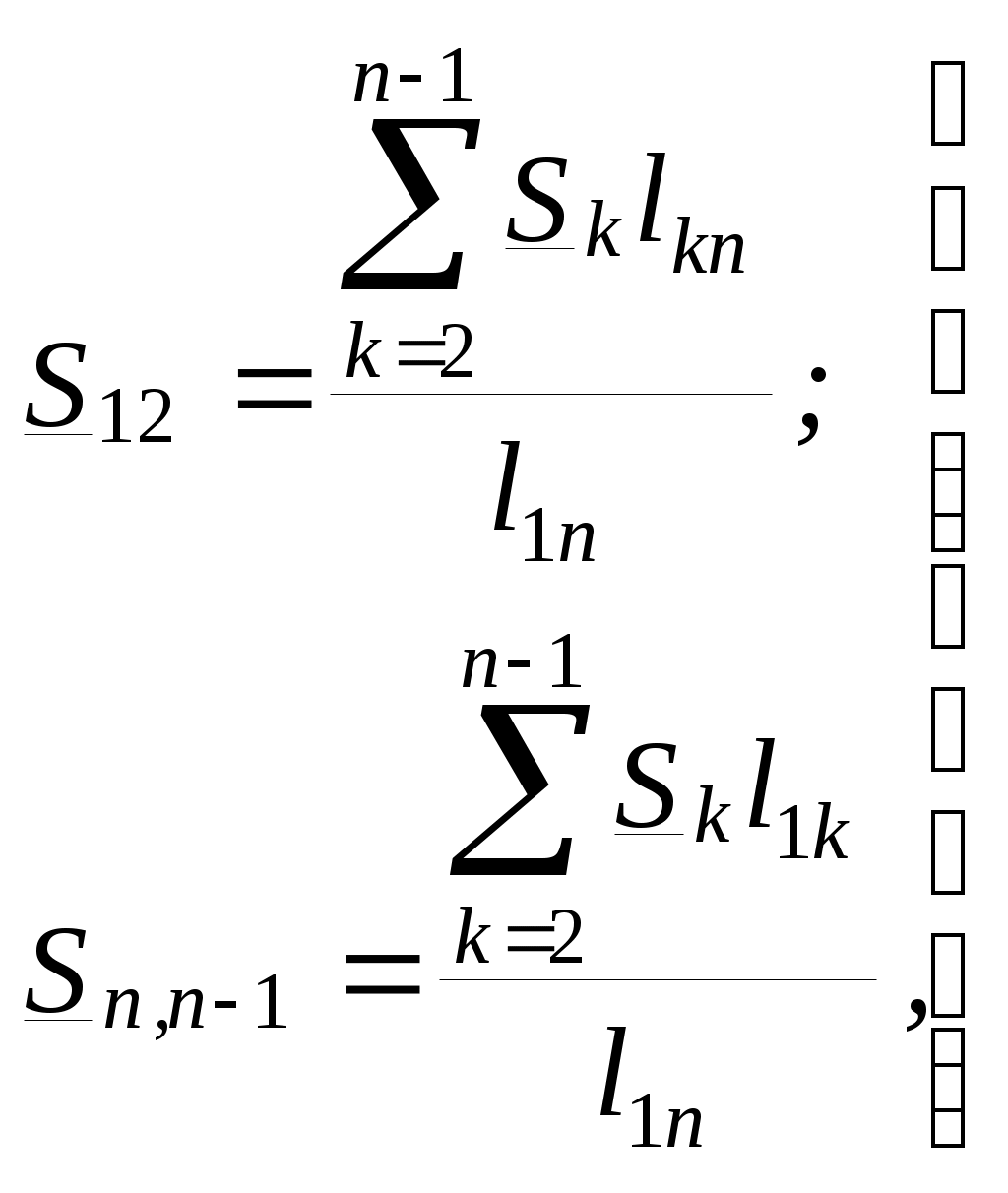

(3.80)

где , , — длины участков линии между узлами со­ответственно k и п, 1 и k, 1 и n.

В этом случае кольцевая сеть для дальнейшего расчета может быть также разделена на две разомкнутые линии. Вычислим предварительно потери мощности на участке
между точками потокораздела: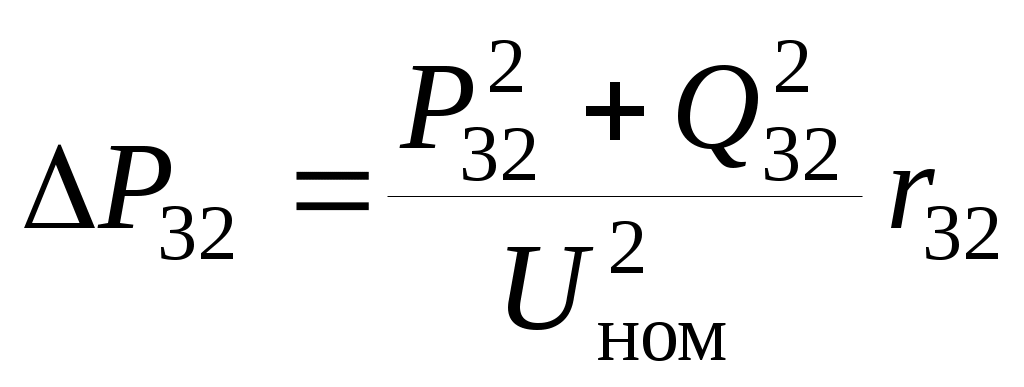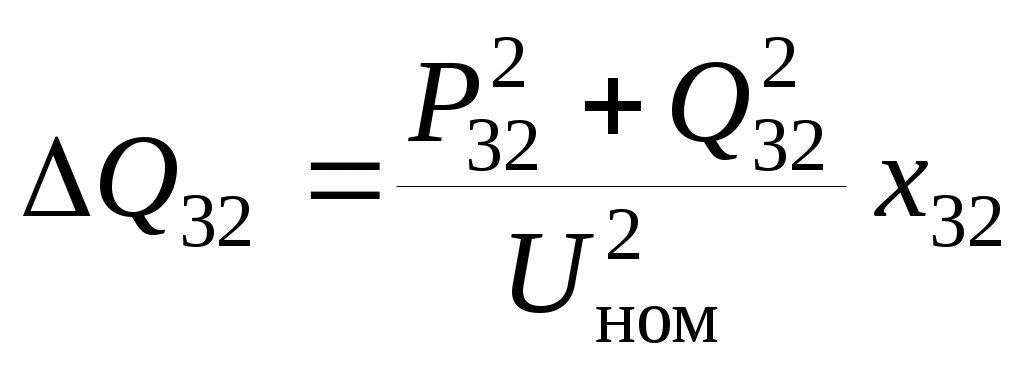

; .

Расчет с учетом потерь мощности. Рассмотрим линию
с двухсторонним питанием, к которой преобразуется прос­тая замкнутая сеть (рис. 3.16, а). Мощности , ,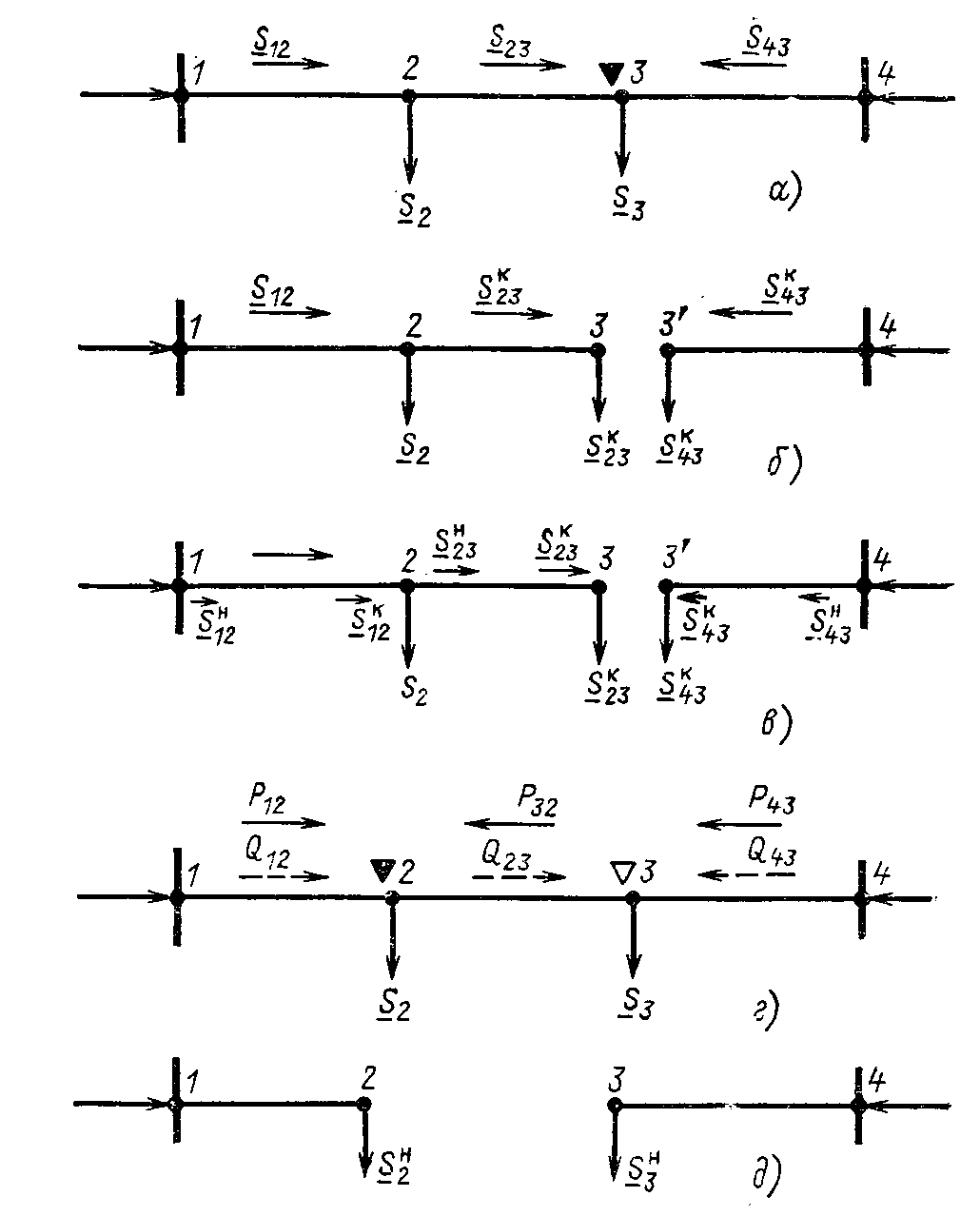

Рис. 3.16. Распределение потоков мощности в замкнутой сети с учетом потерь мощности:

а—исходная сеть; б—представление исходной сети в виде двух линий; в—услов­ные обозначения для расчета потоков в линиях с учетом потерь мощности; г—на­правления потоков в случае несовпадения точек потокораздела активной и реак­тивной мощностей; д—разделение сети при несовпадающих точках потокораздела
определим сначала без учета потерь по выражениям (3.73), (3.74), (3,71). Предположим, что направления мощностей соответствуют точке потокораздела в узле 3, который от­мечен залитым треугольником. «Разрежем» линию в узле 3 (рис. 3.16, б) и рассчитаем потоки мощности в линиях 13 и 43', как это делалось для разомкнутых сетей.

На участке 23 потери активной мощности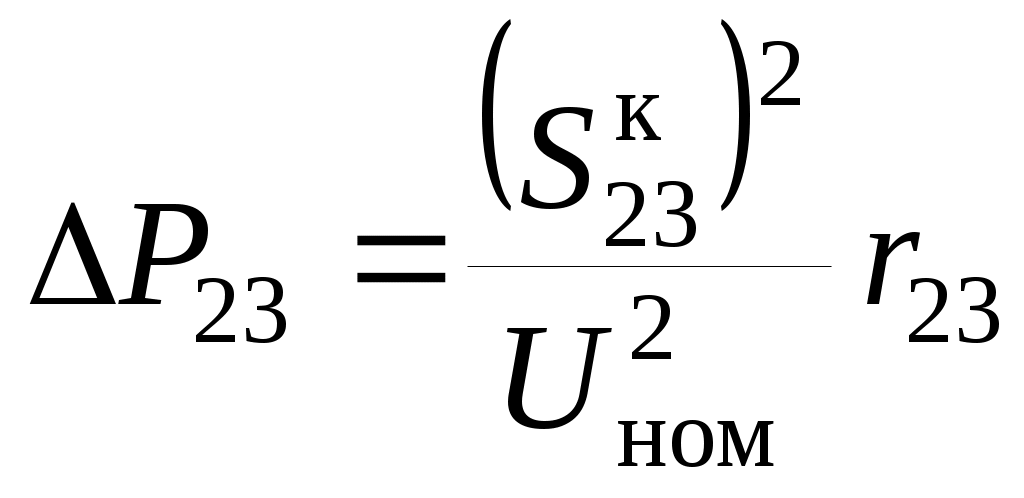

;

потери реактивной мощности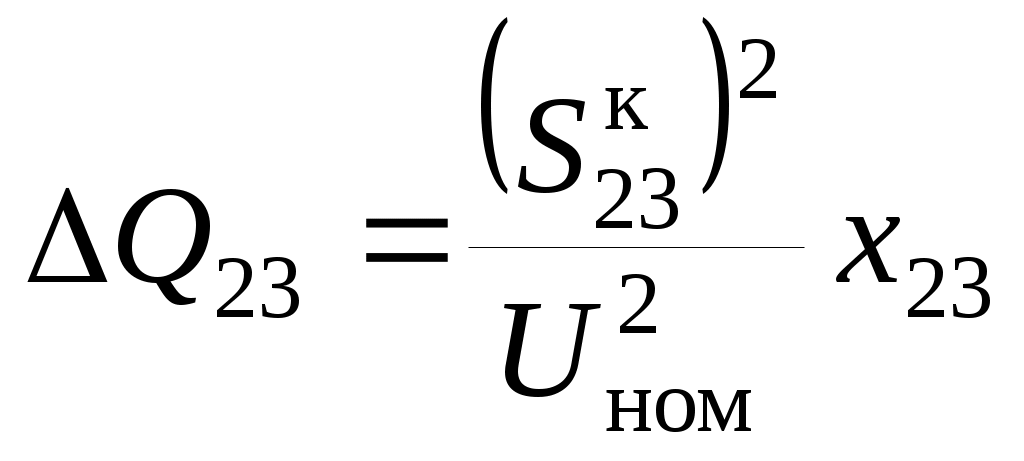

,

потери полной мощности

.

Находим значение потока мощности в начале участка 23 (рис, 3.16,в):

.

Далее расчет потоков мощности на участке 12 проводится как для разомкнутых сетей (1-й этап в § 3.6).

Может оказаться, что 1-й этап расчета кольцевой сети выявит две точки потокораздела: одну — для активной, а другую — для реактивной мощности. Такой случай ил­люстрируется на рис. 3.16, г, где узел 2—точка потоко­раздела для активной, а узел 3 — для реактивной мощ­ности.

В этом случае кольцевая сеть для дальнейшего расчета может быть также разделена на две разомкнутые линии. Вычислим предварительно потери мощности на участке между точками потокораздела: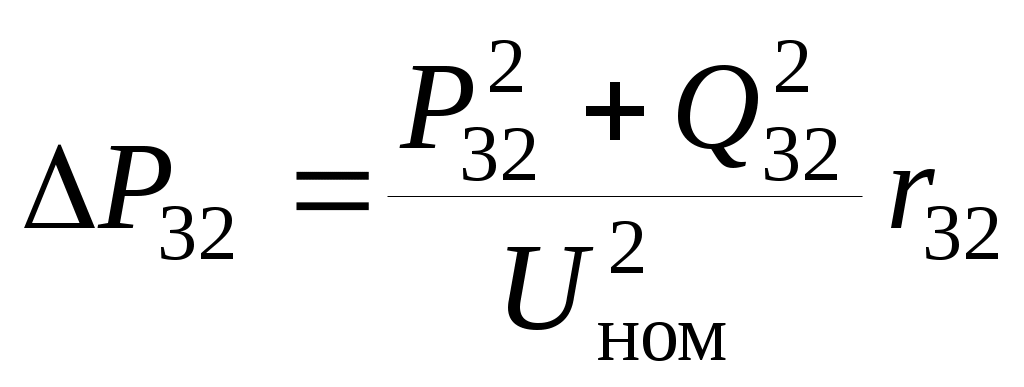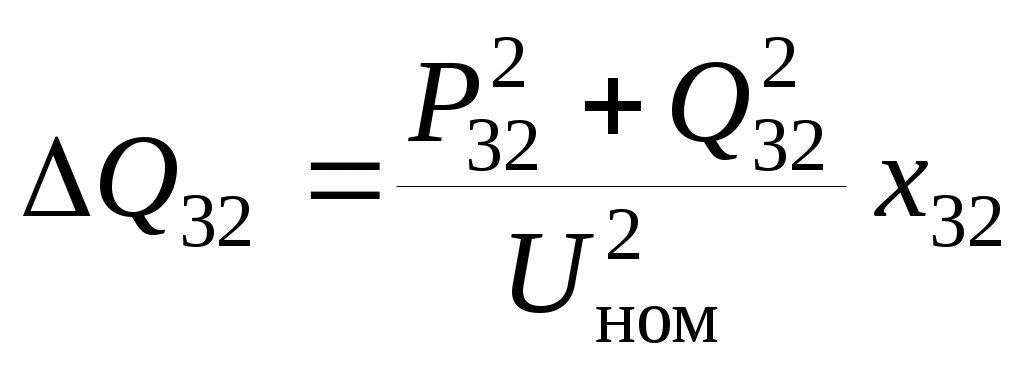

; .

Если теперь принять, что в точке 2 включена нагрузка

,

а в точке 3 — нагрузка

.

где , , , определяются по (3.73), (3.74), а , —по (3.71), то при дальнейшем расчете можно вместо кольцевой схемы рассматривать две разомкнутые линии, показанные на рис. 3.16, д.

«Разрежем» линию с двухсторонним питанием в узле 3 потокораздела, как на рис. 3.16,б. Нагрузки в узлах 3 и 3' равны МВА , МВА . Рассчитаем потоки мощности в линиях 23, 12 (рис. 3.16, в).

Мощность в конце линии 23 МВА. Потери мощности в линии 23

МВА.

Мощность в конце линии 12



МВА.

Потери мощности в линии 12

МВА.

Мощность в начале линии 12 .

МВА.

Рассчитаем потоки мощности в линии 43 (рис. 3.16,е). Мощность в конце линии 43 МВА. Потери мощности в ли­нии 43

МВА.

Мощность в начале линии 43

МВА.

Мощность, потребляемая с шин электростанции,

МВА.
№4. ЗАДАНИЕ. РЕШЕНИЕ.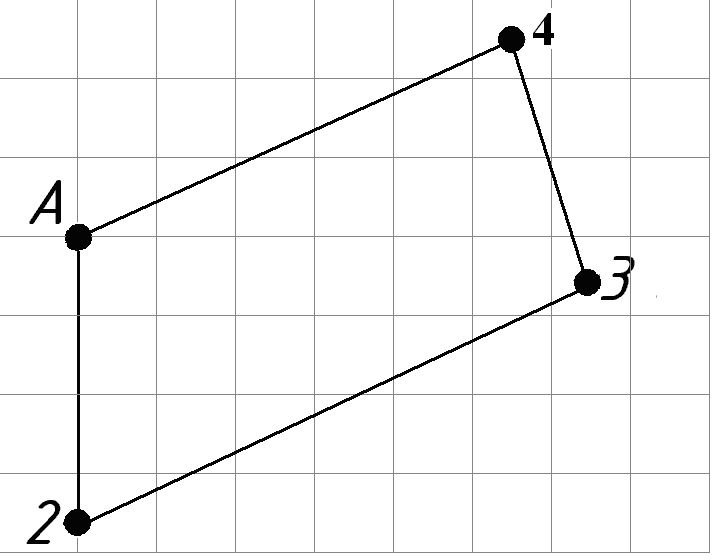


1) Для подстанции №2 : - определить активную мощность, а затем реактивную мощность через tgφ или .

2) «Разрежем» линию с двухсторонним питанием в узле А.

3) Определим по выраже­нию (3.80) приближенное потокораспределение в кольце с целью выявления точки потокораздела:

,МВА;

,МВА.

Проверим правильность определения потоков мощности на головных линиях кольца по условию :

значения и определены верно, если условие выполняется.

4) Находим поток мощности в линии 23 по первому закону Кирхгофа для узла 2:

МВА.
5) Находим поток мощности в линии 43 по первому закону Кирхгофа для узла 4:

МВА.

Узлы 2 или 3 — точка потокораздела активной и реактивной мощности.
6) Определим токи по участкам: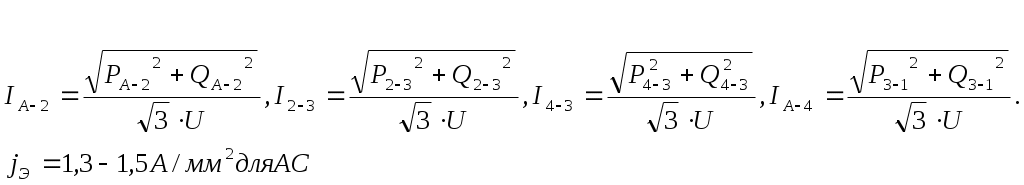



7)Определим сечение по экономической плотности тока:

и так для всех участков.

8) Выбираем по справочнику провода (по коронированию), данные провода записываем по участкам, определяем
Участок А-2 и так для всех участков.


9) Определяем параметры линии по участкам
Участок А-2 и так для всех участков.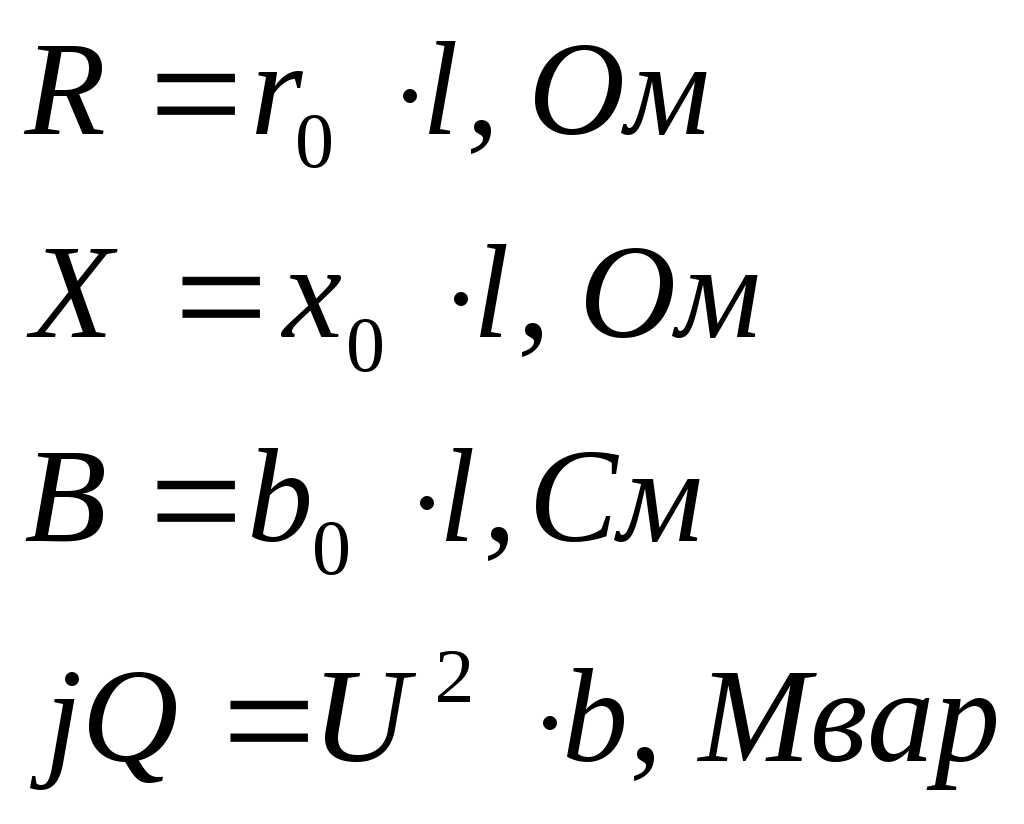


10) Произведем расчёт мощностей в режиме максимальных нагрузок
Участок 3-1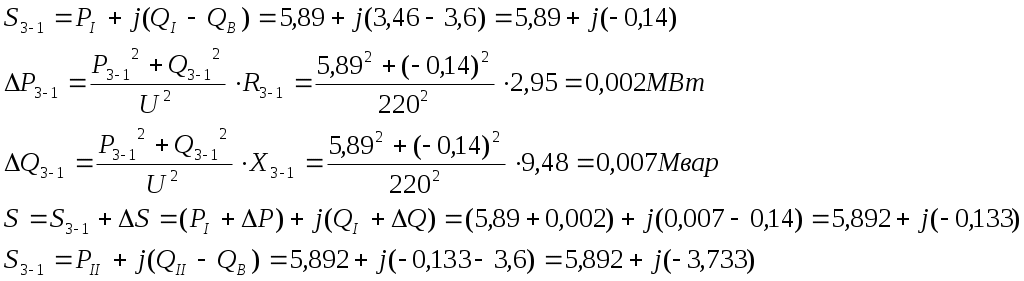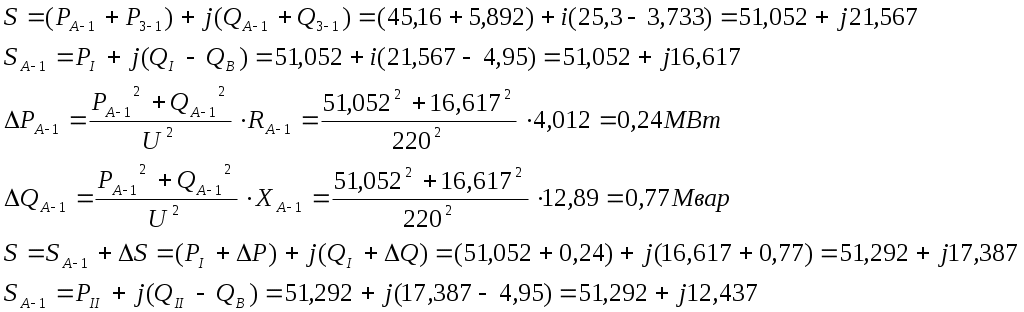



Участок А-1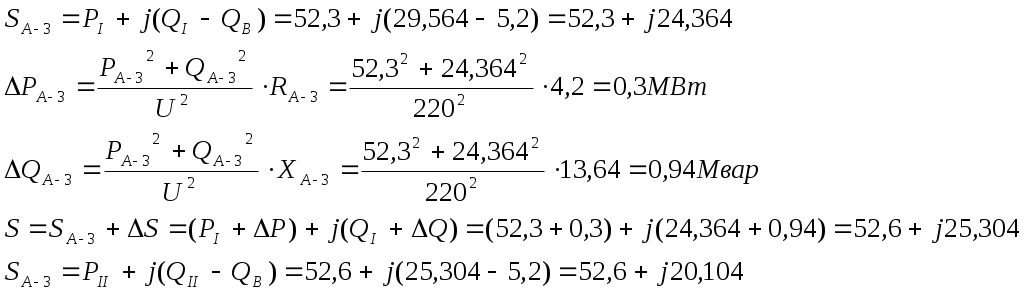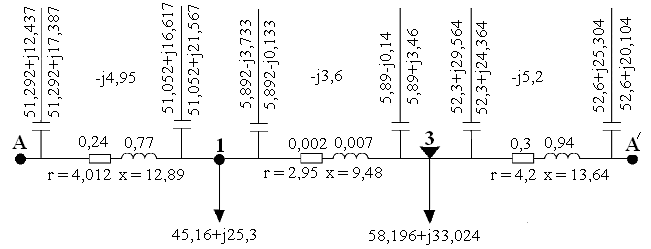


Участок А-3




11) Определение напряжения на шинах подстанции на высокой стороне.

Напряжение в ЦП: Umax=232кВ.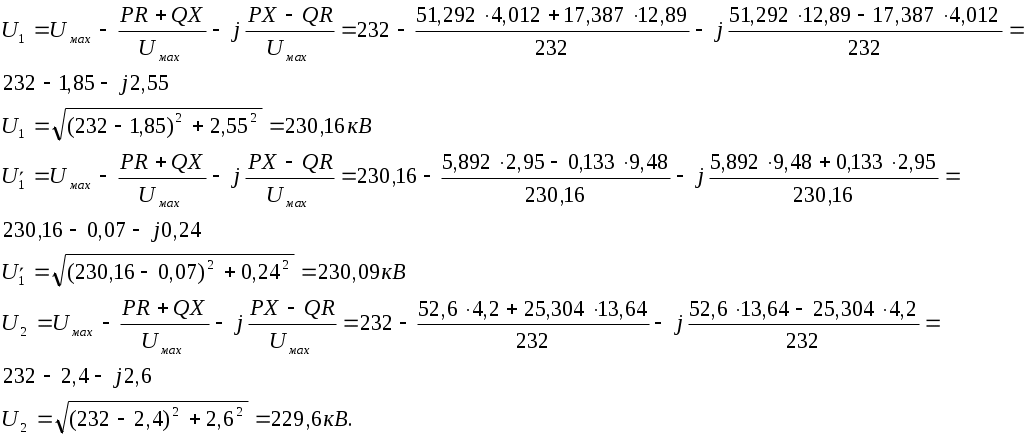




Пример 1. Мощности нагрузок на стороне ВН трансформаторов =280 МВА, =320 МВА, =380 МВА, линий длиной 200, 160, 235 км. Соs φ=0,91. Напряжение в ЦП 545 кВ.

Пример 2. Мощности нагрузок на стороне ВН трансформаторов =70 МВА, =100 МВА, =90 МВА, линий длиной 60, 50, 80 км. Соs φ=0,92. Напряжение в ЦП 239 кВ.

Пример 3. Мощности нагрузок на стороне ВН трансформаторов =75 МВА, =70 МВА, =65 МВА, линий длиной 49, 78, 60 км. Соs φ=0,93. Напряжение в ЦП 242 кВ.

Пример 4. Мощности нагрузок на стороне ВН трансформаторов =32 МВА, =18 МВА, =20 МВА, линий длиной 14, 26, 20 км. Соs φ=0,94. Напряжение в ЦП 119 кВ.

Пример 5. Мощности нагрузок на стороне ВН трансформаторов =28 МВА, =24 МВА, =21 МВА, линий длиной 15, 22, 10 км. Соs φ=0,95. Напряжение в ЦП 118 кВ.

Пример 6. Мощности нагрузок на стороне ВН трансформаторов =20 МВА, =26 МВА, =10 МВА, линий длиной 30,18,22 км. Соs φ=0,96. Напряжение в ЦП 117 кВ.

Пример 7. Мощности нагрузок на стороне ВН трансформаторов =70 МВА, =62 МВА, =96 МВА, линий длиной 45, 75, 60 км. Соs φ=0,89. Напряжение в ЦП 229 кВ.

Пример 8. Мощности нагрузок на стороне ВН трансформаторов =84 МВА, =74 МВА, =86 МВА, линий длиной 90, 60, 50 км. Соs φ=0,79. Напряжение в ЦП 239 кВ.

Пример 9. Мощности нагрузок на стороне ВН трансформаторов =120 МВА, =70 МВА, =88 МВА, линий длиной 85, 57, 74 км. Соs φ=0,88. Напряжение в ЦП 238 кВ.

Пример 10. Мощности нагрузок на стороне ВН трансформаторов =96 МВА, =209 МВА, =160 МВА, линий длиной 120, 95, 100 км. Соs φ=0,87. Напряжение в ЦП 351 кВ.

Пример 11. Мощности нагрузок на стороне ВН трансформаторов =182 МВА, =148 МВА, =226 МВА, линий длиной 105, 85, 120 км. Соs φ=0,86. Напряжение в ЦП 350 кВ.

Пример 12. Мощности нагрузок на стороне ВН трансформаторов =16, =22, =20 МВА, линий длиной 20 км, 15км, 12км. Соs φ=0,85. Напряжение в ЦП 121 кВ.

Пример13. Мощности нагрузок на стороне ВН трансформаторов =138МВА, =179 МВА, =106 МВА, линий длиной 100 км,80км, 75км. Соs φ=0,90. Напряжение в ЦП 348 кВ.

Пример 14. Мощности нагрузок на стороне ВН трансформаторов =182 МВА, =219 МВА, =316 МВА, линий длиной 100,180, 200 км. Соs φ=0,84. Напряжение в ЦП 550 кВ.

Пример 15. Мощности нагрузок на стороне ВН трансформаторов =232 МВА, =319 МВА, =416 МВА, линий длиной 240, 125, 190 км. Соs φ=0,83. Напряжение в ЦП 540 кВ.

Пример 16. Мощности нагрузок на стороне ВН трансформаторов =332 МВА, =419 МВА, =266 МВА, линий длиной 100, 165, 125 км. Соs φ=0,82. Напряжение в ЦП 543 кВ.

Пример 17. Мощности нагрузок на стороне ВН трансформаторов =54 МВА, =80 МВА, =70 МВА, линий длиной 50, 60, 85км. Соs φ=0,81. Напряжение в ЦП 233 кВ.

Пример 18. Мощности нагрузок на стороне ВН трансформаторов =100 МВА, =90 МВА, =72 МВА, линий длиной 55, 70, 90 км. Соs φ=0,8. Напряжение в ЦП 240 кВ.

Пример 19. Мощности нагрузок на стороне ВН трансформаторов =16 МВА, =24 МВА, =19 МВА, линий длиной 14, 21, 22 км. Соs φ=0,94. Напряжение в ЦП 120 кВ.

Пример 20. Мощности нагрузок на стороне ВН трансформаторов =360 МВА, =315 МВА, =420 МВА, линий длиной 235, 155, 200 км. Соs φ=0,91. Напряжение в ЦП 537 кВ.

Пример 21. Мощности нагрузок на стороне ВН трансформаторов =105 МВА, =135 МВА, =215 МВА, линий длиной 90, 88, 75 км. Соs φ=0,98. Напряжение в ЦП 348 кВ.