метод стрельбы для краевой задачи оду. Тестова_задача. 4 розвязання крайової задачі методом стрільби граничні умови
 Скачать 16.69 Kb. Скачать 16.69 Kb.
|
|
4 РОЗВ’ЯЗАННЯ КРАЙОВОЇ ЗАДАЧІ МЕТОДОМ СТРІЛЬБИ 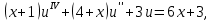 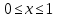 Граничні умови: 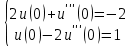 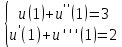 Вводимо нові змінні 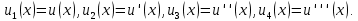 Зводимо дану крайову задачу до крайової задачі для системи диференційних рівнянь 4-го порядку 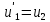 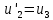 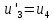 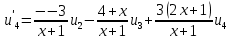 Створюємо процедуру знаходження розв’язку системи, записуємо систему у векторному вигляді 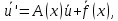 (4.1) (4.1)де 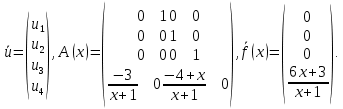 Граничні умови в нових змінних 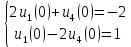 (4.2) (4.2)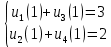 (4.3) (4.3)З умови (4.2) маємо 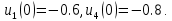 Алгоритм метода стрільби: Розв’язується задача Коші 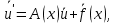 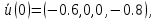 розв’язок позначаємо 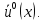 Розв’язуються дві задачі Коші для системи диференційних рівнянь 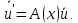 Вектор-функція 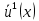 – розв’язок, що задовільняє початковим умовам – розв’язок, що задовільняє початковим умовам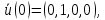 а 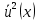 задовільняє початковим умовам задовільняє початковим умовам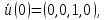 Будуємо вектор-функцію 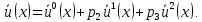 В силу лінійності задачі 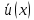 задовільняє системі диференціальних рівнянь (4.1). В точці задовільняє системі диференціальних рівнянь (4.1). В точці 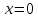 маємо маємо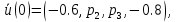 тобто 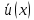 задовільняє крайовим умовам (4.2) також. задовільняє крайовим умовам (4.2) також.Обираємо значення 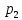 і і 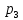 такі, щоб функція такі, щоб функція 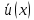 задовільняла крайовим умовам (4.3), тобто задовільняла крайовим умовам (4.3), тобто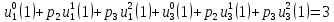 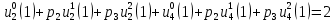 Параметри 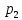 і і 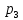 повинні бути розв’язком СЛАР повинні бути розв’язком СЛАР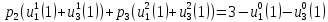 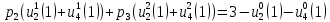 Для розрахунку значень коефіцієнтів і правих частин СЛАР потрібно розв’язати три задачі Коші. Після розрахунку 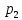 і і 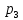 знаходимо розв’язання знаходимо розв’язання 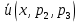 задачі Коші задачі Коші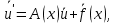 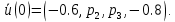 |
