46. Спектр прямоугольного лчмсигнала
 Скачать 430.03 Kb.
|
|
46. Спектр прямоугольного ЛЧМ-сигнала. Радиоимпульсом с линейной частотной модуляцией, или ЛЧМ-импульсом, называется сигнал, представляемый следующей математической моделью: 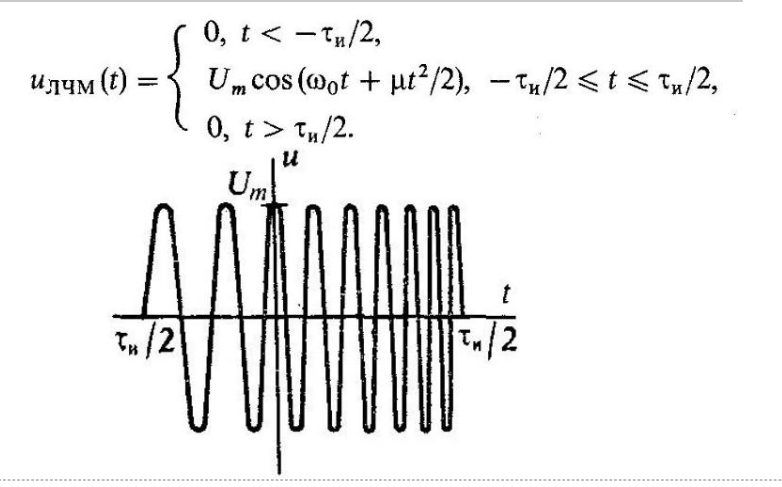 Замечательное свойство ЛЧМ-сигналов, определяющее их практическую значимость, состоит в следующем. Предположим, что имеется некоторое физическое устройство, осуществляющее задержку сигналов, подаваемых на его вход. Если время задержки зависит от частоты сигнала, причем с ростом частоты это время уменьшается, то при определенных условиях, подавая на вход такого устройства ЛЧМ-импульс большой длительности, можно добиться существенного «сжатия» его во времени. Этот эффект обусловлен тем, что на выходе устройства задержки одновременно будут появляться составляющие как более низкочастотные, относящиеся к началу импульса, так и более высокочастотные, наблюдаемые в его конце.  47. Матрицы, виды матриц Матрицами называются массивы элементов, представленные в виде прямоугольных таблиц, для которых определены правила математических действий. Элементами матрицы могут являться числа, алгебраические символы или математические функции. Матрица обозначается одной из заглавных букв латинского алфавита, а набор ее элементов помещается в круглые скобки:
Представленная формулой (1) матрица A имеет m строк и n столбцов и называется m×n матрицей (“эм на эн матрицей”) или матрицей размера m×n. Строки матрицы нумеруются сверху вниз, а столбцы – слева направо ВИДЫ МАТРИЦ Если в матрице число строк равно числу столбцов, то матрица называется квадратной, причём число ее строк или столбцов называется порядком матрицы. В приведённых выше примерах квадратными являются вторая матрица – её порядок равен 3, и четвёртая матрица – её порядок 1. Матрица, в которой число строк не равно числу столбцов, называется прямоугольной. В примерах это первая матрица и третья. Различаются также матрицы, имеющие только одну строку или один столбец. Матрица, у которой всего одна строка  , называется матрицей – строкой (или строковой), а матрица, у которой всего один столбец, матрицей – столбцом.Матрица, все элементы которой равны нулю, называется нулевойи обозначается (0), или просто 0. Например,  .Главной диагональю квадратной матрицы назовём диагональ, идущую из левого верхнего в правый нижний угол.  Квадратная матрица, у которой все элементы, лежащие ниже главной диагонали, равны нулю, называется треугольной матрицей. 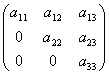 .Квадратная матрица, у которой все элементы, кроме, быть может, стоящих на главной диагонали, равны нулю, называется диагональной матрицей. Например, 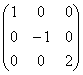 или  .48. Операции над матрицами и их свойства (сложение, умножение на число, умножение, транспонирование) Сложение и вычитание матриц. Суммой A+B матриц Am×n=(aij) и Bm×n=(bij) называется матрица Cm×n=(cij), где cij=aij+bij для всех i=¯¯¯¯¯¯¯¯¯1,m и j=¯¯¯¯¯¯¯¯1,n. Аналогичное определение вводят и для разности матриц: Разностью A−B матриц Am×n=(aij) и Bm×n=(bij) называется матрица Cm×n=(cij), где cij=aij−bij для всех i=¯¯¯¯¯¯¯¯¯1,m и j=¯¯¯¯¯¯¯¯1,n. Умножение матрицы на число. Произведением матрицы Am×n=(aij) на число α называется матрица Bm×n=(bij), где bij=α⋅aij для всех i=¯¯¯¯¯¯¯¯¯1,m и j=¯¯¯¯¯¯¯¯1,n. Произведение двух матриц. Определение этой операции громоздко и, на первый взгляд, непонятно. Поэтому сначала укажу общее определение, а потом подробно разберем, что оно означает и как с ним работать. Произведением матрицы Am×n=(aij) на матрицу Bn×k=(bij) называется матрица Cm×k=(cij), для которой каждый элемент cij равен сумме произведений соответствующих элементов i-й строки матрицы A на элементы j-го столбца матрицы B:cij=n∑p=1aipbpj,i=¯¯¯¯¯¯¯¯¯1,m,j=¯¯¯¯¯¯¯¯1,n. Транспонированная матрица. Транспонированной по отношению к матрице Am×n=(aij) называется матрица ATn×m=(aTij), для элементов которой aTij=aji. 49. Определители второго порядка Определителем второго порядка, соответствующим квадратной матрице второго порядка, называется число, обозначаемое  или  , равное .Правило Определитель второго порядка равен произведению элементов, стоящих на главной диагонали, минус произведение элементов на побочной диагонали. Пример  .50. Определители третьего порядка. Правило треугольников Теперь рассмотрим матрицу третьего порядка Определителем этой матрицы называется число, равное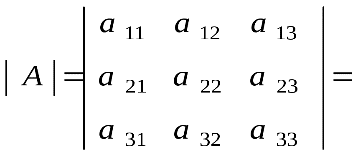 (3) Из выражения (3) следует, что каждый член определителя прежде всего представляет собой произведение трех его элементов, взятых по одному из каждой строки и каждого столбца: со знаком плюс - три члена, состоящие из элементов главной диагонали и из элементов, расположенных в вершинах равнобедренных треугольников с основаниями, параллельными главной диагонали; со знаком минус - три члена, расположенных аналогичным образом относительно побочной диагонали. Схема вычисления определителя третьего порядка изображена на следующих рисунках: 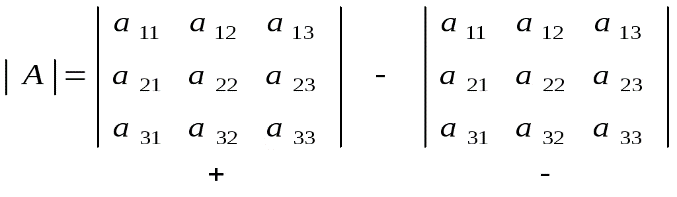 .ПРИМЕР. Вычислить определитель матрицы 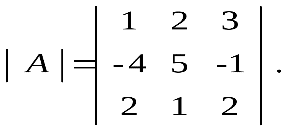  det A= =1·5·2 +3·1·(-4)+2·(-1) ·2 - 2·5·3 - 1·(-1) ·1 - 2· (-4) ·2= -13. Указанное правило вычисления определителя третьего порядка называется правилом треугольников. Наряду с правилом треугольников для вычисления определителей третьего порядка существует правило Саросса . Суть этого правила состоит в том, что справа к исходному определителю добавляются первый и второй столбцы этого определителя, то есть:   . |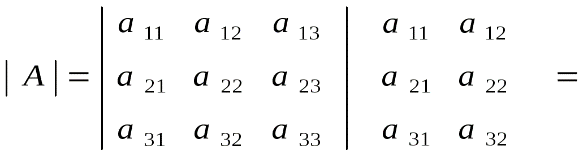
