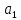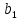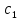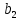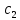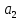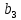лабораторная работа базы данных. Лаб.3 Нормальные формы. 5. Нормализация реляционной модели Функциональные зависимости
 Скачать 146.22 Kb. Скачать 146.22 Kb.
|
|
Поставки товаров Цена товара
Рис.12. Отношения «Поставки товаров» и «Цена товара» 5.3.3. Третья нормальная форма (3НФ) Третья нормальная форма (3НФ) основана на понятии транзитивной функциональной зависимости. Если для атрибутов A, B и C некоторого отношения существуют зависимости вида A  B и B B и B C, то говорят, что атрибут C транзитивно зависит от атрибута A через атрибут B (при этом A функционально не зависит ни от B, ни от C). C, то говорят, что атрибут C транзитивно зависит от атрибута A через атрибут B (при этом A функционально не зависит ни от B, ни от C).Отношение находится в 3НФ, если оно находится во 2НФ и каждый неключевой атрибут нетранзитивно зависит от первичного ключа. Рассмотрим пример приведения отношения «Хранение товаров» (Табл. 7) к 3НФ.
Табл.7. Отношение «Хранение товаров» Известно, что каждая фирма может хранить товары только на одном складе, но на одном и том же складе могут храниться товары, принадлежащие нескольким фирмам. Естественно, каждый склад имеет определенный объем (м3). Семантические ограничения описанного примера можно отразить при помощи функциональных зависимостей. Представим их диаграммой функциональных зависимостей, приведенной на Рис. 13.    Фирма Склад  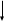  Объем Рис.13. Диаграмма функциональных зависимостей отношения «Хранение товаров» Атрибут «Фирма» является первичным ключом отношения «Хранение товаров». В данном отношении имеется транзитивная зависимость атрибута «Объем» от атрибута «Склад». В связи с этим имеют место аномалии, выявляемые при выполнении операций манипулирования данными: добавления – при добавлении данных о хранении некоторой фирмой товаров на складе требуется также указать фиксированный объем данного склада; обновления – если меняется объем некоторого склада (например, в результате реконструкции), необходимо просмотреть все кортежи отношения, поскольку на одном и том же складе могут храниться товары многих фирм; удаления – в случае, когда некоторая фирма перестала хранить товары на складе, вместе с удалением соответствующего кортежа можно потерять информацию об объеме склада, если на данном складе хранились товары только этой фирмы. Причиной аномалий в отношении «Хранение товаров» является транзитивная зависимость атрибута «Объем» от не ключевого атрибута «Склад». Чтобы привести отношение «Хранение товаров» к 3НФ необходима декомпозиция на два отношения, приведенные на Рис 14. Функциональные зависимости, описанные диаграммой (Рис. 13), очевидно, сохранены. Т.е. декомпозиция выполнена без потерь. Каждое полученное отношение находится в 3НФ, поскольку в каждом отношении имеется только два атрибута, один из которых – первичный ключ. Склады Объемы складов
Рис.14. Отношения «Склады» и «Объемы складов» 5.3.4. Нормальная форма Бойса-Кодда (НФБК) Нормальная форма Бойса-Кодда (НФБК) учитывает функциональные зависимости, в которых участвуют все потенциальные ключи отношения, а не только его первичный ключ. Для отношения с единственным потенциальным ключом его 3НФ и НФБК являются эквивалентными. Отношение находится в НФБК тогда и только тогда, когда каждый его детерминант является потенциальным ключом. Нарушения требований НФБК происходят крайне редко, поскольку это возможно в следующих случаях: имеются два или более составных потенциальных ключа; эти потенциальные ключи перекрываются, т.е. ими совместно используется, по крайней мере, один общий атрибут. Рассмотрим пример приведения отношения «Проекты» (Табл. 8) к НФБК.
Табл.8. Отношение «Проекты» Известно, что в проекте используется несколько деталей, но каждая деталь проекта при этом поставляется только одним поставщиком. Каждый поставщик обслуживает единственный проект, но проекты могут обеспечиваться несколькими поставщиками (разных деталей). Семантические ограничения отношения можно отразить при помощи функциональных зависимостей. Представим их диаграммой функциональных зависимостей, приведенной на Рис. 15.    № детали  № поставщика   Наименование проекта  Рис.15. Диаграмма функциональных зависимостей отношения «Проекты» В качестве первичного ключа отношения «Проекты» принята комбинация атрибутов «Наименование проекта», «№ детали». Данное отношение находится в 1НФ, 2НФ, 3НФ и не находится в НФБК. В связи с этим имеют место аномалии, выявляемые при выполнении операций манипулирования данными, например аномалии: добавления – при добавлении данных о некотором поставщике необходимо создавать фиктивный проект, а также деталь для этого поставщика изменения – при изменения наименования проекта в некотором кортеже, также необходимо просмотреть все отношение и поменять наименование проекта для всех используемых деталей. удаления – при удалении информация о некотором поставщике, удаляется также информация о деталях, которые он поставлял. Причиной аномалий в отношении «Проекты» является то, что не все его детерминанты являются потенциальными ключами (это относится к атрибуту «№ поставщика». Для приведения отношения «Проекты» к НФБК необходима декомпозиция на два отношения, приведенные на Рис 16. Функциональные зависимости, описанные диаграммой (Рис. 15), очевидно, сохранены. Т.е. декомпозиция выполнена без потерь. Каждое полученное отношение находится в НФБК, поскольку в каждом отношении имеется только два атрибута, один из которых – первичный ключ. Поставщики-детали Проекты –поставщики
Рис.16. Отношения «Поставщики-детали» и «Проекты-поставщики» 5.3.5. Четвертая нормальная форма (4НФ) Многозначные зависимости (multi-valued dependency) возникают, например, когда необходимо привести к первой нормальной форме отношение, с независимыми многозначными атрибутами. Пусть имеется два таких атрибута Y и Z. Тогда для получения 1НФ необходимо для каждого набора значений остальных атрибутов X повторить эту строку для каждого сочетания атомарного значения Y с каждым атомарным значением Z, что называется выравниванием таблицы. Образуется многозначная зависимость в которой: каждому значению X соответствует набор значений Y; каждому значению X соответствует набор значений Z; значения атрибутов Y и Z не зависят один от другого. Многозначную зависимость принято обозначать X→→Y|Z, хотя можно было бы указать наличие двух существующих одновременно обычных функциональных зависимостей X→Y и X→Z. Иногда обозначают многозначную зависимость X→→Y или X→→Z. Определение 1 MV-зависимость X→→Y называется тривиальной если 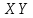 , либо , либо 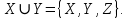 Определение 2: Пусть r – отношение со схемой R(S), а X,Y,Z - непересекающиеся множества его атрибутов, такие, что 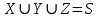 . Атрибуты Y и Z многозначно зависят от X (обозначение X→→Y|Z) если из того, что в отношении r содержатся кортежи r1 = (x, y, z1) и r2 = (x, y1, z) следует, что в отношении r содержится также кортеж r3 = (x, y, z). . Атрибуты Y и Z многозначно зависят от X (обозначение X→→Y|Z) если из того, что в отношении r содержатся кортежи r1 = (x, y, z1) и r2 = (x, y1, z) следует, что в отношении r содержится также кортеж r3 = (x, y, z).Замечание 1: По симметрии определения в r содержится и кортеж r4 = (x, y1, z1). Атрибуты Y и Z как бы симметричны по отношению к X. Замечание 2: При наличии MV-зависимости кортежи обязаны вставляться и удаляться одновременно целыми наборами. Определение 3. Переменная отношения R находится в четвёртой нормальной форме, если она находится в НФБК и все нетривиальные многозначные зависимости фактически являются функциональными зависимостями от её потенциальных ключей. Эквивалентная формулировка определения: Переменная отношения R находится в четвёртой нормальной форме тогда и только тогда, когда в случае существования подмножеств A и B атрибутов этой переменной отношения R, для которых выполняется нетривиальная многозначная зависимость A →→ B, все атрибуты переменной отношения R также функционально зависят от А. Пример: Предположим, что рестораны производят разные виды пиццы, а службы доставки ресторанов работают только в определенных районах города. Составной первичный ключ соответствующей переменной отношения включает три атрибута: {Ресторан, Вид пиццы, Район доставки}. Такая переменная отношения не соответствует 4НФ, так как существует следующая многозначная зависимость: {Ресторан} →→ {Вид пиццы} {Ресторан} →→ {Район доставки} То есть, например, при добавлении нового вида пиццы придется внести по одному новому кортежу для каждого района доставки. Возможна логическая аномалия, при которой определенному виду пиццы будут соответствовать лишь некоторые районы доставки из обслуживаемых рестораном районов. Для предотвращения аномалии нужно декомпозировать отношение, разместив независимые факты в разных отношениях. В данном примере следует выполнить декомпозицию на {Ресторан, Вид пиццы} и {Ресторан, Район доставки}. Однако, если к исходной переменной отношения добавить атрибут, функционально зависящий от потенциального ключа, например цену с учётом стоимости доставки ({Ресторан, Вид пиццы, Район доставки} → Цена), то полученное отношение будет находиться в 4НФ и его уже нельзя подвергнуть декомпозиции без потерь (смотри ниже). Указанные выше многозначные зависимости в данном случае называются внедрёнными зависимостями. 5.3.6. Пятая нормальная форма (5НФ) Декомпозиция без потерь Декомпозицией отношения 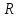 называется замена называется замена 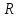 на совокупность отношений на совокупность отношений 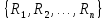 такую, что каждое из них есть проекция такую, что каждое из них есть проекция 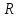 , и каждый атрибут R входит хотя бы в одну из проекций декомпозиции. , и каждый атрибут R входит хотя бы в одну из проекций декомпозиции.Например, для отношения 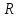 с атрибутами с атрибутами 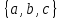 существуют следующие основные варианты декомпозиции: существуют следующие основные варианты декомпозиции: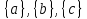 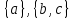 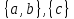 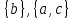 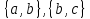 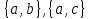 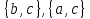 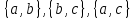 Рассмотрим теперь отношение 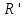 , которое получается в результате операции естественного соединения, применённой к отношениям, полученным в результате декомпозиции , которое получается в результате операции естественного соединения, применённой к отношениям, полученным в результате декомпозиции 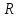 . .Декомпозиция называется декомпозицией без потерь, если 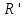 в точности совпадает с в точности совпадает с 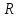 . .Неформально говоря, при декомпозиции без потерь отношение «разделяется» на отношения-проекции таким образом, что из полученных проекций возможна «сборка» исходного отношения с помощью операции естественного соединения. Далеко не всякая декомпозиция является декомпозицией без потерь. Проиллюстрируем это на примере отношения 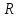 с атрибутами с атрибутами 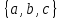 , приведённом выше. Пусть отношение , приведённом выше. Пусть отношение 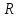 имеет вид: имеет вид: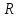
Декомпозиция 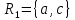 , , 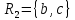 имеет вид: имеет вид: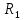 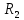
Результат операции соединения этих отношений: 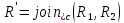
Очевидно, что 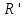 не совпадает с не совпадает с 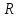 , а значит такая декомпозиция не является декомпозицией без потерь. Рассмотрим теперь декомпозицию , а значит такая декомпозиция не является декомпозицией без потерь. Рассмотрим теперь декомпозицию 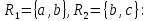 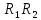
Такая декомпозиция является декомпозицией без потерь, в чём читатель может убедиться самостоятельно. В некоторых случаях отношение вовсе невозможно декомпозировать без потерь. Существуют также примеры отношений, для которых нельзя выполнить декомпозицию без потерь на две проекции, но которые можно подвергнуть декомпозиции без потерь на три или большее количество проекций. Зависимость соединения. Пусть R — переменная отношения, а A, B, …, Z — некоторые подмножества множества её атрибутов. Если декомпозиция любого допустимого значения R на отношения, состоящие из множеств атрибутов A, B, …, Z, является декомпозицией без потерь, говорят, что переменная отношения R удовлетворяет зависимости соединения *{А, В, . . . , Z}. Иными словами, переменная отношения R удовлетворяет зависимости соединения *{А, В, . . . , Z} тогда и только тогда, когда любое допустимое значение переменной отношения R эквивалентно соединению её проекций по подмножествам A, B, …, Z множества атрибутов. Подобно тому, как функциональная зависимость есть частный случай многозначной зависимости, многозначная зависимость является частным случаем зависимости соединения. Зависимость соединения является предельным обобщением понятий многозначной и функциональной зависимости, то есть это наиболее общая форма зависимости между атрибутами отношения. Важно понимать, что зависимость соединения определяется не для конкретного значения переменной отношения в тот или иной момент времени, а по всем возможным значениям. Поэтому понятие зависимости соединения определено не для отношения (конкретного значения), а для переменной отношения. Зависимость соединения определяется не механически по текущим значениям, а следует из внешнего знания о природе и закономерностях данных, которые могут находиться в переменной отношения. То же самое относится к многозначной и функциональной зависимостям. Зависимость соединения *{A, B,…, Z} является тривиальной тогда и только тогда, когда по крайней мере одно из подмножеств A, B, …, Z является множеством всех атрибутов отношения (включает все атрибуты). В противном случае зависимость соединения является нетривиальной. Формулировка определения Отношение находится в пятой нормальной форме (иначе — в проекционно-соединительной нормальной форме) тогда и только тогда, когда каждая нетривиальная зависимость соединения в нём определяется потенциальным ключом (ключами) этого отношения. Зависимость соединения *{A, B,…, Z} определяется потенциальным ключом (ключами) тогда и только тогда, когда каждое из подмножеств A, B, …, Z множества атрибутов является суперключом отношения. Условие «каждое из подмножеств A, B,…, Z множества атрибутов является суперключом отношения» можно эквивалентно сформулировать так: «каждое из подмножеств A, B, …, Z множества атрибутов включает некоторый потенциальный ключ отношения». Свойства 5НФ Любое отношение в 5НФ автоматически находится также в 4НФ и, следовательно, во всех других нормальных формах. 5НФ является окончательной нормальной формой (по крайней мере в контексте операций проекции и соединения). Рональд Фейгин в 1979 г. показал, что любая переменная отношения может быть подвергнута декомпозиции без потерь на эквивалентный набор переменных отношения в 5НФ, то есть 5НФ всегда достижима. Однако Кристофер Дейт отмечает, что процедура определения того, что некоторая переменная отношения находится в 4НФ, а не в 5НФ, и, таким образом, существует возможность её дальнейшей выгодной декомпозиции, всё ещё остаётся не вполне ясной. Это связано с тем, что задача определения всех зависимостей соединения для отношения может оказаться очень сложной, а по поводу отношения можно утверждать, что оно находится в 5НФ, только при условии известности всех его потенциальных ключей и всех его зависимостей соединения. Очень редко отношение, находящееся в 4НФ, не соответствует 5НФ. Это те ситуации, в которых реальные правила, ограничивающие допустимые комбинации атрибутов, никак не выражены в структуре отношения (см. пример ниже). В таком случае, если отношение не приведено к 5НФ, бремя обеспечения логической целостности данных отчасти перекладывается на приложение, отвечающее за добавление, удаление и изменения данных. В этом случае существует риск возникновения ошибок. Пятая нормальная форма исключает возникновение таких аномалий. Пример: схема из трёх сущностей со связями многие-ко-многим, а именно -- автомобиль; -- цвет кузова; -- модель. Ассоциативные сущности: модель – цвет, автомобиль – цвет, автомобиль – модель. Добавляем ассоциативную сущность модель – цвет – автомобиль 5.4. Задания по нормализации для аудиторной и самостоятельной работы Задано отношение и множество функциональных зависимостей. Определить ключ, выявить текущую нормальную форму и преобразовать это отношение к 2НФ, 3НФ, НФБК, 4НФ, подтверждая на каждом шаге правильность результата. Задача 1. Задано отношение Рабочий: |