5. Синтез зубчатого механизма Исходные данные для расчета эпициклического механизма Рис. 4

• Название: 5. Синтез зубчатого механизма Исходные данные для расчета эпициклического механизма Рис. 4
• Дата: 21.02.2019
• Размер: 106 Kb.
• Имя файла: 3...2.doc
• Тип: Документы; #68521

2. Схемы механизмов, структура и исходные данные для проектирования
5. Синтез зубчатого механизма

5.1. Исходные данные для расчета эпициклического механизма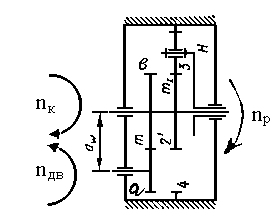



Рис.4 Схема зубчатого механизма

Зубчатый механизм с двухступенчатой планетарной и простой передачей:

• 
  частота вращения электродвигателя: n_дв=1500 об/мин ;
  
• 
  частота вращения коленчатого вала: n₁= n_p=180 об/мин;
  
• 
  модуль зубчатых колес планетарного механизма: m₁= 4 мм;
  
• 
  модуль зубчатых колес Z_а и Z_b: m = 5 мм;
  
• 
  число зубьев колес простой передачи: Z_a= 13; Z_b= 20.
  

5.2. Геометрический синтез планетарного механизма

В практике машиностроения одной из наиболее важных проблем является выбор рациональной схемы и определения чисел зубьев колес планетарного механизма. Выбор той или иной схемы планетарного механизма производят с учетом необходимого передаточного отношения технологических и конструктивных требований, условий геометрического характера. При проектировании эпициклических механизмов с заданным передаточным отношением возникает задача определения чисел зубьев колес, при следующих условиях:

1. 
   Кинематическое условие.
   
2. 
   Условие соосности.
   
3. 
   Условие соседства.
   
4. 
   Условие сборки.
   

1. Кинематическое условие – условие соответствия заданному передаточному отношению. Общее передаточное отношение найдем по формуле:

i_общ= i_ред* i_ав; i_ав= Z_в/ Z_а= 20/3 =1.44;

i_общ= n_дв/ n_р=1500/180 = 9.38;

i_ред= i_общ/ i_ав= 9.38/1.44 =3.84 .

2. Условие соосности – обеспечивает зацепление сателлитов с центральными колесами при расположении осей центральных колес и водила на одной прямой. Подбираем число зубьев планетарного механизма.

Передаточное отношение ab:

i_ab=-Z_b/Z_a=-20/13=-1.44.

Принимаем число сателлитов, равное 3. Передаточное отношение обращённого механизма:

i^H₁₃=1/i^H₃₁=1/(1-i’_3H)=1/(1-3)=-1/2.

Принимаем:

i^H₁₃=-(B*D)/(A*C)=-(1*10)/(5*4)=-1/2,

т.е. A=5, B=1, C=4, D=10.

Проверяем существование решения:

B/(A+B)=1/(5+1)=0,17<=sin(π/3)=0,87>=C/(D-C)=4/(10-4)=0,67=>

решение существует.

Вычисляем величины:

P₁=3*(D-C)*A*C=3*6*5*4=360; P₂=3*(D-C)*B*C=3*6*1*4=72;

P₃=3*(A+B)*C²=3*6*4²=288; P₄=3*(A+B)*C*D=3*6*4*10=720;

P₅=(1+3n)*(D-C)*(A*C+B*D)=(1+3n)*6*(5*4+1*10)=(1+3n)*180,

где n-целое число.

Наибольший общий делитель этих чисел: λ=36 при любом n.

Определяем числа зубьев колёс в виде:

Z₁=P₁/λ*t=10t; Z₂=P₂/λ*t=2t; Z₂’=P₃/λ*t=8t; Z₃=P₄/λ*t=20t;

Выбираем t из условия отсутствия зубьев:

Z₁>=17, Z₂>=17, Z₂’>=20, Z₃>=85=>t=9.

Отсюда: Z₁=90, Z₂=18, Z₂’=72, Z₃=180.

3. Условие соседства – обеспечивает совместное размещение нескольких сателлитов по общей окружности так, чтобы они не задевали друг друга своими зубьями, учитывается при числе сателлитов больше двух, при этом увеличение числа сателлитов уменьшает нагрузку на зубья:

(Z₂+ 2)/( Z₁+ Z₂)=(18+2)/(90+18)=0,185<=

sin(/3)=0,87

>=(Z₂’+ 2)/( Z₁+ Z₂) (72+2)/(90+18)= 0,69.

Условие соседства выполняется и полученное решение по габаритам является наиболее оптимальным.

Определяем диаметры зубчатых колес:

d₁= m₁* Z₁=4*90 = 180 мм;

d₂= m₁* Z₂= 4*18 = 36 мм;

d₂’= m₁* Z₂’= 4*72 = 144 мм;

d₃= m₁* Z₃= 4*180 = 360 мм.

Для построения картины скоростей выбираем масштаб: _s=0,015 .

5.3. Графический метод кинематического анализа механизма

Составляем в масштабе картину скоростей механизма по найденным диаметрам, отмечаем на ней характерные точки (центры колес) - точки и полюсы их зацепления. Определяю линейную скорость точки А:

V_A=r₁*₁;

V_A=(d₃/2)*(n_дв/30)=(3,14*0,18*1500)/60= 14.13 м/с.

Масштаб построений _V=V_A/А=14.13/100=0,1413 . Длина отрезка скорости V_A равна 100 мм.

Приступаем к построению плана частот вращения. Ставим полюс Р и вертикально ставим точку S. Отрезок РS=h=50мм. Через точку S, перпендикулярно к отрезку РS, проводим прямую -. Через точку Р провожу лучи, параллельные тэта-линиям, до пересечения их с прямой -. На этой прямой получаем соответствующие точки.

Масштаб плана частот вращения находим по формуле:

_n=(30_V)/(π_Sh)= 30*0,1413/3,14*0,015*50 = 1.8 .

5.4. Расчет параметров корригированных зубчатых колес

1. 
   Окружной шаг по делительной окружности:
   

P = *m;

P = 3,14*4= 12.56 мм.

2. 
   Угловой шаг:
   

₁= 2/Z_a; ₂= 2/Z_b;

₁= 4*3,14/13 = 1,4; ₂= 4*3,14/20 = 0,6.

3. 
   Радиус делительной окружности:
   

r₁= m Z_a/2; r₂=m Z_b/2;

r₁=4*13/2 =18 мм; r₂= 4*20/2 = 44 мм.

4. 
   Радиус основной окружности (при = 20˚):
   

r_B1= r₁cos; r_B2= r₂cos;

r_B1= 13*cos20 = 8,46 мм; r_B2= 20*cos20= 20.67 мм.

5. Относительное смещение инструментальной рейки при нарезании колес (коэффициент коррекции):

χ₁= (17 Z_a)/17; χ₂=0;

χ₁= (1713)/17 = 0.47 .

6.Толщина зуба по делительной окружности:

S₁= m (/2 2 χ₁ tg); S₂= m(/22 χ₂ tg);

S₁= 4(3,14/22*0,47*tg20) = 7.65 мм; S₂= 4(3,14/22*0*tg20)= 6.28 мм.

7. Межосевое расстояние и угол зацепления:

inv_w=inv20=0,014904+2*(0,47 +0)*tg20/(13+20)= 0,0242 ;

_w= 23;

a_w== = 64.22 мм.

8. Радиус начальной окружности:

r_w1= r₁*cos/cos_w; r_w2= r₂*cos/cos_w;

r_w1= 13*cos20/cos25= 9.33 мм;

r_w2= 20*cos20/cos25= 22.81 мм.

9. Радиус окружностей впадин:

r_f1= 0,5m*(Z_a2,52 χ₁); r_f2= 0,5m*(Z_b2,52 χ₂);

r_f1= 0,5*4*(132,52*0,47) = 14.88 мм;

r_f2= 0,5*4*(202,5+2*0) = 39 мм.

10. Радиус окружности вершин:

r_a1= a_w r_f20,25m; r_a2= a_w r_f10,25m;

r_a1= 64.22390,25*4 = 24.22 мм;

r_a2= 64.2214.880,25*4 = 48.34 мм.

11. Длина активной части линии зацепления:

g=  asin;

g= 64.22*sin25 = 39.25 мм.

12. Коэффициент перекрытия:`

_α= g/*m*cos;

_α= 39.25/3,14*4*cos20= 3.33 .

6. Построение эвольвенты

Построение ведем в масштабе 6:1. Построение профилей производим в следующем порядке:

1. 
   наносим положение центров колес – точки О и О;
   
2. 
   проводим дуги начальных окружностей, соприкасающихся в полюсе зацепления Р;
   
3. 
   строим остальные окружности зубчатых колес: делительные (r, r), основные (r, r), впадин (r, r) и вершин (r, r);
   
4. 
   через полюс зацепления проводим общую касательную к начальным окружностям t-t и линию зацепления n-n, касающуюся основных окружностей в точках А и В;
   
5. 
   строим эвольвенты двух зубчатых колес, соприкасающиеся в полюсе зацепления Р. Отрезок АР делим на четыре равные части. Эти отрезки откладываем по основной окружности первого класса вправо и влево от точки А, получаем точки 0,1,….,8. Через эти точки (кроме 0) проводим касательные к основной окружности. Если на касательной, проведенной через точку 1, отложить ¼ отрезка АР, то получим точку 1. На касательной 2 отложим два отрезка, равных ¼ АР, и получим точку 2. Проведя аналогичные построения на каждой из касательных, получим ряд точек: 1, 2 и т.д. Плавная кривая, проведенная через полученные точки, является эвольвентным профилем правой части зуба первого колеса. Точно таким же способом строится эвольвентный профиль зуба второго колеса (для этого используется отрезок ВР). Вторую половину эвольвенты строим с помощью шаблона. Остальные профили зубьев строим также с помощью шаблона;
   
6. 
   профиль ножки зуба выполняется радиусом 0,4m.
   

7. Список использованной литературы

1. 
   Алехнович Н.В. Теория механизмов и машин. Сборник контрольных работ и курсовых проектов. Минск, 1970г. Высшая школа, 252 с.
   
2. 
   Артоболевский И.И. Теория механизмов и машин. М.Наука,1975г., 640 с.
   
3. 
   Недоводеев В.Я. Кинематическое исследование и синтез планетарных зубчатых механизмов. Методические указания к курсовому проекту по теории механизмов и машин. Ульяновск, 1988г., 23 с.
   
4. 
   Недоводеев В.Я. Теория механизмов и машин. Методические указания и задания к курсовому проекту для студентов машиностроительных специальностей. Ульяновск, 2000г., 28 с.
   
5. 
   Недоводеев В.Я. Структурный, кинематический и силовой анализ плоских рычажных механизмов. Ульяновск, 1990г., 35 с.
   
6. 
   Попов С.А., Тимофеев Г.А. Курсовое проектирование по теории механизмов и машин. М.: Высшая школа, 1999г., 348 с.
   
7. 
   Юдин В.А., Петрокас Л.В. Теория механизмов и машин. М.: Высшая школа, 1977г., 527 с.
   
8. 
   Фролов К.В., Попов С.А., Мусатов А.К. и др. Теория механизмов и машин. Учебник для вузов. Под редакцией Фролова К.В. М.: Высшая школа, 1987г., 496 с.