5 зертханалы жмыс Пні Басару объектілерін моделдеу жне идентификациялау
 Скачать 0.52 Mb. Скачать 0.52 Mb.
|
|
Коммерциялық емес акционерлік қоғам «Ғұмарбек Дәукеев атындағы АЛМАТЫ ЭНЕРГЕТИКА ЖӘНЕ БАЙЛАНЫС УНИВЕРСИТЕТІ» «Автоматтандыру және басқару» кафедрасы №5 зертханалық жұмыс Пәні: «Басқару объектілерін моделдеу және идентификациялау» Мамандығы: 6B07108 – «Автоматтандыру және басқару» Орындаған: Тобы: Нұсқа: 28 Тексерген: аға оқытушы Маркабаева Ж. С. _____________ _____________ «___» ____________ 2023 ж. (бағасы) (қолы) 5 Зертханалық жұмыс №5. Сызықты динамикалық объекттерді параметрлік идентификациялауЖұмыс мақсаты: объектілерді параметрлік идентификациялау әдістерін және сәйкессіздік функционалын минимумдау процедурасын игеру. 5.1 Зертханалық жұмысқа тапсырмаЗертханалық жұмысты жасау барысында студент келесі тапсырмаларды орындау керек: -сызықты динамикалық объектілерді параметрлік идентификациялау әдістерімен танысу [3,4]; -ортақвадратты критерийді минимумдау процедурасын оқу[1,3]; - объектіде тәжірибелерді орындау: объект кірісіне берілген кіріс сигналын беріп, шығыс сигналдың сандық мәндерін тіркеңіз; - қисықтарды қиыстыруCurve Fitting Toolbox пакетін қолданып, шығыс сигналды таңдалынған теңдеулермен жуықтаңыз (аппроксимациялаңыз); - объектініңсызықты динамикалық моделінің құрылымын таңдаңыз; - таңдалынған құрылым үшін сәйкессіздік функционалының түрін жазыңыз; - тәжірибелер нәтижелерін қолданып осы функционалды минимумдау есебін шешіңіз; модель параметрлерін анықтаңыз; -құрастырылған моделдің дәлдігін бағалаңыз. Зертханалық жұмысты орындау тәртібі1 кесте – Кіріс сигналдар мен модельдердің құрылымдық параметрлері
5.4.1 Идентификациялау процедурасын орындауға «өлшеу стендін» құрыңыз: - Work/Objects5 папкасынан Simulink ортасына «объектіні» жүктеңіз (нұсқа бойынша – 5.1 кесте); - кіріс сигнал үшін диаграмманы жинаңыз (нұсқа бойынша), оны объект кірісіне беріңіз; - шығыс сигналдың мәндерін Matlab жұмыс ортасына орнатыңыз; ол үшін сигналды To Workspace блогына беріңіз, осы блок атауына сәйкес айнымалының атын орнатыңыз. To Workspace блогының баптау терезесінде Array опициясын таңдаңыз – сонда сигналдың сандық мәндерінің массивін аламыз. 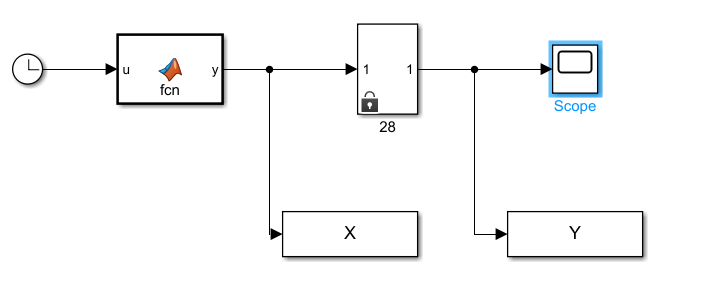 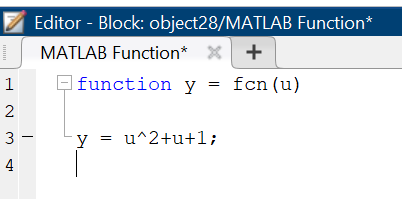 1 сурет – Нұсқа бойынша объект 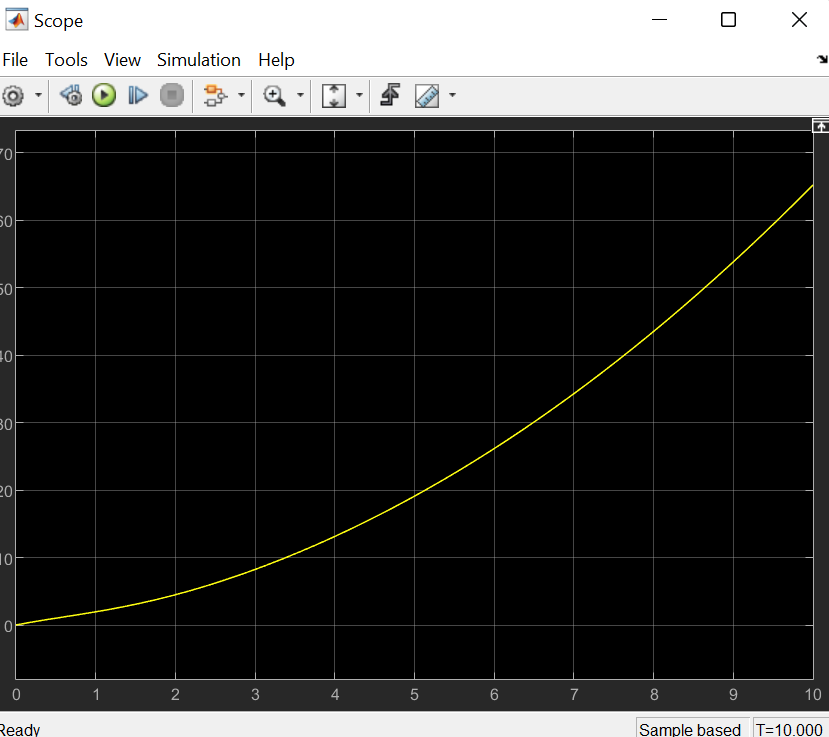 2 сурет – Нұсқа бойынша берілген функцияның өтпелі процессі Бұл №5 зертханалық жұмысты орындау барысында функцияны аппроксимациялауымыз қажет. Ол үшін Matlab программасында Curve Fitting Toolbox ортасында жұмыс жасаймыз. >>cftool командасын терген соң, Curve Fitting Toolbox терезесі ашылады.  3 сурет – cftool командасы Идентфикациялау процедурасын қарастырылып отырған параметрлік әдісімен орындау үшін кіріс және шығыс сигналдарының аналитикалық өрнектері қажет. Шығудағы сигнал мәліметтер массиві ретінде алынды, сондықтан оны аппроксимациялау қажет. Аппроксимациялау есебі Curve Fitting Tool пакеті көмегімен шешіледі. 5.4.2 Curve Fitting Tool пакетін жүктеу үшін бұйрық жолда cfrool теріңіз. Шығыс сигналдың мәндерін пакет терезесіне көшіріңіз; нүктелердің орналасуына қарай аппроксимациялау полиномның түрін таңдаңыз. 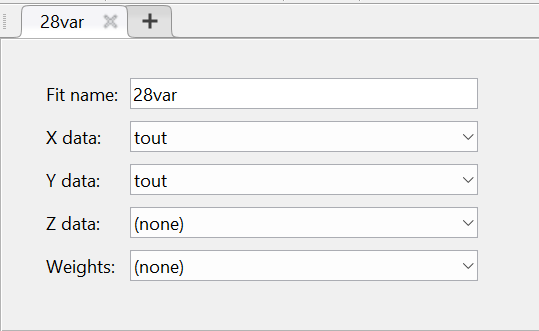 4 cурет – Мәліметтерді орнату X data батырмасын басып X, ал Y data үшін Y деп таңдаймыз. Төменгі жақ терезеде нүктелер жиыны пайда болады (бастапқы мәліметтер). Шығыс сигналдың мәндерін әртүрлі функциялармен жуықтаңыз: әртүрлі ретті полиномдарымен немесе кейбір таңдалынған теңдеулермен. Өз теңдеуіңізді орнату үшін регрессиялар түрлерінің тізімінен Custom equations жолын таңдаңыз. Create Custom Equations терезесі пайда болады. Бұл терезенің екі беті бар. Бірінші Linear Equations бетінде коэффициенттер бойынша сызықты теңдеудің параметрлері орнатылады. Тәулділіктің өзі сызықты емес болуы мүмкін. Екінші General Equations бетінде регрессияның кезкелген сызықты емес теңдеуін орнатуға болады. 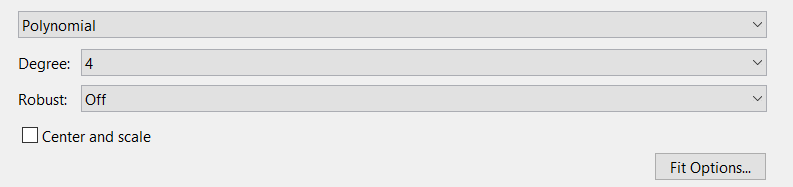 5 сурет – Регрессия түрін таңдау Регрессияны орындау үшін «Type of fit» менюден «Polynomial» типін таңдаймыз. «Number of terms» батырмасын басу арқылы оның ретін таңдаймыз. Біріншіден, оның ретін 4 деп алып, нәтижесін 6-шы суреттен көре аламыз. Солардың коэффициенттерін біз Results терезесінде көруге болады. Осы коэффициенттердің мәндерін алу арқылы, полимном функцияның жуықтау графигін тұрғызамыз. 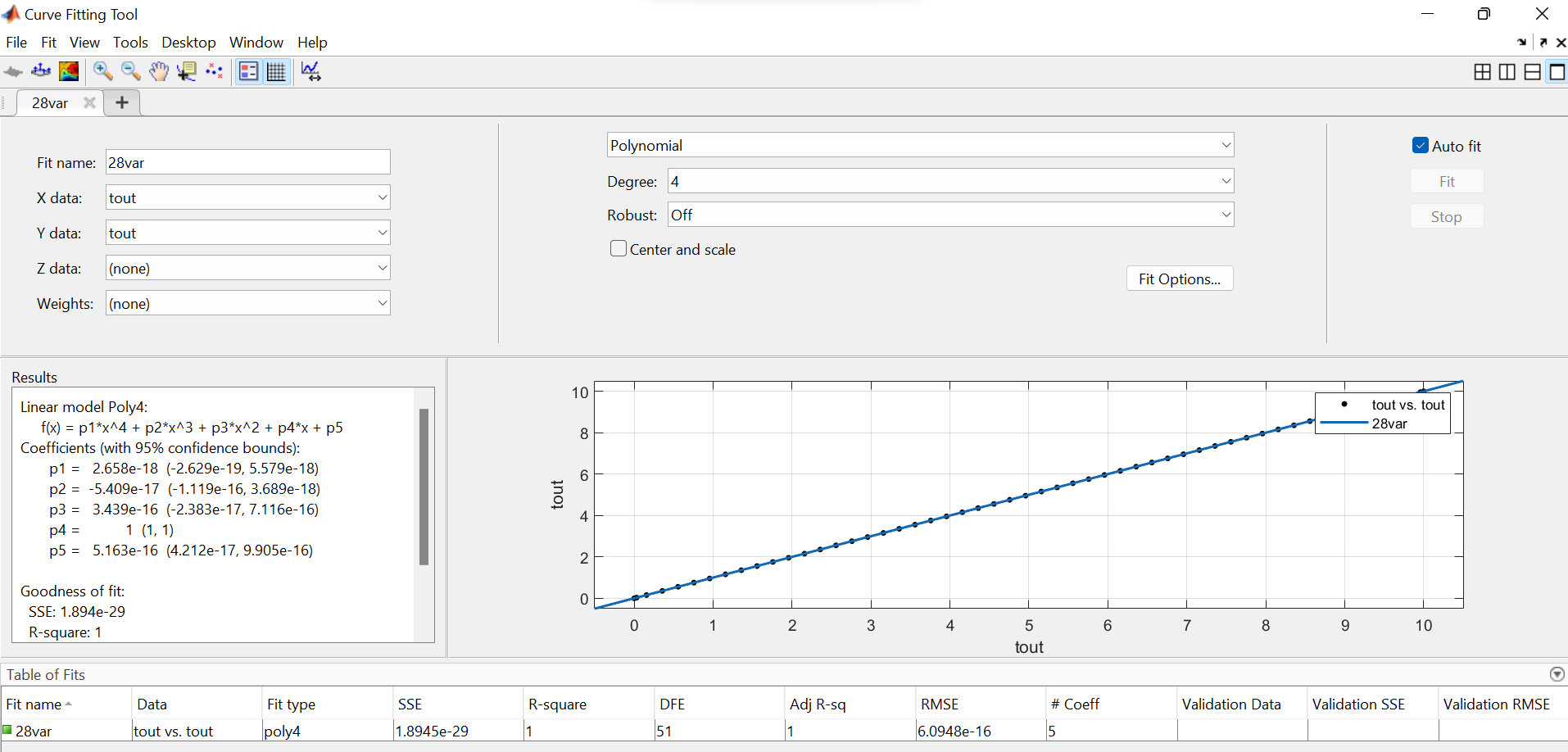 6 сурет – Полиномды жуықтау функциясы Функцияны 4-ретті Полиномды жуықтау функция деп аламыз. Біздің мақсатымыз, бастапқы функцияға жуықтау (аппроксимациялау). Екі график бір-біріне сәйкес келмейінше оның ретін жоғарылата береміз. 5.4.3 Қиыстыруды аяқтап, шығыс сигналды ең тиімді жуықтайтын функцияны таңдаңыз. Осы функцияның өрнегін жазыңыз (есептелген коэффициенттерлер мәндерімен). 5.4.4 Берілген құрылымдық параметрлерін (нұсқа бойынша) қолдана модельдің теңдеуін дифференциалды теңдеу түрінде жазыңыз. Модельдің құрылымдық параметрлері: p=3, l=1. 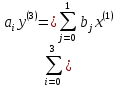 Дифференциалды теңдеу 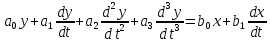 Беріліс функциясын табамыз: 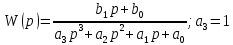 5.4.5 Сәйкессіздік функционалының түрін жазыңыз: кіріс функциясы мен оның туындылары орнына кіріс сигнал мен оның туындыларының өрнектерін қойыңыз; шығыс функциясы мен оның туындылары орнына жуықтау барысында алынған өрнек пен оның сәйкес туындыларын қойыңыз. Сәйкессіздік функционал келесідей құрастырылады: 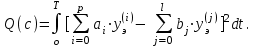 Q функционал невязка деп аталады, ол А операторына тәуелді. Сонымен модель мен объект операторларының невязка дәрежесін (сәйкессіздік дәрежесін) А модель операторынан нақты түрде тәуелді функционалмен көрсетуге болады. Әрине, идентификациялау процесін невязканы минимумдау жолымен өткіземіз, яғни Q функционалын А операторлар бойынша минимумдау есебін шешеміз: Осы функционалды ai мен bj бойынша минимумдаймыз: Минимумдау нәтижесі – с* векторы идентификацияланатын параметрлер мәні болып табылады. Бұл функционалды минимумдағанда, А операторын еркін таңдамаймыз, оларды белгілі операторлар класынан Ω таңдаймыз. Функциясының барлық белгісіз параметрлері бойынша туындыларын нөлге теңестіріп сызықты теңдеулер жүйесін аламыз, осы жүйенің шешімі минимумдау есебінің шешімі болады. 5.4.6 Сәйкессіздік функционалдың барлық айнымалылары бойынша туындыларын нолге теңестіріп, сызықты алгебралық теңдеулер жүйесін алыңыз (осы модельдің параметрлерін анықтауға негізделген жүйе). Сызықты алгебралық теңдеулер жүйесінің коэффициенттері әртүрлі анықталған интегралдар түрінде жазылады. Интегралдар мәндерін есептеуге Matlab жүйенің бұйрық терезесінің мүмкіншіліктерін қолданыңыз. 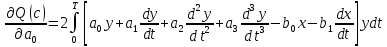 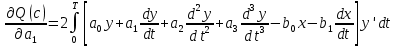 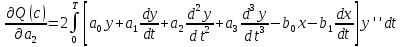 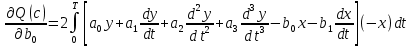 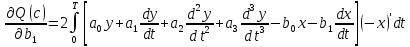 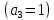 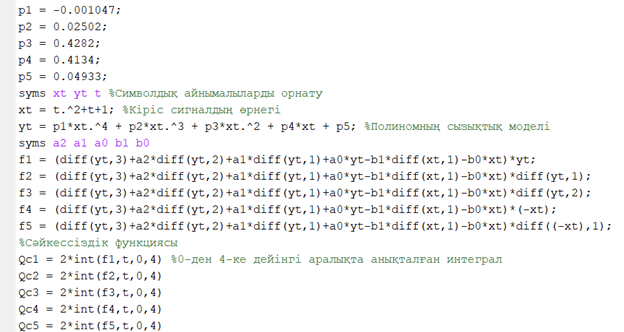 7 Сурет – Матлаб жұмыс терезесіндегі өрнектерді дифференциалдау мен интегралдау бұйрықтар 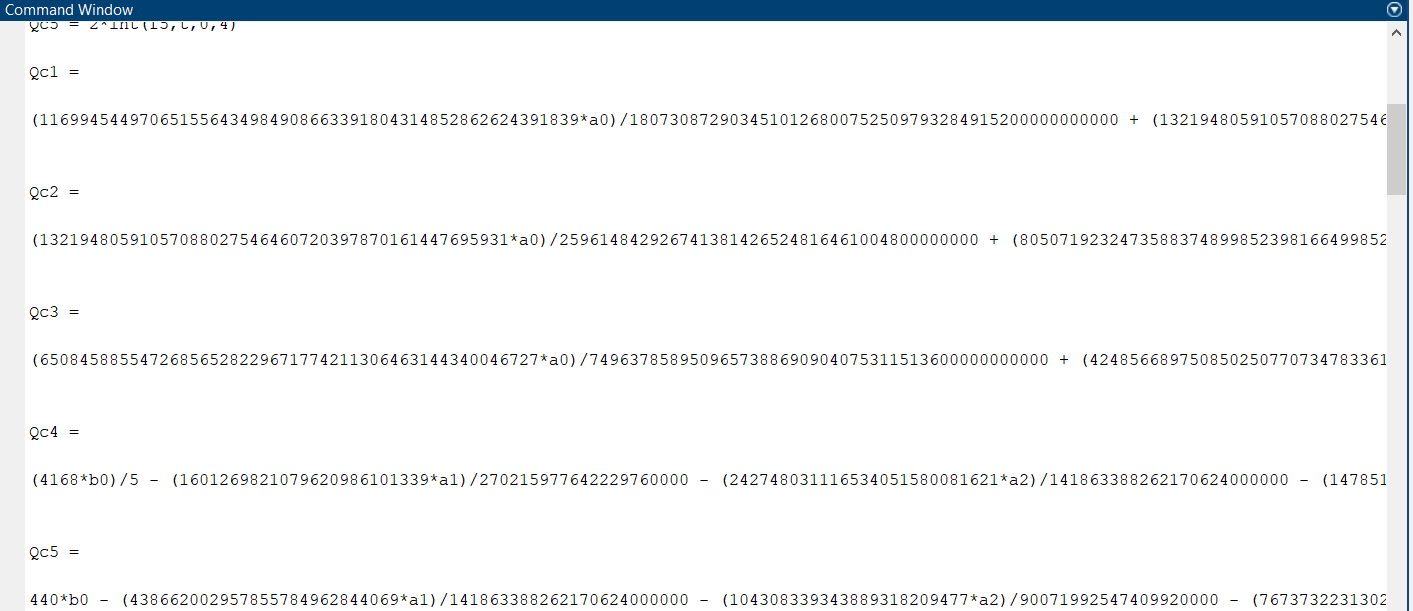 9 cурет – Qc cәйкессіздік функциялары 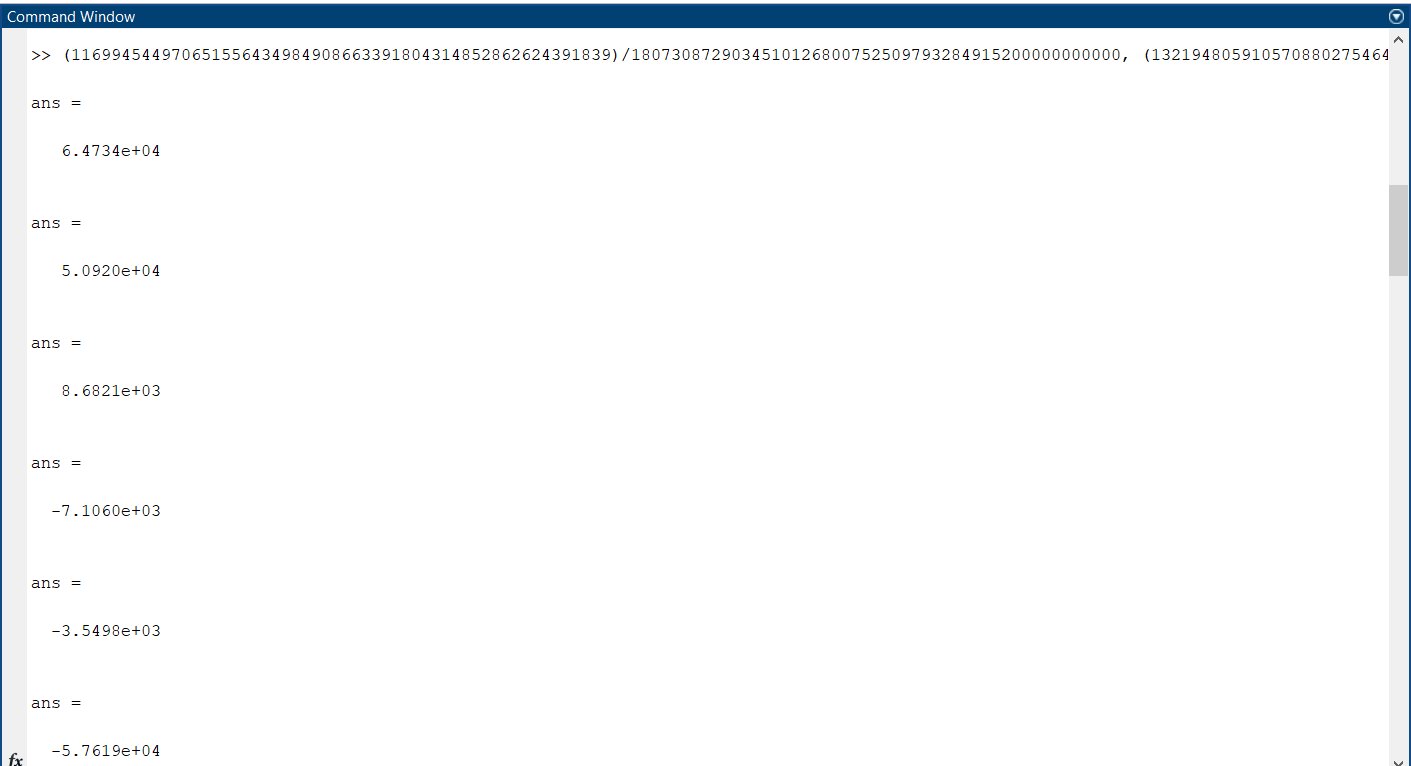 10 cурет – Qc1 коэффициенттері 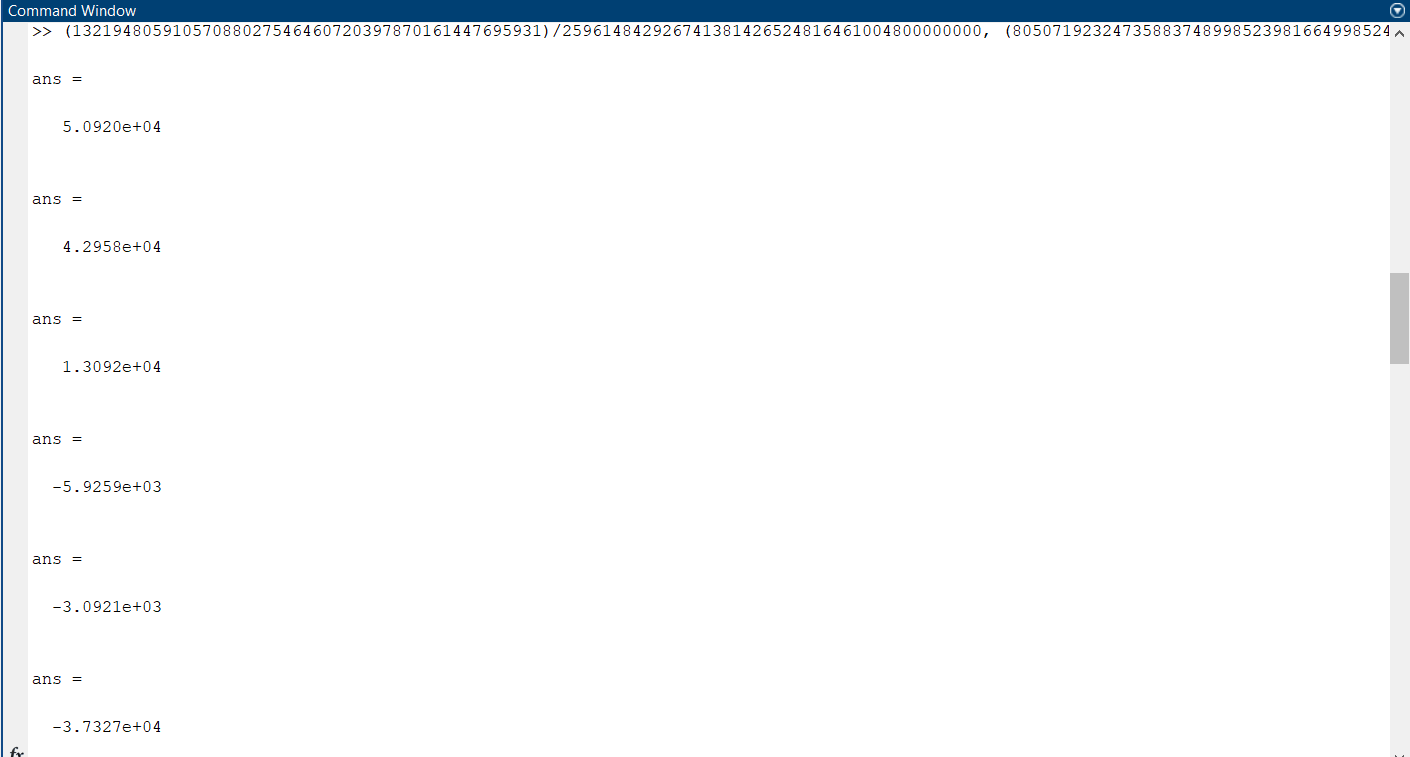 11 cурет – Qc2 коэффициенттері 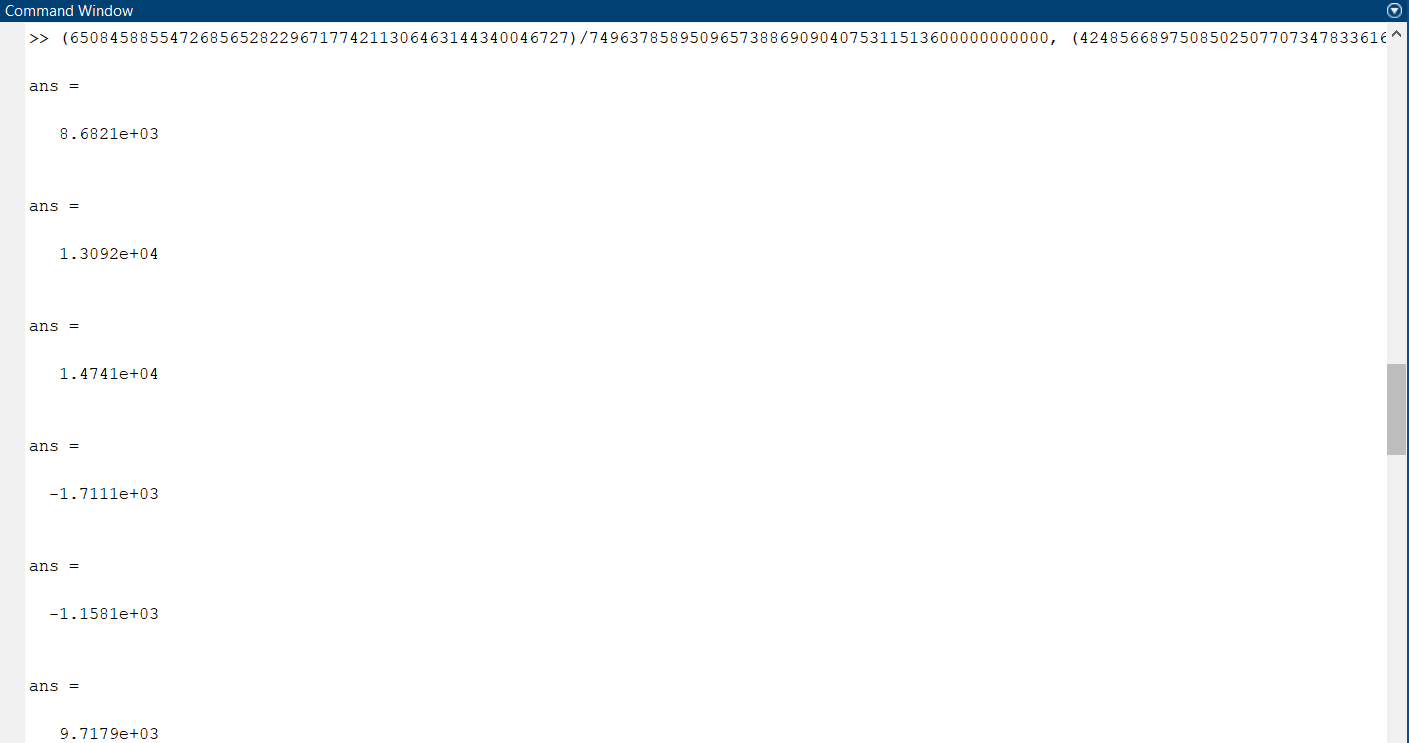 12 cурет – Qc3 коэффициенттері 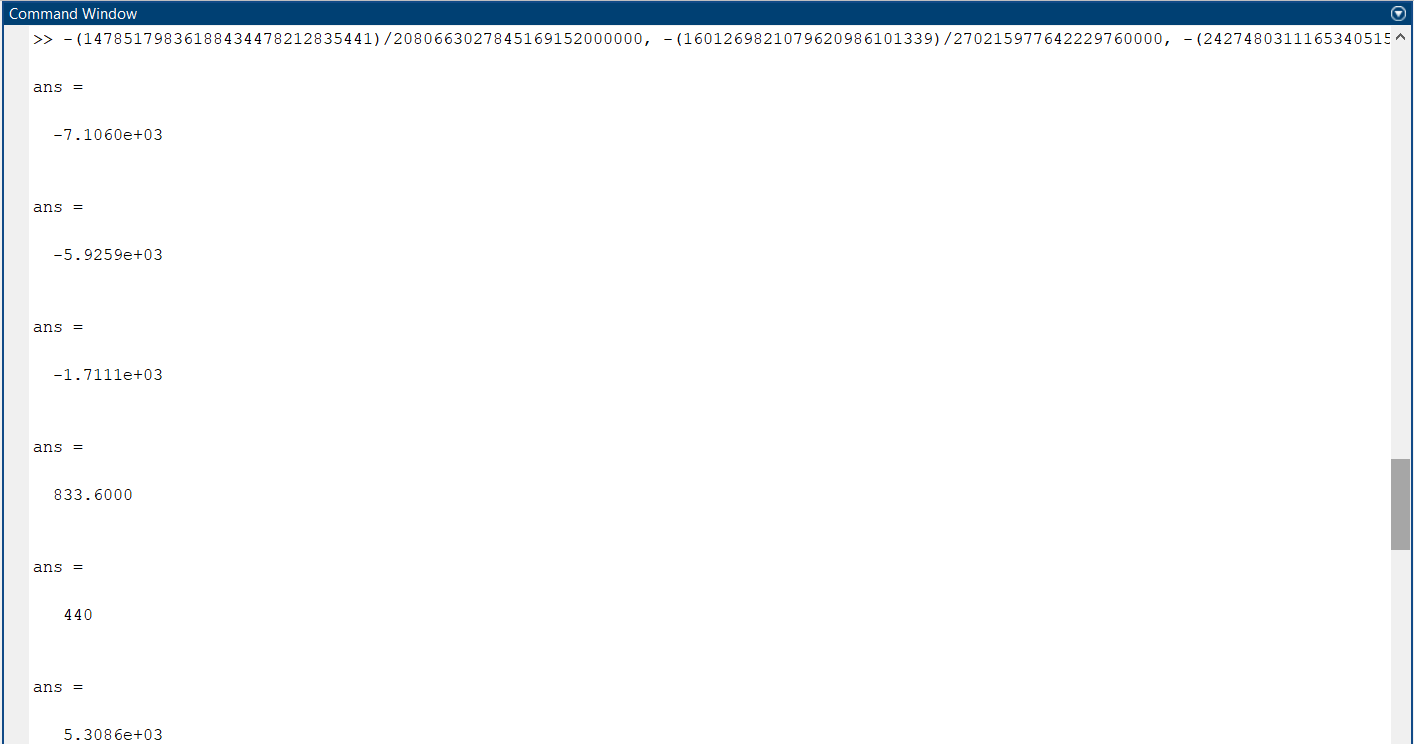 13 cурет – Qc4 коэффициенттері 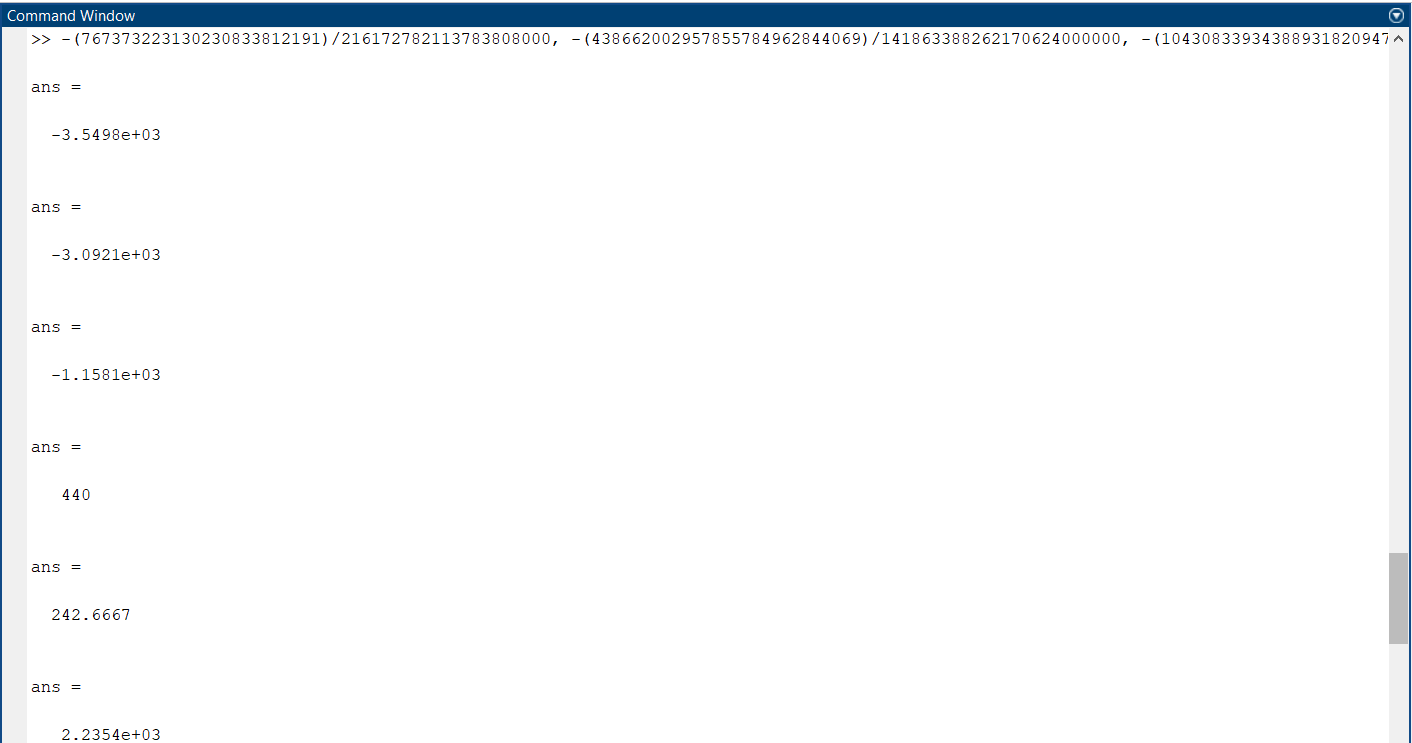 14 cурет – Qc5 коэффициенттері 5.4.7 Біріншіден алынған жүйенің коэффициенттерін есептеп (интегралдар мәндерін), оны сызықты алгебралық теңдеулер жүйесінің стандартты түріне түрлендіріңіз: 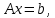 мұндағы А - жүйе матрицасы; b – жүйенің оң жақтағы векторы; x–белгісіздер векторы (моделдің параметрлері). 5.4.8 Осы жүйені Matlab-тың процедурасы көмегімен шешіңіз (бұйрық терезеде); стандартты түрдегі жүйе үшін: 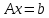 шешім келесідей табылады: 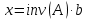 Алдын-ала А (матрица) және b (тік жол векторы) массивтерін Matlab ортаның бұйрық терезесіне енгізу керек, сонымен бірге жүйенің шешім бар болатын det(A) 0 шартын тексеру керек. 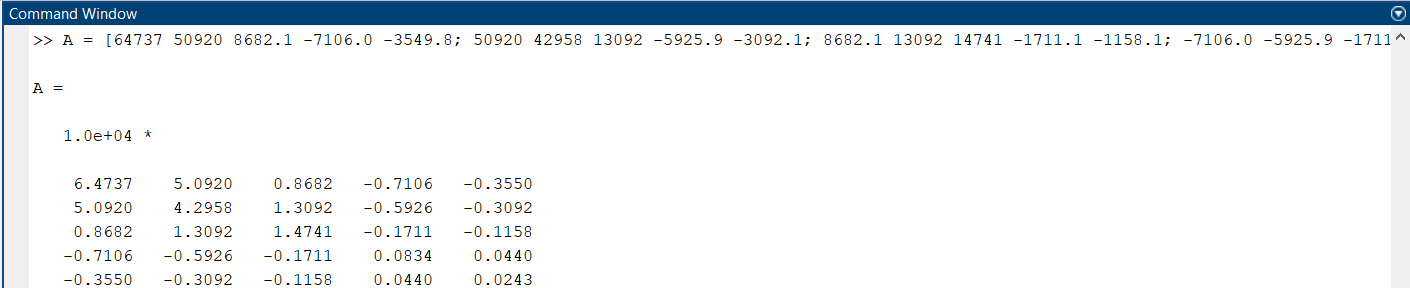 15 сурет – А матрицасы 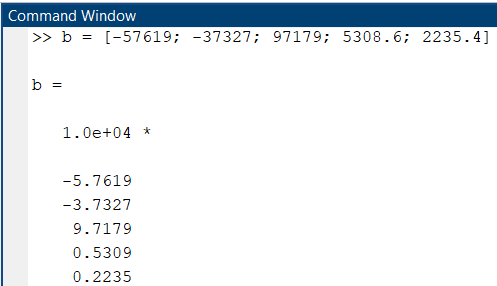 16 сурет – b баған фекторы 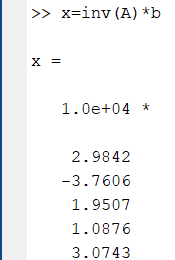 17 сурет – Нәтижесі Алынған мәндер: 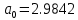 ; ;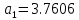 ; ;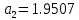 ; ;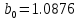 ; ;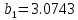 ; ;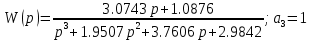 5.4.9 Параметрлердің табылған мәндерін қолданып, динамикалық моделдің ізделінген дифференциалды теңдеуін жазыңыз. Модельді беріліс функция түріне түрлендіріңіз. 5.4.10 5.4.1 тарауында іске асырылған диаграммаға моделдің блогын қосыңыз; оның кірісінеде орнатылған кіріс сигналды беріңіз; объект пен модельдің шығыстарын бір терезеге шығарыңыз (модель Transfer Function блогымен жасалады). 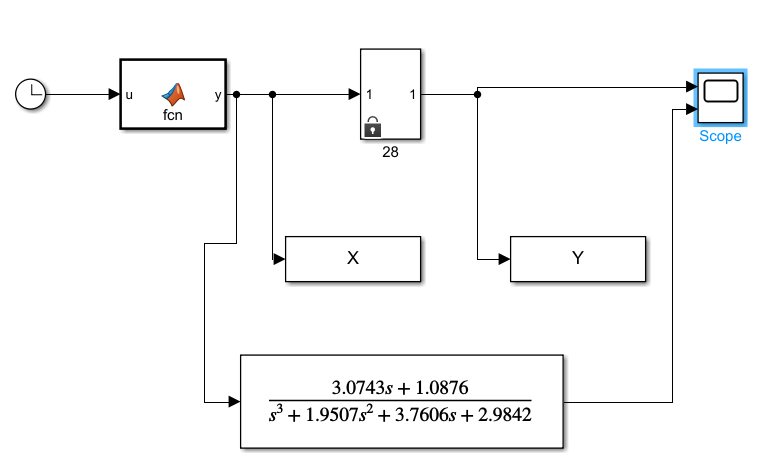 18 Сурет – Объект пен моделдердің шығудағы сигналдарын салыстыру блок-диаграммасы 5.4.11 Нәтижелерін салыстырыңыз. Жұмыс бойынша қорытынды жасаңыз.  19 Сурет – Объект пен моделдердің шығудағы өтпелі процестернің графикттері Менің жаңдайымда 4-ші дәрежелі полином алынды, коэфициенттерін ала отырып функцияны MatLab Command Window жұмыс терезесіне жаздым. Алдымен оны теңдеу ережесі бойынша әр өрнекті дифференциалдап, кейін интегралдадым. Шыққан сан мәндерін сәйкесінше А және В матрицасына жазып жүйенің шешімін алдым, аллынған сандар көмегімен Simulink пакетінде беріліс функциясын құрып, сол бойынша сызбалар бір-біріне жақын болды. Яғни идентификация – объект мен модель арасындағы өзара бір мәнді сәйкестікті орнату процесі. Идентификация – тәжірибелік зерттеулер мәліметтері негізінде объект сипаттамаларын анықтау. Идентификациялау дегеніміз латын тілінен аударғанда ұқсату дегенді білдіреді. ҚорытындыБұл зертханалық жұмыста объектілерді параметрлік идентификациялау, функцияларды аппроксимациялау және сәйкессіздік функционалын минимумдау есептерін шешу әдістерін оқып, білдім. Өзіме берілген нұсқа бойынша объекттің кіріс сигналдың өрнегін жаздым, симулинкте To workspace ұяшығын орнаттым, тәжірибе жүргізу арқылы workspace-те шыққан сан мәнідерін, cftool-ды ашып сонда xdata мен ydata-ға жаздым және де график алдым, сол графикке сәйкес аппроксимациялау полиномының түрін таңдадым. Қисықтарды қиыстыру Curve Fitting Toolbox пакетін қолданып, шығыс сигналды таңдалынған теңдеулермен аппроксимацияладық. Объектінің сызықты динамикалық моделінің құрылымын таңдадық. Таңдалынған құрылым үшін сәйкессіздік функционалының түрін жаздық. Менің жаңдайымда 4-ші дәрежелі полином алынды, коэфициенттерін ала отырып функцияны MatLab Command Window жұмыс терезесіне жаздым. Алдымен оны теңдеу ережесі бойынша әр өрнекті дифференциалдап, кейін интегралдадым. Шыққан сан мәндерін сәйкесінше А және В матрицасына жазып жүйенің шешімін алдым, аллынған сандар көмегімен Simulink пакетінде беріліс функциясын құрып, сол бойынша сызбалар бір-біріне жақын болды. Тәжірибеден алынған мәліметтер негізінде объекттердің регрессиялық модельдерін табуға негізделген статистикалық әдіс – регрессиялық анализ болып табылады. Модельдің белгісіз параметрлері функцияның өлшенген мәндерімен модельден алынған мәндері арасындағы айырымдарының квадраттарының суммасының минимум болатын шарттан табылады. Минималдау есепті шешетін әдіс ең кіші квадраттар әдісі деп аталады. Curve Fitting Toolbox пакеті осы ең кіші квадраттар әдісінде негізделіп қисықтарды қиыстырып келтіреді. Алматы, 2023 |
